
23. Mr. Smith has been here for only a few days, so he hasn’t left a deep impression _____ us.
A. on B. with C. about D. for
22.I don’t think she will come to the meeting on time, ?
A.do I B.do you C.will she D.won’t she
第一节 单项填空(共15小题;每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21. It was so dark that he ______.
A. didn’t dare to go out to fetch some water B. not dared bring some water
C. dares to go out to bring some water D. to dare to fetch some water
2.关于重力势能与重力做功,下列说法中正确的是
A.物体克服重力做的功等于重力势能的增加
B. 在同一高度,将物体以初速度V0向不同的方向抛出到落地过程中,重力做的功相等,物体所减少的重力势能一定相等
C.重力势能等于零的物体,不可能对别的物体做功
D.用手托住一个物体匀速上举时,手的支持力做的功等于克服重力做的功与物体所增加的重力势能之和
⒊一实心的正方体铁块与一实心的正方体木块质量相等,将它们放在水平地面上,下列结论正确的是
A.铁块的重力势能大于木块的重力势能 B铁块的重力势能等于木块的重力势能C.铁块的重力势能小于木块的重力势能 D.上述三种情况都有可能
⒋当物体克服重力做功时,物体的
A重力势能一定减少,机械能可能不变 B重力势能一定增加,机械能一定增加
C重力势能一定增加,动能可能不变 D重力势能一定减少,动能可能减少
[能力训练]
⒈离地面高度(不为零)相同的两物体甲和已,已知M甲>M已,则(以地面为零势面)
A甲物体的势能大 B已物体的势能大
C甲.已两物体的势能相等 D 不能判断
⒉用绳子吊起质量为M的物体,当物体以加速度a匀加速上升H的高度时,物体增加的重力势能为
A MgH B HgH+Mga C M(g-a) D Mga
⒊沿高度相同,坡度不同,粗糙程度也不同的斜面向上拉同一个物体到顶端,在下列说法中正确的是
A沿坡度小,长度大的斜面上升克服重力做的功多
B沿坡度大,粗糙程度大的斜面上升克服重力做的功多
C沿坡度长,粗糙程度大的斜面上升克服重力做的功多
D以上几种情况下克服重力所做的功一样多
⒋如图所示,质量为M的物体静止在地面上,物体上面连着一个轻弹簧,用手拉住弹簧上端将物体缓缓提高H,则人做的功
 A 等于MgH B 大于MgH C
小于MgH
D 无法确定
A 等于MgH B 大于MgH C
小于MgH
D 无法确定
⒌一物体静止在升降机的地板上在升降机加速上升的过程中,地板对物体的支持力所做的功等于
A物体势能的增加量 B 物体动能的增加量
C 物体动能的增加量加上物体势能的增加量
D物体动能的增加量加上克服重力所做的功
⒍质量为100g的球从1.8m的高处落到水平板上,又弹回到1.25m的高度,在整个过程中重力对小球做的功?球的重力势能变化了多少?
⒎地面上平铺N块砖,每块砖的质量为M,厚度为H,如将砖一块一块的叠放起来,至少要做多少功?
 ⒏ 在课本上的实验过程中,如何保证橡皮条第1,第2,第3,……第N次实验时做的功依次为W,2W,3W,……NW?
⒏ 在课本上的实验过程中,如何保证橡皮条第1,第2,第3,……第N次实验时做的功依次为W,2W,3W,……NW?
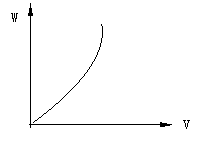
⒐探究实验中若做出的W-V图象,如图所示,怎样
才能证明W∝V2?
0 V
 ⒑如图所示,劲度系数为K1的轻弹簧两端分别与质量为M1和M2的物体栓接,劲度系数为K2的轻弹簧上端与物体M2栓接,下端压在桌面上(不拴接),整个系统处于平衡状态,现施力将物块M1缓缓地竖直上提,直到下面那个弹簧的下端刚脱离桌面,在此过程中,物块M2的重力势能增加了多少?
⒑如图所示,劲度系数为K1的轻弹簧两端分别与质量为M1和M2的物体栓接,劲度系数为K2的轻弹簧上端与物体M2栓接,下端压在桌面上(不拴接),整个系统处于平衡状态,现施力将物块M1缓缓地竖直上提,直到下面那个弹簧的下端刚脱离桌面,在此过程中,物块M2的重力势能增加了多少?
K1
[学后反思]
___________________________________________________________________________
____________________________________________________________________________
_________________________________________________________________
22.(14分)
已知函数f(x)=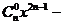


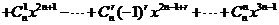 ,
,
其中n .
.
(1)求函数f(x)的极大值和极小值;
(2)设函数f(x)取得极大值时x= ,令
,令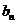 =2
=2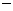 3
3 ,
, =
= ,若p≤
,若p≤ <q对一切n∈N+恒成立,求实数p和q的取值范围.
<q对一切n∈N+恒成立,求实数p和q的取值范围.
21.(12分)
在平面直角坐标系xoy中,点P到M(0,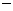
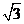 ),N(0,
),N(0,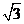 )的距离之和等于4,设点P的轨迹C.
)的距离之和等于4,设点P的轨迹C.
(1)写出曲线C的方程;
(2)设直线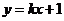 与曲线C交于A、B两点,k为何值时?
与曲线C交于A、B两点,k为何值时?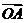
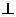
 ,此时
,此时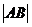 的值是多少?
的值是多少?
20.(12分)
已知 ,若函数,f(x)=
,若函数,f(x)=
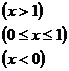 在R上连续.
在R上连续.
求 .
.
19.(12分)
如图,在正方体ABCD - 中E是AB的中点,O是侧面
中E是AB的中点,O是侧面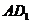 的中心 .
的中心 .
 (1)求证:OB⊥EC ;
(1)求证:OB⊥EC ;
(2)求二面角O-DE-A的大小(用反三角函数表示).
18.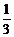
 (12分)射击运动员在双向飞碟射击比赛中,每轮比赛连续发射两枪,击中两个飞靶得2分,击中一个得1分,未击中0分.某运动员在每轮比赛时,第一枪命中率为 ,第二枪命中率为 ,该运动员如进行两轮比赛.
(12分)射击运动员在双向飞碟射击比赛中,每轮比赛连续发射两枪,击中两个飞靶得2分,击中一个得1分,未击中0分.某运动员在每轮比赛时,第一枪命中率为 ,第二枪命中率为 ,该运动员如进行两轮比赛.
(1)求该运动员得4分的概率;
(2)若该运动员所得分数为ξ , 求ξ的分布列及数学期望.
17.(12分)求不等式的解集:
(1) ;
;
(2) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com