
4-1、1997年8月26日在日本举行的国际学术大会上,德国Max Plank学会的一个研究组宣布了他们的研究结果:银河系的中心可能存在一个大“黑洞”,“黑洞”是某些天体的最后演变结果。
(1)根据长期观测发现,距离某“黑洞”6.0×1012m的另一个星体(设其质量为m2)以2×106m/s的速度绕“黑洞”旋转,求该“黑洞”的质量m1。(结果要求两位有效数字)
(2)根据天体物理学知识,物体从某天体上的逃逸速度公式为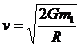 ,其中引力常量G=6.67×10-11N·m2·kg-2,M为天体质量,R为天体半径,且已知逃逸的速度大于真空中光速的天体叫“黑洞”。请估算(1)中“黑洞”的可能最大半径。(结果只要求一位有效数字)
,其中引力常量G=6.67×10-11N·m2·kg-2,M为天体质量,R为天体半径,且已知逃逸的速度大于真空中光速的天体叫“黑洞”。请估算(1)中“黑洞”的可能最大半径。(结果只要求一位有效数字)
解:(1)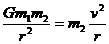 (3分) ∴
(3分) ∴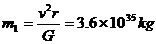 (4分)
(4分)
(2)∵ (3分) ∴
(3分) ∴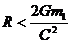 ∴
∴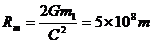 (4分)
(4分)
 4-2、设想宇航员完成了对火星表面的科学考察任务,乘坐返回舱返回围绕火星做圆周运动的轨道舱,如图所示。为了安全,返回舱与轨道舱对接时,必须具有相同的速度。已知返回舱返回过程中需克服火星的引力做功
4-2、设想宇航员完成了对火星表面的科学考察任务,乘坐返回舱返回围绕火星做圆周运动的轨道舱,如图所示。为了安全,返回舱与轨道舱对接时,必须具有相同的速度。已知返回舱返回过程中需克服火星的引力做功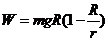 ,返回舱与人的总质量为m,火星表面的重力加速度为g ,火星的半径为R,轨道舱到火星中心的距离为r,不计火星表面大气对返回舱的阻力和火星自转的影响,则该宇航员乘坐的返回舱至少需要获得多少能量才能返回轨道舱?
,返回舱与人的总质量为m,火星表面的重力加速度为g ,火星的半径为R,轨道舱到火星中心的距离为r,不计火星表面大气对返回舱的阻力和火星自转的影响,则该宇航员乘坐的返回舱至少需要获得多少能量才能返回轨道舱?
解:返回舱与人在火星表面附近有: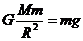 (2分)
(2分)
设轨道舱的质量为m0,速度大小为v,则: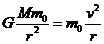 (2分)
(2分)
解得宇航员乘坐返回舱与轨道舱对接时,具有的动能为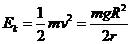 (2分)
(2分)
因为返回舱返回过程克服引力做功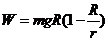
所以返回舱返回时至少需要能量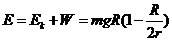 (4分)
(4分)
4-3、2004年,我国现代版的“嫦娥奔月”正式开演,力争2006年12月正式发射。媒体曾报道从卫星图片和美、苏(原苏联)两国勘测结果证明,在月球的永暗面存在着大量常年以固态形式蕴藏的水冰。
但根据天文观测,月球半径为R=1738km,月球表面的重力加速度约为地球表面的重力加速度的1/6,月球表面在阳光照射下的温度可达127℃,此时水蒸气分子的平均速度达到v0=2000m/s。试分析月球表面没有水的原因。(取地球表面的重力加速度g=9.8m/s2)(要求至少两种方法)
解法1:假定月球表面有水,则这些水在127℃时达到的平均速度v0=2000m/s必须小于月球表面的第一宇宙速度,否则这些水将不会降落回月球表面,导致月球表面无水。取质量为m的某水分子,因为GMm/R2=mv12/R2,mg月=GMm/R2,g月=g/6,所以代入数据解得v1=1700m/s,v1<v0,即这些水分子会象卫星一样绕月球转动而不落到月球表面,使月球表面无水。
解法2:设v0=2000m/s为月球的第一宇宙速度,计算水分子绕月球的运行半径R1,如果R1>R,则月球表面无水。取质量为m的某水分子,因为GMm/R12=mv02/R12,mg月=GMm/R12,g月=g/6,所以R1=v02/g月=2.449×106m,R1>R,即以2000m/s的速度运行的水分子不在月球表面,也即月球表面无水。
解法3:假定月球表面有水,则这些水所受到的月球的引力必须足以提供水蒸气分子在月球表面所受到的向心力,即应满足:mg月>GMm/R2,当v=v0=2000m/s时,g月>v02/R=2.30m/s2,而现在月球表面的重力加速度仅为g/6=1.63m/s2,所以水分子在月球表面所受的重力不足以提供2000m/s所对应的向心力,也即月球表面无水。
解法4:假定有水,则这些水所受到的月球的引力必须足以提供水蒸气分子在月球表面所受到的向心力,即应满足:mg月>GMm/R2,,即应有g月R>v2而实际上:g月R=2.84×106m2/s2,v02=4×106m2/s2,所以v02>g月R即以2000m/s的速度运行的水分子不能存在于月球表面,也即月球表面无水。
4-4、物体沿质量为M、半径为R星球的表面做匀速圆周运动所需的速度v1叫做该星球第一宇宙速度;只要物体在该星球表面具有足够大的速度v2,就可以脱离该星球的万有引力而飞离星球(即到达到距星球无穷远处),这个速度叫做该星球第二宇宙速度。理论上可以证明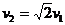 。一旦该星球第二宇宙速度的大小超过了光速C=3.0×108m,则该星球上的任何物体(包括光子)都无法摆脱该星球的引力,于是它就将与外界断绝了一切物质和信息的交流。从宇宙的其他部分看来,它就像是消失了一样,这就是所谓的“黑洞”。
。一旦该星球第二宇宙速度的大小超过了光速C=3.0×108m,则该星球上的任何物体(包括光子)都无法摆脱该星球的引力,于是它就将与外界断绝了一切物质和信息的交流。从宇宙的其他部分看来,它就像是消失了一样,这就是所谓的“黑洞”。
试分析一颗质量为M=2.0×1031kg的恒星,当它的半径坍塌为多大时就会成为一个“黑洞”?(计算时取引力常量G=6.7×10-11Nžm2/kg2,答案保留一位有效数字.)
解: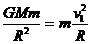 又知
又知 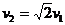 令 v2=C
令 v2=C
由以上三式得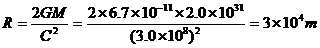
4-5、在美英联军发动的对伊拉克的战争中,美国使用了先进的侦察卫星.据报道,美国有多颗最先进的KH-1、KH-2“锁眼”系列照相侦察卫星可以通过西亚地区上空,“锁眼”系列照相侦察卫星绕地球沿椭圆轨道运动,近地点为265 km(指卫星与地面的最近距离),远地点为650 km(指卫星与地面的最远距离),质量为13.6×103kg-18.2×103kg。这些照相侦察卫星上装有先进的CCD数字照相机,能够分辨出地面上0.l m大小的目标,并自动地将照片传给地面接收站及指挥中心。
由开普勒定律知道:如果卫星绕地球做圆周运动的圆轨道半径与椭圆轨道的半长轴相等,那么卫星沿圆轨道的周期就与其沿椭圆轨道运动的周期相等。请你由上述数据估算这些“锁眼”系列照相侦察卫星绕地球运动的周期和卫星在远地点处的运动速率。地球的半径 R=6 400 km,g取10 m/s2。(保留两位有效数字)
解:设远地点距地面hl,近地点距地面h2,根据题意可知,卫星绕地球做匀速圆周运动的半径 km ① (6分)
km ① (6分)
设卫星绕地球运动的周期为T,根据万有引力定律和牛顿第二定律,有
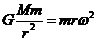 ② (2分)又
② (2分)又 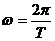 ③ (2分)
③ (2分)
物体在地球表面的重力等于万有引力,则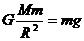 ④ (2分)
④ (2分)
由②③④式可得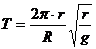 (2分)代入数据可得
(2分)代入数据可得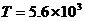 s (2分)
s (2分)
远在点到地面h1,设卫星在远在点的速率为v 则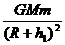 =m
=m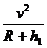 ⑤
⑤
④、⑤联立得 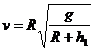 代入数据得 v= 7.6 km/s
代入数据得 v= 7.6 km/s
4-6、一个Internet网站报道,最近南亚某国发射了一颗人造环月卫星,卫星的质量为1000kg,环绕月球周期为60min.张明同学对该新闻的真实性感到怀疑.他认为该国的航天技术不可能近期发射出环月卫星;该网站公布的数据似乎也有问题.他准备对该数据进行验证.但他记不清万有引力恒量的数值,且手边又没有资料可查找,只记得月球半径约为地球半径的1/4,地球半径约为6.4×106m,月球表面的重力加速度约为地球表面重力加速度的1/6,地球表面重力加速度取10m/s2.
假定将环月卫星的运动视为匀速圆周运动,请根据上述数据判断该报道的真伪,并写出推导判断的过程(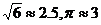 )
)
解:设卫星绕月球表面运行周期为T1,卫星绕地球表面运行周期为T2,月球和地球表面重力加速度分别为g1和g2,月球和地球半径分别为r1和r2
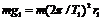 ①
① 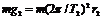 ②
②
①/②得 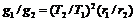 ③
③
由②得 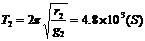 代入③得
代入③得 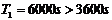
可见不可能发射周期小于6000s的环月卫星。
4-7、目前人们广泛采用GPS全球定位系统导航,这个系统空间星座部分共需要24颗卫星绕地球运转,工作卫星分布在6个圆形轨道面内,每时每刻任何一个地区的地平线上空至少保持4颗卫星传递信息。其对时钟要求精度很高,科学家们采用了原子钟作为计时参照(如:铯原子钟定义的1秒是铯-133原子基态的两个超精细能级之间跃迁所对应的辐射的9192631770个周期所持续的时间,其计时十分精确,10万年内误差不大于1秒),这样导航定位误差可控制在1-2米之内,甚是高明!这种卫星绕地球运行的周期T为12小时,地球半径用R表示,地球表面的重力加速度用g表示,电磁波传播速度用C表示。
(1)这种卫星与地球同步卫星相比较,其轨道高度是高还是低?
(2)这种卫星将电磁信号传于其某时刻地面上的正对点时,所用时间t=?(说明:卫星、地面上该点、地心三点共线,结果用题中所给字母表示)
解:1)这种卫星比地球同步卫星的轨道高度低。4分
(2)万有引力提供向心力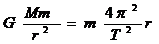 所以
所以 4分
4分
又因为地面附近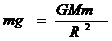 2分 卫星距地面高度
2分 卫星距地面高度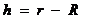 ④2分
④2分
所以时间t=
 ⑤ 4分
⑤ 4分
4-8、2004年1月4日美国“勇气”号火星车在火星表面成功登陆,登陆时间选择在6 万年来火星距地球最近的一次,火星与地球之间的距离仅有5580万千米,火星车在登陆前绕火星做圆周运动,距火星表面高度为H,火星半径为R,绕行N圈的时间为t。求:
(1)若地球、火星绕太阳公转为匀速圆周运动,其周期分别为T地、T火,试比较它的大小;
(2)求火星的平均密度(用R、H、N、t、万有引力常星G表示);
(3)火星车登陆后不断地向地球发送所拍摄的照片,地球上接收到的第一张照片大约是火星车多少秒前拍摄的。
解:1)设环绕天体质量为m,中心天体质量为M。即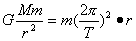 4分
4分
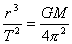
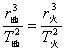 2分 故 T火>T曲 2分
(2)设火星车质量为m设火星质量为M
2分 故 T火>T曲 2分
(2)设火星车质量为m设火星质量为M
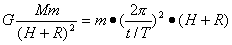 4分
4分
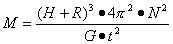 2分
2分
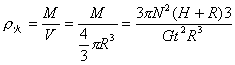 2分
2分
(3)宇宙间用电磁波传输信息:C=3×108m/s
t≈s/v=(5580×107)/(3×108)=186s 4分,是在186秒前拍摄的。
4-9、地球可近视为一个R=6400km的球体,在地面附近的重力加速度g=9.8m/s2,试估算地球的平均密度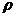 。
。
在古时候,人们通常认为地球是扁平的。想象地球真的不是一个球体,而是一个厚度为H的无限大的盘子,如果想体验与真正地球表面一样的重力加速度,那么H的值是多大?
提示:①假定两种模型地球的密度一样大;
②如果是电荷均匀分布的无限大的这种圆盘(单位面积上的电荷量为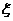 ),圆盘外的电场强度为E=2
),圆盘外的电场强度为E=2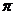 k
k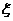 H(k为静电力恒量);
H(k为静电力恒量);
③由电场和重力场类比,它们的对应物理量是:E→g,G→k,m→q;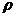 →
→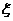 ;
;
④G=6.67×10-11N·m2/kg2
解:1)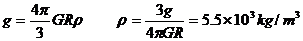
(2)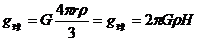 ,
,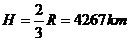
3-1、射地球同步卫星时,可认为先将卫星发射至距地面高度为h1的圆形近地轨道上,在卫星经过A点时点火(喷气发动机工作)实施变轨进入椭圆轨道,椭圆轨道的近地点为A,远地点为B。在卫星沿椭圆轨道(远地点B在同步轨道上),如图14所示。两次点火过程都使卫星沿切向方向加速,并且点火时间很短。已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,求:
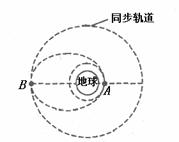 (1)卫星在近地圆形轨道运行接近A点时的加速度大小;
(1)卫星在近地圆形轨道运行接近A点时的加速度大小;
(2)卫星同步轨道距地面的高度。
解:(1)设地球质量为M,卫星质量为m,万有引力常量为G、卫星在近地圆轨道运动接近A点时的加速度为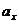 ,根据牛顿第二定律
,根据牛顿第二定律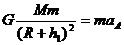 4分
4分
物体在地球表面上受到的万有引力等于重力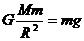 4分
4分
解得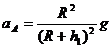 2分
2分
(2)设同步轨道距地面高度h2,根据牛顿第二定律有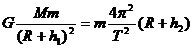 6分
6分
由上式解得: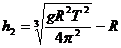 2分
2分

3-2、右图为某报纸的一篇科技报道,你能发现其中的科学性问题吗?请通过必要的计算加以说明。下面的数据在你需要时可选用。
引力常量G=6.7×10-11N·m2/kg2;地球表面重力加速度g=10m/s2;地球半径R=6.4×106m;地球自转周期T=8.6×104s;地球公转周期T'=3.2×107s。(π2=10;70-80的立方根约取4.2)
解:本报道中,地球同步卫星高度735公里的数据出错,以下的计算可以说明。
在地球同步轨道上,卫星受地球的万有引力提供卫星绕地球运转所需的向心力。设卫星的质量为m,离地面高度为h,有: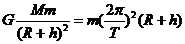
在地球表面上,质量为m0的物体,受地球的万有引力等于物体的重力,有: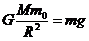
得 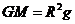 由(1)(2)式可得
由(1)(2)式可得 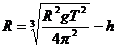
代入数据得 (能说明差2个数量级即可)
(能说明差2个数量级即可)
 2-1、随着我国“神舟五号”宇宙飞船的发射和回收成功。标志着我国的航天技术已达到世界先进水平。如图所示,质量为m的飞船绕地球在圆轨道Ⅰ上运行时,半径为r1,要进入半径为r2的更高的圆轨道Ⅱ,必须先加速进入一个椭圆轨道Ⅲ,然后再进入圆轨道Ⅱ。已知飞船在圆轨道Ⅱ上运动速度大小为υ,在A点通过发动机向后以速度大小为u(对地)喷出一定质量气体,使飞船速度增加到v′进入椭圆轨道Ⅲ。(已知量为:m、r1、r2、υ、v′u)求:
2-1、随着我国“神舟五号”宇宙飞船的发射和回收成功。标志着我国的航天技术已达到世界先进水平。如图所示,质量为m的飞船绕地球在圆轨道Ⅰ上运行时,半径为r1,要进入半径为r2的更高的圆轨道Ⅱ,必须先加速进入一个椭圆轨道Ⅲ,然后再进入圆轨道Ⅱ。已知飞船在圆轨道Ⅱ上运动速度大小为υ,在A点通过发动机向后以速度大小为u(对地)喷出一定质量气体,使飞船速度增加到v′进入椭圆轨道Ⅲ。(已知量为:m、r1、r2、υ、v′u)求:
⑴飞船在轨道I上的速度和加速度大小。
⑵发动机喷出气体的质量△m。
解:(1)在轨道I上,有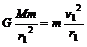 (2分) 解得:
(2分) 解得: (1分)
(1分)
同理在轨道II上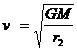 (1分) 由此得:
(1分) 由此得: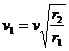 (1分)
(1分)
在轨道I上向心加速度为a1,则有 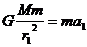 (2分)
(2分)
同理在轨道II上向心加速度a=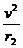 ,则有
,则有 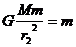
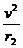 (2分)
(2分)
由此得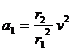 (1分)
(1分)
(2)设喷出气体的质量为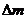 ,由动量守恒得
,由动量守恒得
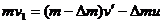 (3分) 得:
(3分) 得: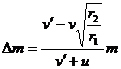 (2分)
(2分)
2-2、2003年10月15日9时整,我国“神舟”五号载人飞船发射成功,飞船绕地球14圈后,于10月16日6时23分安全返回。若把“神舟”五号载人飞船的绕地运行看作是在同一轨道上的匀速圆周运动,已知地球半径为R,地球表面重力加速度为g。
设“神舟”五号载人飞船绕地球运行的周期为T、地球表面的重力加速度为g、地球半径为R,用T、g、R能求出哪些与“神舟”五号载人飞船有关的物理量?分别写出计算这些物理量的表达式(不必代入数据计算)。
解: 对飞船,万有引力作为圆周运动的向心力 ②(2分)
②(2分)
在地球表面 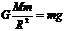 ③
(2分)
③
(2分)
可得“神舟”五号轨道半径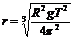 (或轨道周长
(或轨道周长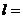
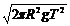 ④
④
此外还可求得“神舟”五号载人飞船的运行频率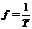 ⑤
⑤
“神舟”五号载人飞船的运行角速度 ⑥
⑥
“神舟”五号载人飞船的运行线速度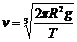 ⑦
⑦
“神舟”五号载人飞船的运行向心加速度(加速度、轨道处重力加速度)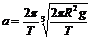 ⑧
⑧
“神舟”五号载人飞船的离地面高度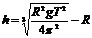 ⑨
⑨
2-3、2003年10月15日,我国神舟五号载人飞船成功发射。标志着我国的航天事业发展到了很高的水平。飞船在绕地球飞行的第5圈进行变轨,由原来的椭圆轨道变为距地面高度为h的圆形轨道。已知地球半径为R,地面处的重力加速度为g.求:
(1)飞船在上述圆轨道上运行的速度v;
(2)飞船在上述圆轨道上运行的周期T.
解:(1)设地球质量为M,飞船质量为m,圆轨道的半径为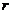
由万有引力定律和牛顿第二定律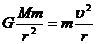 (3分)
(3分)
在地面附近有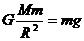 (3分)
由已知条件
(3分)
由已知条件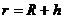 (2分)
(2分)
求出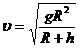 (2分)
(2分)
(2)由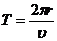 (3分) 求出
(3分) 求出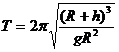 (3分)
(3分)
2-4、国执行首次载人航天飞行的神州五号飞船于2003年10月15日在中国酒泉卫星发 射中心发射升空.飞船由长征-2F运载火箭先送入近地点为A、远地点为B的椭圆轨道,在B点实施变轨后,再进入预定圆轨道,如图所示.已知飞船在预定圆轨道上飞行n圈所用时间为t,近地点A距地面高度为h1,地球表面重力加速度为g,地球半径为R,求:
射中心发射升空.飞船由长征-2F运载火箭先送入近地点为A、远地点为B的椭圆轨道,在B点实施变轨后,再进入预定圆轨道,如图所示.已知飞船在预定圆轨道上飞行n圈所用时间为t,近地点A距地面高度为h1,地球表面重力加速度为g,地球半径为R,求:
(1)飞船在近地点A的加速度aA为多大?
(2)远地点B距地面的高度h2为多少?
解答:(1)设地球质量为M,飞船的质量为m,在A点受到的地球引力为
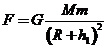 2分
2分
地球表面的重力加速度 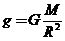 2分
2分
由牛顿第二定律得
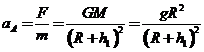 4分
4分
(2)飞船在预定圆轨道飞行的周期  2分
2分
由牛顿运动定律得 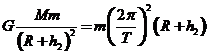 2分
2分
解得 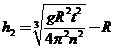 4分
4分
1-1、科学家在地球轨道外侧发现了一颗绕太阳运行的小行星,经过观测该小行星每隔t时间与地球相遇一次,已知地球绕太阳公转半径是R,周期是T,设地球和小行星都是圆轨道,求小行星与地球的最近距离。
解:设小行星绕太阳周期为T/,T/>T,地球和小行星没隔时间t相遇一次,则有
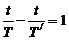
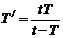
设小行星绕太阳轨道半径为R/,万有引力提供向心力有

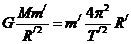
同理对于地球绕太阳运动也有
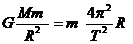
由上面两式有 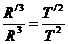
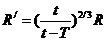
所以当地球和小行星最近时 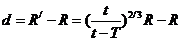
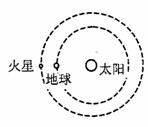 1-2、火星和地球绕太阳的运动可以近似看作为同一平面内同方向的匀速圆周运动,已知火星的轨道半径
1-2、火星和地球绕太阳的运动可以近似看作为同一平面内同方向的匀速圆周运动,已知火星的轨道半径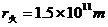 ,地球的轨道半径
,地球的轨道半径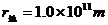 ,从如图所示的火星与地球相距最近的时刻开始计时,估算火星再次与地球相距最近需多少地球年?(保留两位有效数字)
,从如图所示的火星与地球相距最近的时刻开始计时,估算火星再次与地球相距最近需多少地球年?(保留两位有效数字)
解:设行星质量m,太阳质量为M,行星与太阳的距离为r,根据万有引力定律,
行星受太阳的万有引力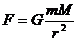 (2分)
(2分)
行星绕太阳做近似匀速圆周运动,根据牛顿第二定律有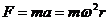 (2分)
(2分)
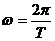 (1分) 以上式子联立
(1分) 以上式子联立 故
故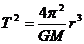 (1分)
(1分)
地球的周期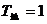 年,(1分)
年,(1分) 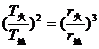 火星的周期
火星的周期 (2分)
(2分)
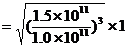 年=1.8年 (1分)
年=1.8年 (1分)
设经时间t两星又一次距离最近,根据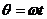 (2分)
(2分)
则两星转过的角度之差 (2分)
(2分)
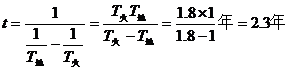 (2分,答“2.2年”同样给分)
(2分,答“2.2年”同样给分)
55.A.lessons B.prizes C.gifts D.subjects
答案 36.B 37.D 38.B 39.C 40.A 41.A 42.D 43.B 44.A 45.C 46.A 47.A 48.C 49.D 50.B 51.D 52.C 53.B 54.A 55.C
54.A.purpose B.pleasure C.position D.progress
53.A.shoulders B.fingers C.arms D.legs
52.A.while B.after C.when D.before
51.A.if B.once C.and D.but
50.A.cared B.mattered C.troubled D.meant
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com