
4.(★★★★)将量程为100μA的电流表改装成量程为1 mA的电流表,并用一标准电流表与改装后的电流表串联,对它进行校准.校准时要求通过电流表的电流能从零连续调到1 mA,试按实验要求画出电路图.
3.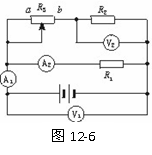 (★★★★)如图12-6所示电路中,电源电动势为E,内电阻为r,R1和R2为定值电阻,R3为可变电阻,当R3的滑动头P由a向b端滑动过程中,电压表V1、V2和电流表A1、A2的读数如何变化?
(★★★★)如图12-6所示电路中,电源电动势为E,内电阻为r,R1和R2为定值电阻,R3为可变电阻,当R3的滑动头P由a向b端滑动过程中,电压表V1、V2和电流表A1、A2的读数如何变化?
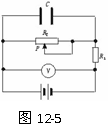
2.(★★★★)如图12-5所示,当变阻器R2的触头P向右滑动时,有
A.电容器C内电场强度增大
B.电压表示数增大
C.R1上消耗的功率增大
D.电源输出的功率一定增大
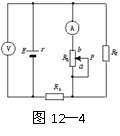
1.(★★★★)(2002年上海)在如图所示12-4所示电路中,当变阻器R3的滑动头P向b端移动时
A.电压表示数变大,电流表示数变小
B.电压表示数变小,电流表示数变大
C.电压表示数变大,电流表示数变大
 D.电压表示数变小,电流表示数变小
D.电压表示数变小,电流表示数变小
2.下列情况可选用限流式接法
(1)测量时电路电流或电压没有要求从零开始连续调节,只是小范围内测量,且RL与R0接近或RL略小于R0,采用限流式接法.
(2)电源的放电电流或滑动变阻器的额定电流太小,不能满足分压式接法的要求时,采用限流式接法.
 (3)没有很高的要求,仅从安全性和精确性角度分析两者均可采用时,可考虑安装简便和节能因素采用限流式接法.
(3)没有很高的要求,仅从安全性和精确性角度分析两者均可采用时,可考虑安装简便和节能因素采用限流式接法.
●歼灭难点训练
滑动变阻器以何种接法接入电路,应遵循安全性、精确性、节能性、方便性原则综合考虑,灵活择取.
1.下列三种情况必须选用分压式接法
(1)要求回路中某部分电路电流或电压实现从零开始可连续调节时(如:测定导体的伏安特性、校对改装后的电表等电路),即大范围内测量时,必须采用分压接法.
(2)当用电器的电阻RL远大于滑动变阻器的最大值R0,且实验要求的电压变化范围较大(或要求测量多组数据)时,必须采用分压接法.因为按图12-3(b)连接时,因RL>>R0>Rap,所以RL与Rap的并联值R并≈Rap,而整个电路的总阻约为R0,那么RL两端电压UL= IR并=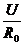 ·Rap,显然UL∝Rap,且Rap越小,这种线性关系越好,电表的变化越平稳均匀,越便于观察和操作.
·Rap,显然UL∝Rap,且Rap越小,这种线性关系越好,电表的变化越平稳均匀,越便于观察和操作.
(3)若采用限流接法,电路中实际电压(或电流)的最小值仍超过RL的额定值时,只能采用分压接法.
图12-3所示的两种电路中,滑动变阻器(最大阻值为R0)对负载RL的电压、电流强度都起控制调节作用,通常把图12-3(a)电路称为限流接法,图12-3(b)电路称为分压接法.
|
|
负载RL上电压调节范围(忽略电源内阻) |
负载RL上电流调节范围(忽略电源内阻) |
相同条件下电路消耗的总功率 |
|
限流接法 |
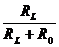 E≤UL≤E E≤UL≤E |
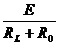 ≤IL≤ ≤IL≤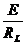 |
EIL |
|
分压接法 |
0≤UL≤E |
0≤IL≤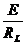 |
E(IL+Iap) |
|
比较 |
分压电路调节范围较大 |
分压电路调节范围较大 |
限流电路能耗较小 |
其中,在限流电路中,通RL的电流IL=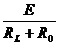 ,当R0>RL时IL主要取决于R0的变化,当R0<RL时,IL主要取决于RL,特别是当R0<<RL时,无论怎样改变R0的大小,也不会使IL有较大变化.在分压电路中,不论R0的大小如何,调节滑动触头P的位置,都可以使IL有明显的变化.
,当R0>RL时IL主要取决于R0的变化,当R0<RL时,IL主要取决于RL,特别是当R0<<RL时,无论怎样改变R0的大小,也不会使IL有较大变化.在分压电路中,不论R0的大小如何,调节滑动触头P的位置,都可以使IL有明显的变化.
7-1、一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下的实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细线直管抡动砝码,使它在竖直平面内做完整的圆周运动,停止抡动细直管。砝码可继续在同一竖直平面内做完整的圆周运动。
如图5所示,此时观察测力计得到当砝码运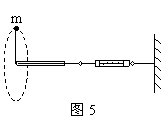 动到圆周的最低点和最高点两位置时,测力计得到当砝码运动到圆周的最低点和最高点两位置时,测力计的读数差为ΔF。
动到圆周的最低点和最高点两位置时,测力计得到当砝码运动到圆周的最低点和最高点两位置时,测力计的读数差为ΔF。
已知引力常量为G,试根据题中所提供的条件和测量结果,求:
(1)该星球表面重力加速度;
(2)该星球的质量M。
解:(1)设最高点 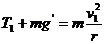 (2分)
最低点
(2分)
最低点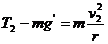 (2分)
(2分)
机械能守恒 (3分)
(3分)
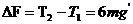 (1分)
(1分)
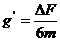 (1分)
(1分)
(2)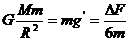 (3分) ∴
(3分) ∴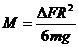 (3分)
(3分)
7-2、宇宙员在月球表面完成下面实验:在一固定的竖直光滑圆弧轨道内部最低点静止一质量为m的小球(可视为质点)如图所示,当施加给小球一瞬间水平冲量I时,刚好能使小球在竖直面内做完整圆周运动.已知圆弧轨道半径为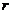 ,月球的半径为R,万有引力常量为G.
,月球的半径为R,万有引力常量为G.
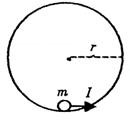 若在月球表面上发射一颗环月卫星,所需最小发射速度为多大?轨道半径为2R的环月卫星周期为多大?
若在月球表面上发射一颗环月卫星,所需最小发射速度为多大?轨道半径为2R的环月卫星周期为多大?
解:设月球表面重力加速度为g,月球质量为M.
在圆孤最低点对小球有:I=mv0……①(2分)
∵球刚好完成圆周运动,∴小球在最高点有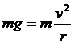 …………②(2分)
…………②(2分)
从最低点至最高低点有: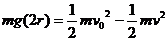 ……③(2分)
……③(2分)
由①②③可得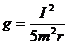 (2分)
(2分)
∵在月球发射卫星的最小速度为月球第一宇宙速度
∴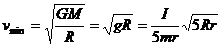 (2分)
(2分)
当环月卫星轨道半径为2R时,有 ……④(2分)
……④(2分)
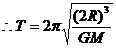 ……⑤(2分)将黄金代换式GM=gR2代入⑤式(2分)
……⑤(2分)将黄金代换式GM=gR2代入⑤式(2分)
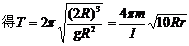 (2分)
(2分)
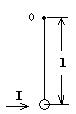 7-3、宇航员在某一星球上以速度
7-3、宇航员在某一星球上以速度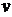
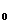 竖直向上抛出一小球,经过时间
竖直向上抛出一小球,经过时间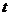 ,小球又落回到原抛出点,然后他用一根长为
,小球又落回到原抛出点,然后他用一根长为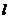 的细绳把一个质量为
的细绳把一个质量为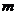 的小球悬挂在o点,使小球处于静止状态。如图所示,现在最低点给小球一个水平向右的冲量
的小球悬挂在o点,使小球处于静止状态。如图所示,现在最低点给小球一个水平向右的冲量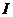 ,使小球能在竖直平面内运动,若小球在运动的过程中始终对细绳有力的作用,则冲量
,使小球能在竖直平面内运动,若小球在运动的过程中始终对细绳有力的作用,则冲量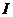 满足什么条件?
满足什么条件?
解:设星球表面附近的重力加速度为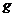 ,由竖直上抛运动公式:
,由竖直上抛运动公式: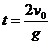 得
得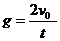 。
。
①当小球摆到与悬点等高处时,细绳刚好松弛,小球对细绳无力作用,则小球在最低点的最小速度为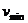 ,由机械能守恒定律得:
,由机械能守恒定律得: 。
。
由动量定理得: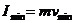 。
。
②当小球做完整的圆周运动时,设最高点的速度为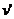 ,由
,由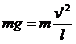 有
有 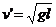 ,若经过最高点细绳刚好松弛,小球对细绳无力作用,则小球在最低点的最大速度为
,若经过最高点细绳刚好松弛,小球对细绳无力作用,则小球在最低点的最大速度为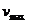 。则由机械能守恒定律和动量定理有:
。则由机械能守恒定律和动量定理有: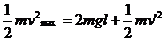 ,
,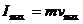 。
。
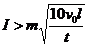 和
和
7-4、2004年1月4日和1月25日,美国“勇气”号和“机遇”号火星车分别登陆火星,同时欧洲的“火星快车”探测器也在环火星轨道上开展了大量科学探测活动。科学家们根据探测器返回的数据进行分析,推测火星表面存在大气,且大气压约为地球表面大气压的1/200,火星直径约为地球的一半,地球的平均密度ρ地=5.5×103kg/m3,火星的平均密度ρ火=4.0×103kg/m3。请根据以上数据估算火星大气质量是地球大气质量的多少倍?(地球和火星表面大气层的厚度均远远小于球体的半径,结果保留两位有效数字)
解:在星球表面物体受到的重力等于万有引力: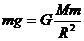
在星球表面: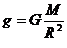 4分
4分
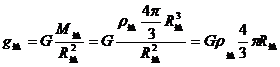 ① 2分
① 2分
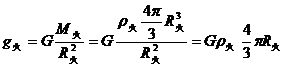 ② 2分
② 2分
由①②得: 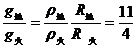 ③ 2分
③ 2分
星球表面大气层的厚度均远远小于星球半径,即大气压强可以表示为:
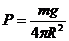 ,得
,得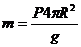 ④ 4分
④ 4分
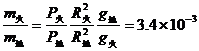 4分
4分
7-5、利用航天飞机,可将物资运送到空间站,也可以维修空间站出现的故障。为完成某种空间探测任务,在空间站上发射的探测器通过向后喷气而获得反冲力使其启动。已知探测器的质量为M,每秒钟喷出的气体质量为m,为了简化问题,设喷射时探测器对气体做功的功率为P,在不长的时间t内探测器的质量变化较小,可以忽略不计。求喷气t秒后探测器获得的动能是多少?
解:由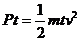 ③ 得
③ 得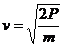 又
又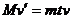 ④
④
得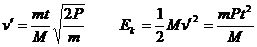
6-1、计划发射一颗距离地面高度为地球半径R0的圆形轨道地球卫星,卫星轨道平面与赤道片面重合,已知地球表面重力加速度为g.
(1)求出卫星绕地心运动周期T
(2)设地球自转周期T0,该卫星绕地旋转方向与地球自转方向相同,则在赤道上一点的人能连续看到该卫星的时间是多少?
解:(1)
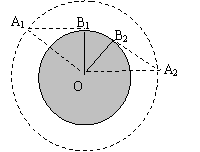
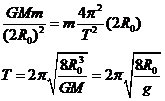
(2)设人在B1位置刚好看见卫星出现在A1位置,最后
在B2位置看到卫星从A2位置消失,OA1=2OB1
有 ∠A1OB1=∠A2OB2=π/3
∠A1OB1=∠A2OB2=π/3
从B1到B2时间为t
则有 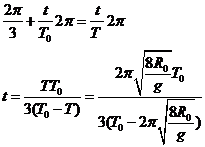
6-2、天文学上,太阳的半径、体积、质量和密度都是常用的物理量,利用小孔成像原理和万有引力定律,可以简捷地估算出太阳的密度。
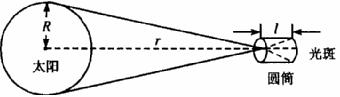
在地面上某处,取一个长l=80cm的圆筒,在其一端封上厚纸,中间扎直径为1mm的圆孔,另一端封上一张画有同心圆的薄白纸,最小圆的半径为2.0mm,相邻同心圆的半径相差0.5mm,当作测量尺度,再用目镜(放大镜)进行观察。把小孔正对着太阳,调整圆筒的方向,使在另一端的薄白纸上可以看到一个圆形光斑,这就是太阳的实像,为了使观察效果明显,可在圆筒的观测端蒙上遮光布,形成暗室。若测得光斑的半径为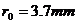 ,试根据以上数据估算太阳的密度(
,试根据以上数据估算太阳的密度(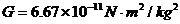 ,一年约为
,一年约为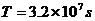 )。
)。
解:设太阳质量为M,半径为R,体积为V,平均密度为ρ,地球质量为m,日地距离为r,由万有引力定律和牛顿运动定律可知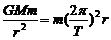 ①(4分)
①(4分)
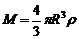 ②(2分)
②(2分)
由图中的几何关系可近似得到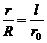 ③(2分)
③(2分)
①②③联立解得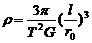 ④(3分)代入数据得:
④(3分)代入数据得: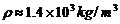 ⑤(1分)
⑤(1分)
6-3、某颗同步卫星正下方的地球表面上有一观察者,用天文望远镜观察到被太阳光照射的该同步卫星。试问秋分这一天(太阳光直射赤道)从日落时起经过多长时间,观察者恰好看不见该卫星。已知地球半径为R,地球表面处重力加速度为g,地球自转周期为T。不考虑大气对光的折射
解:M表示球的质量,m表示同步卫星的质量,r表示同表卫星距地心的距离。
 对同步卫星:
对同步卫星: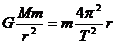
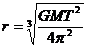 4分
4分
对地表面上一物体: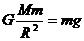 GM=gR2 3分
GM=gR2 3分
由图得: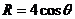 3分
3分
又由图: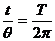 3分
3分
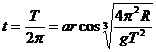 3分
3分
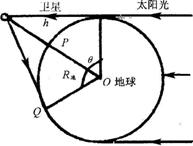 6-4、晴天晚上,人能看见卫星的条件是卫星被太阳照着且在人的视野之内。一个可看成漫反射体的人造地球卫星的圆形轨道与赤道共面,卫星自西向东运动。春分期间太阳垂直射向赤道,赤道上某处的人在日落后8小时时在西边的地平线附近恰能看到它,之后极快地变暗而看不到了。已知地球的半径
6-4、晴天晚上,人能看见卫星的条件是卫星被太阳照着且在人的视野之内。一个可看成漫反射体的人造地球卫星的圆形轨道与赤道共面,卫星自西向东运动。春分期间太阳垂直射向赤道,赤道上某处的人在日落后8小时时在西边的地平线附近恰能看到它,之后极快地变暗而看不到了。已知地球的半径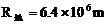 ,地面上的重力加速度为
,地面上的重力加速度为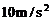 ,估算:(答案要求精确到两位有效数字)
,估算:(答案要求精确到两位有效数字)
(1)卫星轨道离地面的高度。
(2)卫星的速度大小。
解:从北极沿地轴往下看的地球俯视图如图所示,设卫星离地高h,Q点日落后8小时时能看到它反射的阳光。日落8小时Q点转过的角度设为θ
(1)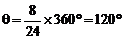
轨道高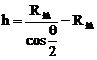
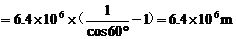
(2)因为卫星轨道半径
根据万有引力定律,引力与距离的平方成反比
卫星轨道处的重力加速度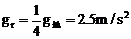
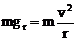
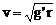
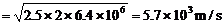 (
(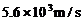 同样给分)
同样给分)
5-1、现根据对某一双星系统的光学测量确定,该双星系统中每个星体的质量都是M,两者相距L,它们正围绕两者连线的中点做圆周运动。万有引力常量为G。求:
(1)试计算该双星系统的运动周期T。
(2)若实验上观测到运动周期为T’,且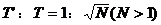 ,为了解释两者的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的物质--暗物质,作为一种简化的模型,我们假定在以这两个星体连线为直径的球体内均匀分布着这种暗物质,而不考虑其他暗物质的影响,试根据这一模型和上述观测结果确定该星系间这种暗物质的密度。
,为了解释两者的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的物质--暗物质,作为一种简化的模型,我们假定在以这两个星体连线为直径的球体内均匀分布着这种暗物质,而不考虑其他暗物质的影响,试根据这一模型和上述观测结果确定该星系间这种暗物质的密度。
解:(1)由万有引力提供向心力有: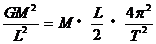 ①(4分)
①(4分)
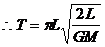 (4分)
(4分)
(2)设暗物的密度为ρ,质量为m,则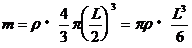 (2分)
(2分)
由万有引力提供向心力有: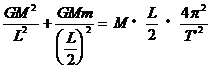 ②(2分)
②(2分)
由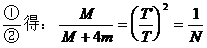 (2分)
(2分)
又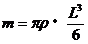 代入上式解得:
代入上式解得: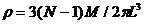 (2分)
(2分)
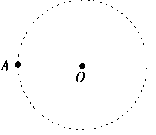
5-2、如图为宇宙中有一个恒星系的示意图。A为星系的一颗行星,它绕中央恒星O运行的轨近似为圆。天文学家观测得到A行星运动的轨道半径为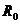 、周期为
、周期为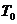 。
。
 经长期观测发现,A行星实际运动的轨道与圆轨道总存在一些偏离,且周期性地每隔
经长期观测发现,A行星实际运动的轨道与圆轨道总存在一些偏离,且周期性地每隔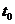 时间发生一次最大的偏离。天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知的行星B(假设其运行轨道与A在同一水平面内,且与A的绕行方向相同),它对A行星的万有引力引起A轨道的偏离。根据上述现象及假设,你能对未知行星B的运动得到哪些定量的预测?
时间发生一次最大的偏离。天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知的行星B(假设其运行轨道与A在同一水平面内,且与A的绕行方向相同),它对A行星的万有引力引起A轨道的偏离。根据上述现象及假设,你能对未知行星B的运动得到哪些定量的预测?
解: A行星发生最大偏离时,A、B行星与恒星在同一直线上且位于恒星同一侧。设行星B的运行周期为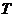 、半径为
、半径为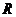 ,则有
,则有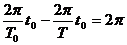 ,所以
,所以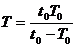 由开普勒第三定律得,
由开普勒第三定律得, ,所以
,所以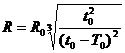
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com