
14.(2009浙江卷理)观察下列等式:
 ,
,
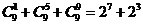 ,
,
 ,
,
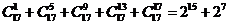 ,
,
………
由以上等式推测到一个一般的结论:
对于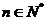 ,
,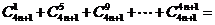 .
. 

答案 
解析 这是一种需类比推理方法破解的问题,结论由二项构成,第二项前有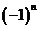 ,
,
二项指数分别为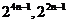 ,因此对于
,因此对于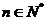 ,
,
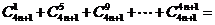

13.(2009四川卷理) 的展开式的常数项是
(用数字作答)
的展开式的常数项是
(用数字作答)
[考点定位]本小题考查二项式展开式的特殊项,基础题。(同文13)
解析 由题知 的通项为
的通项为 ,令
,令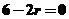 得
得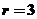 ,故常数项为
,故常数项为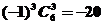 。
。
12.(2009湖南卷理)在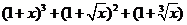 的展开式中,
的展开式中,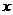 的系数为___7__(用数
的系数为___7__(用数
字作答)
答案 7 

解析 由条件易知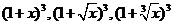 展开式中
展开式中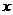 项的系数分别是
项的系数分别是 ,即所求系数是
,即所求系数是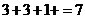
11.(2009四川卷文) 的展开式的常数项是
(用数字作答)
的展开式的常数项是
(用数字作答)
m 答案 -20
解析  ,令
,令 ,得
,得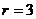
故展开式的常数项为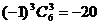
10.(2009全国卷Ⅰ文)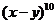 的展开式中,
的展开式中,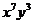 的系数与
的系数与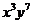 的系数之和等于________.
的系数之和等于________.
解析 本小题考查二项展开式通项、基础题。(同理13)
解: 因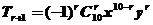 所以有
所以有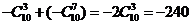
9.(2009湖南卷文)在 的展开式中,
的展开式中,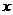 的系数为 6 (用数字作答).
的系数为 6 (用数字作答).
解: 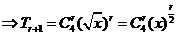 ,故
,故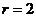 得
得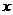 的系数为
的系数为
7.(2009重庆卷文)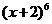 的展开式中
的展开式中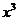 的系数是( )
的系数是( )


A.20 B.40 C.80 D.160
答案 D
解法1设含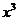 的为第
的为第 ,则
,则
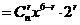 ,令
,令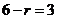 ,得
,得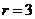 ,故展开式中
,故展开式中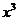 的系数为
的系数为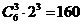 。
。
解法2根据二项展开式的通过公式的特点:二项展开式每一项中所含的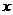 与2分得的次数和为6,则根据条件满足条件
与2分得的次数和为6,则根据条件满足条件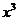 的项按3与3分配即可,则展开式中
的项按3与3分配即可,则展开式中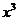 的系数为
的系数为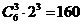 。8.(2009重庆卷理)
。8.(2009重庆卷理) 的展开式中
的展开式中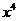 的系数是( )
的系数是( )
A.16 B.70 C.560 D.1120
答案
解析 设含 的为第
的为第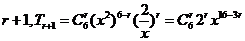 ,
,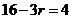
所以 ,故系数为:
,故系数为: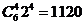 ,选D。
,选D。
6.(2009陕西卷文)若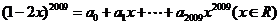 ,则
,则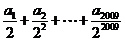 的值为
的值为
A. 2 B.0 C. D.
D. 

答案
C 

解析 由题意容易发现
 ,则
,则
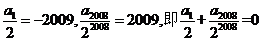 , 同理可以得出
, 同理可以得出
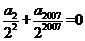 ,
,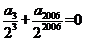 ………
………
亦即前2008项和为0, 则原式=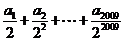 =
=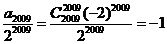 故选C.
故选C.
5.(2009湖北卷理)设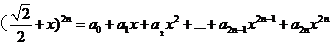 ,则
,则

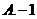
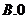


答案 B
解析
令 得
得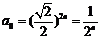
令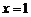 时
时
令 时
时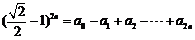
两式相加得: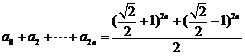
两式相减得: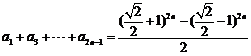
代入极限式可得,故选B
4.(2009江西卷理)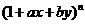 展开式中不含
展开式中不含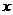 的项的系数绝对值的和为
的项的系数绝对值的和为 ,不含
,不含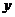 的项的系数绝对值的和为
的项的系数绝对值的和为 ,则
,则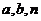 的值可能为
的值可能为
A. B.
B.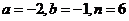
C. D.
D.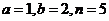


答案 D
解析 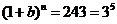 ,
,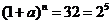 ,则可取
,则可取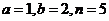 ,选D
,选D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com