6.夹在互相垂直的两个平面之间长为2a的线段和这两个平面所成的角分别为45°和30°，过这条线段的两个端点分别向这两个平面的交线作垂线，则两垂足间的距离为_____________.

◆答案提示：1-4.CBBB；

5．如图在四棱锥P-ABCD中，PA⊥底面ABCD，底面各边都相等，M是PC上的一动点，当点M满足__________时，平面MBD⊥平面PCD.

4.P为△ABC所在平面外的一点，则点P在此三角形所在平面上的射影是△ABC垂心的充分必要条件是

A.PA=PB=PC　　 B.PA⊥BC，PB⊥AC　 (　 )

C.点P到△ABC三边所在直线距离相等

D.平面PAB、平面PBC、平面PAC与△ABC所在的平面所成的角相等

3.设两个平面α、β，直线l ，下列三个条件：① l ⊥α; ② l∥β;③α⊥β,若以其中两个作为条件，另一个作为结论，可构成正确命题的个数是　　 　　(　 )

A.3　　 B.2　　　 C. 1　　 D. 0

2.设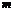、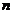是两条不同的直线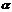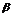，、是两个不同的平面.考查下列命题，其中正确的命题是　　　 (　 )　　　　　

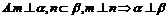
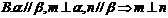
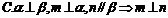
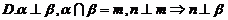
1.在三棱锥A-BCD中，若AD⊥BC，BD⊥AD，△BCD是锐角三角形，那么必有(　 )

A.平面ABD⊥平面ADC　　　　　

B.平面ABD⊥平面ABC

C.平面ADC⊥平面BCD　　　

　　 D.平面ABC⊥平面BCD

3．二面角的平面角的作法：

①直接利用定义；

②利用三垂线定理及其逆定理;

③作棱的垂面.

2．判定两平面垂直的方法：

①利用“面面垂直的定义”，即证“两平面所成的二面角是直二面角；

②利用“面面垂直的判定定理”，即由“线面垂直Þ面面垂直”.

1.二面角、平面角的定义--；

范围：.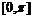

两个平面相交成90⁰二面角时，叫两个平面垂直.

3．在研究垂直和求二面角的问题时，要能灵活运用三垂线定理及逆定理