
5.(2005浙江)设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.
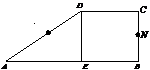

4.设a、b是异面直线,α、β是两个平面,且a⊥α,b⊥β,a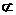 β,b
β,b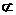 α,则当_______(填上一种条件即可)时,有α⊥β.
α,则当_______(填上一种条件即可)时,有α⊥β.
3.在1200的二面角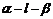 内,有一点P到面α、β的距离分别是6和9 ,则点P到棱l的距离等于
( )
内,有一点P到面α、β的距离分别是6和9 ,则点P到棱l的距离等于
( )
A.3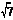 B.
B. 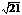 C.
2
C.
2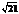 D. 12
D. 12
[填空题]
2.在边长为a的正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=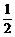 a,且二面角B-AD-C的大小为
( )
a,且二面角B-AD-C的大小为
( )
A.30° B.45° C.60° D.90°
1. PA垂直于以AB为直径的圆所在的平面,C为圆上异于A、B的任一点,则下列关系不正确的是 ( )
A PA⊥BC B AC⊥PB
C PC⊥BC D BC⊥平面PAC
3.作平面角的方法:(1)定义法
(2)三垂线定理; (3)垂面法 .
同步练习 9.4二面角、面面垂直
[选择题]
2.求二面角的方法是:
①找(或作)平面角,②用射影法: cosθ=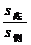 ;
;
③用异面直线上两点间距离公式.
1. 注意线线垂直、线面垂直、面面垂直之间的转化和应用.
注意线线垂直、线面垂直、面面垂直之间的转化和应用.
[例1] 如下图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.
(1)求证:AB⊥BC;
(2)若设二面角S-BC-A为45°,SA=BC,求二面角A-SC-B的大小.
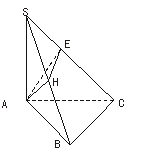

证明(1):作AH⊥SB于H,
∵平面SAB⊥平面SBC,
∴AH⊥平面SBC. 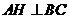 ,又SA⊥平面ABC,
,又SA⊥平面ABC,
∴SA⊥BC.SA∩SB=S,
∴BC⊥平面SAB. ∴BC⊥AB.
解(2):∵SA⊥平面ABC,∴SA⊥BC.
∴平面SAB⊥BC,∠SBA为二面角S-BC-A的平面角.
∴∠SBA=45°.设SA=AB=BC=a.作AE⊥SC于E,连结EH.
由(1)知AH⊥平面SBC, ∴AE在面SBC内的射影EH⊥SC,∠AEH为二面角A-SC-B的平面角,
AH=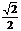 a,AC=
a,AC=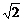 a,SC=
a,SC=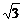 a,AE=
a,AE=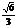 a,
a,
∴sin∠AEH=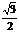 ,二面角A-SC-B为60°.
,二面角A-SC-B为60°.
[例2] 已知正三棱柱ABC-A1B1C1,若过面对角线AB1且与另一面对角线BC1平行的平面交上底面A1B1C1的一边A1C1于点D.
(1)确定D的位置,并证明你的结论;
(2)证明:平面AB1D⊥平面AA1D;
(3)若AB∶AA1=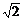 ,求平面AB1D与平面AB1A1所成角的大小.
,求平面AB1D与平面AB1A1所成角的大小.
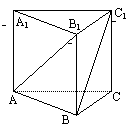

分析:本题结论不定,是“开放性”的,点D位置的确定如果仅凭已知条件推理难以得出.由于AB1与BC1这两条面对角线是相邻二侧面上的异面直线,于是可考虑将BC1沿BA平行移动,BC1取AE1位置,则平面AB1E1一定平行BC1,问题可以解决.
(1)解:如下图,将正三棱柱ABC-A1B1C1补成一直平行六面体ABCE-A1B1C1E1,由AE1∥BC1,AE1 平面AB1E1,知BC1∥平面AB1E1,故平面AB1E1应为所求平面,此时平面AB1E1交A1C1于点D,由平行四边形对角线互相平行性质知,D为A1C1的中点.
平面AB1E1,知BC1∥平面AB1E1,故平面AB1E1应为所求平面,此时平面AB1E1交A1C1于点D,由平行四边形对角线互相平行性质知,D为A1C1的中点.
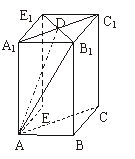

(2)证明:连结B1D,则B1D⊥A1C1;从直三棱柱定义知AA1⊥底面A1B1C1,
∴AA1⊥B1D, 又A1D∩AA1=A1,
∴B1D⊥平面AA1D,又B1D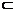 平面AB1D,
平面AB1D,
∴平面AB1D⊥平面AA1D.
(3)解:因为平面AB1D∩平面AA1D=AD,所以过A1作A1H⊥AD于点H.作HF⊥AB1于点F,连结A1F,从三垂线定理知A1F⊥AB1.
故∠A1FH是二面角A1-AB1-D的平面角.
设侧棱AA1=1,侧棱AB=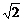 .
.
于是AB1=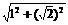 =
= 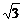 .
.
在Rt△AB1A1中,A1F=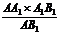 =
=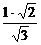 =
=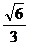 ,
,
在Rt△AA1D中,AA1=1,A1D= A1C1=
A1C1=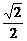 ,
,
AD=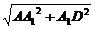 =
= 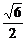 .
.
∴A1H=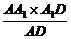 =
=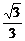 .
.
在Rt△A1FH中,sin∠A1FH=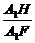 =
=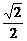 ,∴∠A1FH=45°.
,∴∠A1FH=45°.
因此知平面AB1D与平面AB1A1所成角为450或1350.
[例3]在四棱锥P-ABCD中,已知ABCD为矩形,PA ⊥平面ABCD,设PA=AB=1,BC=2,求二面角B-PC-D的大小.
解析1.定义法 过D作DE ⊥PC于E,
过E作EF ⊥PC,交BC于F,连接
FD,则 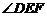 是所求二面角B-PC-D
是所求二面角B-PC-D
的平面角.求解二面角B-PC-D的大小,只需解△DEF即可.所求角为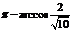
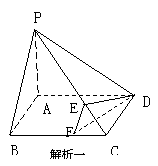

解析2.垂面法 易证面PAB⊥面PBC,过A作AM ⊥BP于M,显然AM ⊥面PBC,从而有AM ⊥PC,同法可得AN ⊥PC,再由AM与AN相交与A得PC ⊥面AMN.设面AMN交PC于Q,
则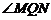 为二面角B-PC-D的平面角;
为二面角B-PC-D的平面角;
∠MAN为它的补角,在三角形AMN中可解.计算较繁.
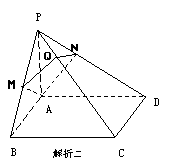


 解析3.利用三垂线求解把四棱锥P-ABCD补成如图的直三棱柱PAB-EDC,显然二面角E-PC-D与二面角D-PC-B互补,转化为求二面角E-PC-D.
解析3.利用三垂线求解把四棱锥P-ABCD补成如图的直三棱柱PAB-EDC,显然二面角E-PC-D与二面角D-PC-B互补,转化为求二面角E-PC-D.
易证面PEDA ⊥PDC,过E作EF ⊥ PD
于F,显然PF ⊥面PDC,在面PCE内,
过E作EG ⊥PC于G,连接GF,由三
线得GF⊥
PC 即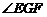 为二面角E-PC-D的平面角,只需解△EFG即可.
为二面角E-PC-D的平面角,只需解△EFG即可.

解析4. 射影面积法。由解析3知,△PFC为△ PEC
在面PDC上的射影,由射影面积公式得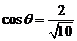 ,所求角为
,所求角为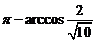

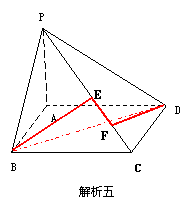
解析5.在面PDC内,分别过D、B作DE ⊥PC于E,BF ⊥PC于F,连接EF即可.利用平面知识求BF、EF、DE的长度,再利用空间余弦定理求出q 即可.

◆思悟提炼:想一想求二面角都用了哪些方法:
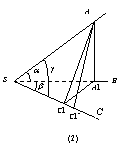
[例4]由一点S引不共面的三条射线SA、SB、SC,设ÐASB=a,ÐBSC=b,ÐASC=g,其中a,b,g均为锐角,则平面ASB^平面BSC的充要条件是cosa×cosb=cosg.
证明:必要性.如图(1), 过点A作AD^SB于D.
∵平面ASB^平面BSC, ∴AD^平面BSC.
过D作DE^SC于E,连AE,则AE^SC.
在Rt△ADS中,cosa=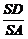 ;
;
在Rt△DES中,cosb=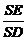 ;
;
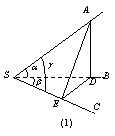

例3. |
在Rt△AES中,cosg=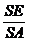 ,由此可得
,由此可得
cosa×cosb=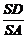 ×
×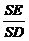 =
=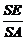 =cosg.
必要性得证.
=cosg.
必要性得证.
充分性.如图2,过点A作AA1^SB于A1,过点A1作A1C1^SC于C1.
在Rt△AA1S中,cosa=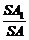 ;
;
在Rt△A1C1S中,cosb=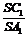 ;
;
∵cosg=cosa×cosb=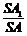 ×
×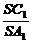 =
=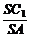 ,
,
∴SC1=SA×cosg.

过A作AC1¢^SC,垂足为C1¢,在Rt△AC1¢S中,SC1¢=SA×cosg.
由此得SC1¢=SC1,即C1¢与C1重合,故SC^AC1.
而SC^A1C1,且AC1IA1C1=C1,
∴SC^平面AA1C1,∴SC^AA1.
又∵SB^AA1,SBISC=S,
∴AA1^平面BSC,而AA1Ì平面ASB,
∴平面ASB^平面BSC.充分性得证.
5. MD⊥PC或MB⊥PC ; 6. a
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com