
15. (06北京理综22)右图是简化后的跳台滑雪的雪道示意图.整个雪道由倾斜的助滑雪道AB和着陆雪道DE,以及水平的起跳平台CD组成,AB与CD圆滑连接。动员从助滑雪道AB上由静止开始,在重力作用下,滑到D点水平飞出,不计飞行中的空气阻力,经2 s在水平方向飞行了60 m,落在着陆雪道DE上.已知从B点到D点运动员的速度大小不变.(g取10 m/s2)求:
(06北京理综22)右图是简化后的跳台滑雪的雪道示意图.整个雪道由倾斜的助滑雪道AB和着陆雪道DE,以及水平的起跳平台CD组成,AB与CD圆滑连接。动员从助滑雪道AB上由静止开始,在重力作用下,滑到D点水平飞出,不计飞行中的空气阻力,经2 s在水平方向飞行了60 m,落在着陆雪道DE上.已知从B点到D点运动员的速度大小不变.(g取10 m/s2)求:
(1)运动员在AB段下滑到B点的速度大小.
(2)若不计阻力,运动员在AB段下滑过程中下降的高度.
答案 (1)30 m/s (2)45 m ?
解析 (1)运动员从D点飞出时的速度
v=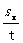 =30
m/s?
=30
m/s?
依题意,下滑到助滑雪道末端B点的速度大小是30 m/s?.
(2)在下滑过程中机械能守恒,有
mgh= mv2 下降的高度h=
mv2 下降的高度h= =45
m?
=45
m?
题组二
14.(06全国卷Ⅱ23)如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=0.5 m,轨道在C处与水平地面相切,在C处放一小物块,给它一水平向左的初速度v0=5 m/s,结果它沿CBA运动,通过A点,最后落在水平地面上的D点,求C、D间的距离s.取重力加速度g=10 m/s2.

答案 1 m
解析 设小物块的质量为m,过A处时的速度为v,由A到D经历的时间为t,有
 mv02=
mv02= mv2+2mgR ①
mv2+2mgR ①
2R= gt2 ②
gt2 ②
s=vt ③
由①②③式并代入数据得s=1 m?
13.(06广东15)一个质量为4 kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1.从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示.求83秒内物体的位移大小和力F对物体所做的功(g取10 m/s2).

答案 167 m 676 J
解析 第1个2s内,其加速度:
a1= =
= m/s2=2 m/s2
m/s2=2 m/s2
第1个2 s末的速度:
v1=a1t=2×2 m/s=4 m/s?
第1个2 s内的位移:
s1= ?
?
第2个2 s内做减速运动,其加速度大小:
a2=
第2个2 s末的速度:v2=v1-a2t=0
第2个2 s内的位移:s2= ?
?
故物体先匀加速2 s达最大速度4 m/s,后又匀减速运动2 s速度变为零,以后将重复这个运动.
前84 s内物体的位移s=21(s1+s2)=168 m?
最后1 s内物体的位移s′=
故83秒内物体的位移为168 m-1 m=167 m?
第83秒末的速度与第3秒末的速度相等,故v=v1
所以力F对物体所做的功W= mv2+fs83=8
J+668 J=676 J?
mv2+fs83=8
J+668 J=676 J?
12.(07天津理综23)如图所示,水平光滑地面上停放着一辆小车,左侧靠在竖直墙壁上,小车的四分之一圆弧轨道AB是光滑的,在最低点B与水平轨道BC相切,BC的长度是圆弧半径的10倍,整个轨道处于同一竖直平面内.可视为质点的物块从A点正上方某处无初速下落,恰好落入小车圆弧轨道滑动.然后沿水平轨道滑行至轨道末端C处恰好没有滑出.已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍,小车的质量是物块的3倍,不考虑空气阻力和物块落入圆弧轨道时的能量损失.求:
(1)物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的几倍.
(2)物块与水平轨道BC间的动摩擦因数μ.

答案 (1)4倍 (2)0.3
解析 (1)设物块的质量为m,其开始下落处的位置距BC的竖直高度为h,到达B点时的速度为v,小车圆弧轨道半径为R.由机械能守恒定律,有
mgh= mv2 ①
mv2 ①
根据牛顿第二定律,有
9mg-mg=m ②
②
解得h=4R ③
即物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的4倍.
(2)设物块与BC间的滑动摩擦力的大小为F,物块滑到C点时与小车的共同速度为v′,物块在小车上由B运动到C的过程中小车对地面的位移大小为s.依题意,小车的质量为3m,BC长度为10 R.由滑动摩擦定律,有
F=μmg ④
由动量守恒定律,有mv=(m+3m)v′ ⑤
对物块、小车分别应用动能定理,有
-F(10R+s)= mv′2-
mv′2- mv2 ⑥
mv2 ⑥
Fs= (3m)v′2-0 ⑦
(3m)v′2-0 ⑦
解得μ=0.3 ⑧
11.(07全国卷Ⅱ23)如图所示,位于竖直平面内的光滑轨道,由一段斜的直轨道和与之相切的圆形轨道连接而成,圆形轨道的半径为R.一质量为m的小物块从斜轨道上某处由静止开始下滑,然后沿圆形轨道运动.要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能超过5mg(g为重力加速度).求物块初始位置相对于圆形轨道底部的高度h的取值范围。

答案  R≤h≤5R
R≤h≤5R
解析 设物块在圆形轨道最高点的速度为v,由机械能守恒定律得
mgh=2mgR+ mv2 ①
mv2 ①
物块在最高点受的力为重力mg、轨道的压力N.重力与压力的合力提供向心力,有
mg+N=m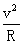 ②
②
物块能通过最高点的条件是
N≥0 ③
由②③式得
v≥ ④
④
由①④式得
h≥ R ⑤
R ⑤
按题目要求,N≤5 mg,由②式得
v≤ ⑥
⑥
由①⑥式得
h≤5R ⑦
h的取值范围是
 R≤h≤5R ⑧
R≤h≤5R ⑧
10.(07江苏19)如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环.棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg(k>1).断开轻绳,棒和环自由下落.假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失.棒在整个运动过程中始终保持竖直,空气阻力不计.求:
(1)棒第一次与地面碰撞弹起上升过程中,环的加速度.
(2)从断开轻绳到棒与地面第二次碰撞的瞬间,棒运动的路程s.
(3)从断开轻绳到棒和环都静止,摩擦力对环及棒做的总功W.

答案 (1)(k-1)g,方向竖直向上 (2)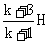 (3)-
(3)-
解析 (1)设棒第一次上升过程中,环的加速度为a环
环受合力F环=kmg-mg ①
由牛顿第二定律F环=ma环 ②
由①②得a环=(k-1)g,方向竖直向上
(2)设以地面为零势能面,向上为正方向,棒第一次落地的速度大小为v1.
由机械能守恒得: ×2mv12=2mgH
×2mv12=2mgH
解得v1=
设棒弹起后的加速度a棒
由牛顿第二定律a棒=-(k+1)g
棒第一次弹起的最大高度H1=-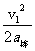
解得H1=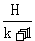
棒运动的路程s=H+2H=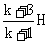
(3)解法一:棒第一次弹起经过t1时间,与环达到相同速度v1′
环的速度v1′=-v1+a环t1
棒的速度v1′=v1+a棒t1
环的位移h环1=-v1t1+ a环t12
a环t12
棒的位移h棒1=v1t1+ a棒t12
a棒t12
x1=h环1-h棒1?
解得:x1=-
棒环一起下落至地
v22-v1′2=2gh棒1?
解得:v2=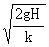
同理,环第二次相对棒的位移
x2=h环2-h棒2=-
……
xn=-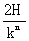
环相对棒的总位移
x=x1+x2+……+xn+……
W=kmgx
得W=-
解法二:设环相对棒滑动距离为l
根据能量守恒mgH+mg(H+l)=kmgl
摩擦力对棒及环做的总功
W=-kmgl
解得W=-
9.(07山东理综)如图所示,一水平圆盘绕过圆心的竖直轴转动,圆盘边缘有一质量m=1.0 kg的小滑块.当圆盘转动的角速度达到某一数值时,滑块从圆盘边缘滑落,经光滑的过渡圆管进入轨道ABC.已知AB段斜面倾角为53°,BC段斜面倾角为37°,滑块与圆盘及斜面间的动摩擦因数均为μ=0.5,A点离B点所在水平面的高度h=1.2 m.滑块在运动过程中始终未脱离轨道,不计在过渡圆管处和B点的机械能损失,最大静摩擦力近似等于滑动摩擦力,取g=10 m/s2,sin 37°=0.6,cos 37°=0.8.
(1)若圆盘半径R=0.2 m,当圆盘的角速度多大时,滑块从圆盘上滑落?
(2)若取圆盘所在平面为零势能面,求滑块到达B点时的机械能.
(3)从滑块到达B点时起,经0.6 s正好通过C点,求BC之间的距离.

答案 (1)5 rad/s (2)-4 J (3)0.76 m
解析 (1)滑块在圆盘上做圆周运动时,静摩擦力充当向心力,根据牛顿第二定律,可得:
μmg=mω2R
代入数据解得:ω= =5
rad/s?
=5
rad/s?
(2)滑块在A点时的速度:vA=ωR=1 m/s?
从A到B的运动过程由动能定理得
mgh-μmgcos 53° · =
= mvB2-
mvB2- mvA2
mvA2
在B点时的机械能:EB= mvB2-mgh=-4
J
mvB2-mgh=-4
J
(3)滑块在B点时的速度:vB=4 m/s?
滑块沿BC段向上运动时的加速度大小:
a1=g(sin 37°+μcos 37°)=10 m/s2
返回时的加速度大小
a2=g(sin 37°-μcos 37°)=2 m/s2
BC间的距离:sBC= =0.76
m
=0.76
m
8.(07上海5)在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+ π)(单位: m),式中k=1 m-1.将一光滑小环套在该金属杆上,并从x=0处以v0=5 m/s的初速度沿杆向下运动,取重力加速度g=10 m/s2..则当小环运动到x=
π)(单位: m),式中k=1 m-1.将一光滑小环套在该金属杆上,并从x=0处以v0=5 m/s的初速度沿杆向下运动,取重力加速度g=10 m/s2..则当小环运动到x= m时的速度大小v=
m/s;该小环在x轴方向最远能运动到x=
m处. 答案
m时的速度大小v=
m/s;该小环在x轴方向最远能运动到x=
m处. 答案 
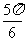

解析 当x=0时,y1=2.5 cos  π=-1.25
m,当x=
π=-1.25
m,当x= 时,y2=2.5 cos π=-2.5 m,由此可知,小环下落的高度为Δy=y1-y2=-1.25 m-(-2.5) m=1.25 m由动能定理得:mgΔy=
时,y2=2.5 cos π=-2.5 m,由此可知,小环下落的高度为Δy=y1-y2=-1.25 m-(-2.5) m=1.25 m由动能定理得:mgΔy= mv2-
mv2- mv02,代入数值得:v=
mv02,代入数值得:v= m/s.当小环速度为零时,设上升的高度为h,由动能定理得:-mgh=0-
m/s.当小环速度为零时,设上升的高度为h,由动能定理得:-mgh=0- mv02,则h=
mv02,则h=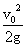 =1.25
m,故当y=0时,小环速度为零,所以有2.5cos (kx+
=1.25
m,故当y=0时,小环速度为零,所以有2.5cos (kx+ π)=0,得x=
π)=0,得x= π
π
7.(07天津理综15)如图所示,物体A静止在光滑的水平面上,A的左边固定有轻质弹簧,与A质量相等的物体B以速度v向A运动并与弹簧发生碰撞.A、B始终沿同一直线运动,则A、B组成的系统动能损失最大的时刻是 ( )
 A.A开始运动时
A.A开始运动时
B.A的速度等于v时
C.B的速度等于零时
D.A和B的速度相等时
答案 D
解析 A、B两物体碰撞过程中动量守恒,当A、B两物体速度相等时,系统动能损失最大,损失的动能转化成弹簧的弹性势能.
6.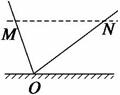 (07山东理综20)如图所示,光滑轨道MO和ON底端对接且ON=2MO,M、N两点高度相同.小球自M点由静止自由滚下,忽略小球经过O点时的机械能损失,以v、S、a、E0、分别表示小球的速度、位移、加速度和动能四个物理量的大小.下列图象中能正确反映小球自M点到N点运动过程的是 ( )
(07山东理综20)如图所示,光滑轨道MO和ON底端对接且ON=2MO,M、N两点高度相同.小球自M点由静止自由滚下,忽略小球经过O点时的机械能损失,以v、S、a、E0、分别表示小球的速度、位移、加速度和动能四个物理量的大小.下列图象中能正确反映小球自M点到N点运动过程的是 ( )

答案 A?
解析 从M到O,v1=a1t,从O到N,v2=v1-a2t=(a1-a2)t,v与t是一次函数关系,所以A正确;从M到O,s= a1t2,则s与t的图象是抛物线,所以B错;从M到O和从O到N,加速度是常数,所以C错;从M到O,Ek=
a1t2,则s与t的图象是抛物线,所以B错;从M到O和从O到N,加速度是常数,所以C错;从M到O,Ek= mv12=
mv12= ma12t2,所以D错.
ma12t2,所以D错.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com