
4. (2009南京市).一个带电粒子在磁场力的作用下做匀速圆周运动,要想确定带电粒子的电荷量与质量之比,则只需要知道( B )
A.运动速度v和磁感应强度B
B.磁感应强度B和运动周期T
 C.轨道半径R和运动速度v
C.轨道半径R和运动速度v
D.轨道半径R和磁感应强度B
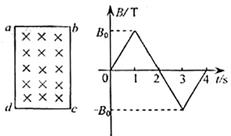
5(2009上海南汇区).矩形导线框abcd固定在匀强磁场中,磁感线的方向与导线框所在平面垂直。规定磁场的正方向垂直纸面向里,磁感应强度B随时间变化的规律如图所示.若规定顺时针方向为感应电流i的正方向,下列各图中正确的是 [ D ]

 6(2009山东威海一中3).如图所示,实线表示在竖直平面内的电场线,电场线与水平方向成α角,水平方向的匀强磁场与电场正交,有一带电液滴沿斜向上的虚线L做直线运动,L与水平方向成β角,且α>β,则下列说法中错误的是 ( D )
6(2009山东威海一中3).如图所示,实线表示在竖直平面内的电场线,电场线与水平方向成α角,水平方向的匀强磁场与电场正交,有一带电液滴沿斜向上的虚线L做直线运动,L与水平方向成β角,且α>β,则下列说法中错误的是 ( D )
A.液滴一定做匀速直线运动
B.液滴一定带正电
C.电场线方向一定斜向上
D.液滴有可能做匀变速直线运动
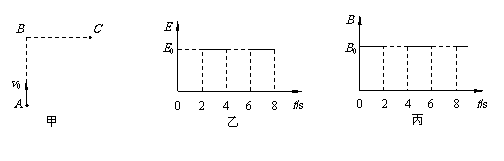
7(2009北京海淀区) 如图甲所示,在空间存在一个变化的电场和一个变化的磁场,电场的方向水平向右(图甲中由B到C),场强大小随时间变化情况如图乙所示;磁感应强度方向垂直于纸面、大小随时间变化情况如图丙所示。在t=1s时,从A点沿AB方向(垂直于BC)以初速度v0射出第一个粒子,并在此之后,每隔2s有一个相同的粒子沿AB方向均以初速度v0射出,并恰好均能击中C点,若AB=BC=l,且粒子由A运动到C的运动时间小于1s。不计空气阻力,对于各粒子由A运动到C的过程中,以下说法正确的是 ( BCD )
A.电场强度E0和磁感应强度B0的大小之比为3 v0:1
B.第一个粒子和第二个粒子运动的加速度大小之比为1:2
C.第一个粒子和第二个粒子运动的时间之比为π:2
D.第一个粒子和第二个粒子通过C的动能之比为 1:5
 8(2009年湖南郴州市高三调研试题).如图所示,带电金属小球用绝缘丝线系住,丝线上端固定,形成一个单摆.如果在摆球经过的区域加上如图所示的磁场,不计摩擦及
8(2009年湖南郴州市高三调研试题).如图所示,带电金属小球用绝缘丝线系住,丝线上端固定,形成一个单摆.如果在摆球经过的区域加上如图所示的磁场,不计摩擦及
空气阻力,下列说法中正确的是(AD)
A.单摆周期不变
B.单摆周期变大
C.单摆的振幅逐渐减小
D.摆球在最大位移处所受丝线的拉力大小不变
9(2009年安徽合肥35中高三物理第一次质量抽测试卷)某匀强磁场垂直穿过一个线圈平面,磁感强度B随时间t变化的规律如图线所示.若在某1s内穿过线圈中磁通量的变化量为零,则该1s 开始的时刻是 ( C )
A.第1.51s B.第1.69 s C.第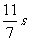 D.第
D.第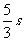
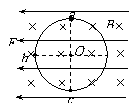
10(2009山东泰安一模) 如图甲所示为一个质量为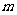 、电荷量为
、电荷量为 的圆环,可在水平放置的足够长的粗糙细杆上滑动,细杆处于磁感应强度为B的匀强磁场中,(不计空气阻力),现给圆环向右初速度
的圆环,可在水平放置的足够长的粗糙细杆上滑动,细杆处于磁感应强度为B的匀强磁场中,(不计空气阻力),现给圆环向右初速度 ,在以后的运动过程中,圆环运动的速度图象可能是图乙中的( AC )
,在以后的运动过程中,圆环运动的速度图象可能是图乙中的( AC )
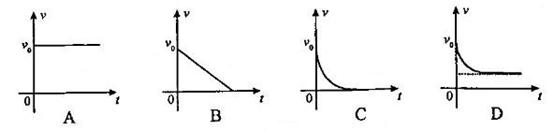
3. (2009北京西城区) 如图,空间存在水平向左的匀强电场和垂直纸面向里的匀强磁场,电场和磁场相互垂直。在电磁场区域中,有一个竖直放置的光滑绝缘圆环,环上套有一个带正电的小球。O点为圆环的圆心,a、b、c为圆环上的三个点,a点为最高点,c点为最低点,Ob沿水平方向。已知小球所受电场力与重力大小相等。现将小球从环的顶端a点由静止释放。下列判断正确的是( D )
(2009北京西城区) 如图,空间存在水平向左的匀强电场和垂直纸面向里的匀强磁场,电场和磁场相互垂直。在电磁场区域中,有一个竖直放置的光滑绝缘圆环,环上套有一个带正电的小球。O点为圆环的圆心,a、b、c为圆环上的三个点,a点为最高点,c点为最低点,Ob沿水平方向。已知小球所受电场力与重力大小相等。现将小球从环的顶端a点由静止释放。下列判断正确的是( D )
A.当小球运动的弧长为圆周长的1/4时,洛仑兹力最大
B.当小球运动的弧长为圆周长的1/2时,洛仑兹力最大
C.小球从a点到b点,重力势能减小,电势能增大
D.小球从b点运动到c点,电势能增大,动能先增大后减小
2.(2009湛江市)唱卡拉OK用的话筒,内有传感器,其中有一种是动圈式的,它的工作原理是在弹性膜片后面粘接一个轻小的金属线圈,线圈处于永磁体的磁场中,当声波使膜片前后振动时,就将声音信号转变为电信号,下列说法正确的是 ( BD )
A. 该传感器是根据电流的磁效应工作的
B. 该传感器是根据电磁感应原理工作的
C.膜片振动时,穿过金属线圈的磁通量总是增加的
D. 膜片振动时,金属线圈中产生感应电动势
1.(2009年山东省实验中学) 如图所示,在第二象限内有水平向右的匀强电场,电场强度为E,在第一、第四象限内分别存在如图所示的匀强磁场,磁感应强度大小相等. 有一个带电粒子以初速度v0垂直x轴,从x轴上的P点进入匀强电场,恰好与y轴成45°角射出电场,再经过一段时间又恰好垂直于x轴进入下面的磁场.已知OP之间的距离为d,则带电粒子 ( AD )
A.在电场中运动的时间为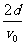
B.在磁场中做圆周运动的半径为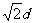
C.自进入磁场至第二次经过x轴所用时间为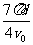
D.自进入电场至在磁场中第二次经过x轴的时间为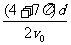
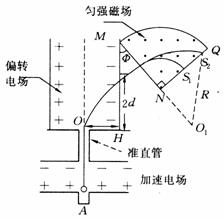
24.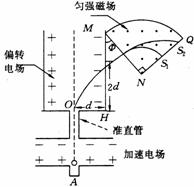 (09年重庆卷)25.(19分)如题25图,离子源A产生的初速为零、带电量均为e、质量不同的正离子被电压为U0的加速电场加速后匀速通过准直管,垂直射入匀强偏转电场,偏转后通过极板HM上的小孔S离开电场,经过一段匀速直线运动,垂直于边界MN进入磁感应强度为B的匀强磁场。已知HO=d,HS=2d,
(09年重庆卷)25.(19分)如题25图,离子源A产生的初速为零、带电量均为e、质量不同的正离子被电压为U0的加速电场加速后匀速通过准直管,垂直射入匀强偏转电场,偏转后通过极板HM上的小孔S离开电场,经过一段匀速直线运动,垂直于边界MN进入磁感应强度为B的匀强磁场。已知HO=d,HS=2d,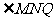 =90°。(忽略粒子所受重力)
=90°。(忽略粒子所受重力)
(1)求偏转电场场强E0的大小以及HM与MN的夹角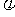 ;
;
(2)求质量为m的离子在磁场中做圆周运动的半径;
(3)若质量为4m的离子垂直打在NQ的中点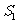 处,质量为16m的离子打在
处,质量为16m的离子打在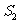 处。求
处。求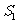 和
和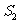 之间的距离以及能打在NQ上的正离子的质量范围。
之间的距离以及能打在NQ上的正离子的质量范围。
解析:

2009年联考题
23.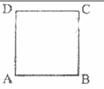 (09年海南物理)16.(10分)如图,ABCD是边长为
(09年海南物理)16.(10分)如图,ABCD是边长为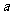 的正方形。质量为
的正方形。质量为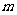 、电荷量为
、电荷量为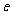 的电子以大小为
的电子以大小为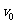 的初速度沿纸面垂直于BC变射入正方形区域。在正方形内适当区域中有匀强磁场。电子从BC边上的任意点入射,都只能从A点射出磁场。不计重力,求:
的初速度沿纸面垂直于BC变射入正方形区域。在正方形内适当区域中有匀强磁场。电子从BC边上的任意点入射,都只能从A点射出磁场。不计重力,求:
(1)次匀强磁场区域中磁感应强度的方向和大小;
(2)此匀强磁场区域的最小面积。
解析:(1)设匀强磁场的磁感应强度的大小为B。令圆弧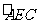 是自C点垂直于BC入射的电子在磁场中的运行
是自C点垂直于BC入射的电子在磁场中的运行
轨道。电子所受到的磁场的作用力
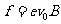
应指向圆弧的圆心,因而磁场的方向应垂直于纸面向外。圆弧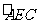 的圆心在CB边或其延长线上。依题意, 圆心在A、C连线的中垂线上,故B 点即为圆心,圆半径为
的圆心在CB边或其延长线上。依题意, 圆心在A、C连线的中垂线上,故B 点即为圆心,圆半径为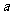 按照牛顿定律有
按照牛顿定律有
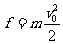
联立①②式得
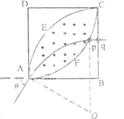
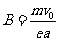
(2)由(1)中决定的磁感应强度的方向和大小,可知自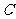 点垂直于
点垂直于 入射电子在A点沿DA方向射出,且自BC边上其它点垂直于入射的电子的运动轨道只能在BAEC区域中。因而,圆弧
入射电子在A点沿DA方向射出,且自BC边上其它点垂直于入射的电子的运动轨道只能在BAEC区域中。因而,圆弧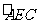 是所求的最小磁场区域的一个边界。
是所求的最小磁场区域的一个边界。
为了决定该磁场区域的另一边界,我们来考察射中A点的电子的速度方向与BA的延长线交角为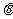 (不妨设
(不妨设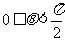 )的情形。该电子的运动轨迹
)的情形。该电子的运动轨迹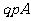 如图所示。
如图所示。
图中,圆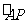 的圆心为O,pq垂直于BC边 ,由③式知,圆弧
的圆心为O,pq垂直于BC边 ,由③式知,圆弧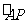 的半径仍为
的半径仍为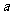 ,在D为原点、DC为x轴,AD为
,在D为原点、DC为x轴,AD为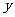 轴的坐标系中,P点的坐标
轴的坐标系中,P点的坐标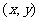 为
为
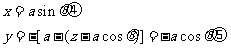
这意味着,在范围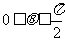 内,p点形成以D为圆心、
内,p点形成以D为圆心、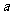 为半径的四分之一圆周
为半径的四分之一圆周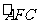 ,它是电子做直线运动和圆周运动的分界线,构成所求磁场区域的另一边界。
,它是电子做直线运动和圆周运动的分界线,构成所求磁场区域的另一边界。
因此,所求的最小匀强磁场区域时分别以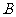 和
和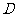 为圆心、
为圆心、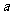 为半径的两个四分之一圆周
为半径的两个四分之一圆周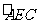 和
和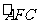 所围成的,其面积为
所围成的,其面积为
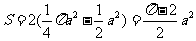
评分参考:本题10分。第(1)问4分,①至③式各1分;得出正确的磁场方向的,再给1分。第(2)问6分,得出“圆弧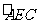 是所求磁场区域的一个边界”的,给2分;得出所求磁场区域的另一个边界的,再给2分;⑥式2分。
是所求磁场区域的一个边界”的,给2分;得出所求磁场区域的另一个边界的,再给2分;⑥式2分。
22.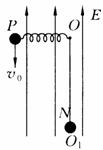 (09年四川卷)25.(20分)如图所示,轻弹簧一端连于固定点O,可在竖直平面内自由转动,另一端连接一带电小球P,其质量m=2×10-2
kg,电荷量q=0.2 C.将弹簧拉至水平后,以初速度V0=20 m/s竖直向下射出小球P,小球P到达O点的正下方O1点时速度恰好水平,其大小V=15 m/s.若O、O1相距R=1.5 m,小球P在O1点与另一由细绳悬挂的、不带电的、质量M=1.6×10-1 kg的静止绝缘小球N相碰。碰后瞬间,小球P脱离弹簧,小球N脱离细绳,同时在空间加上竖直向上的匀强电场E和垂直于纸面的磁感应强度B=1T的弱强磁场。此后,小球P在竖直平面内做半径r=0.5 m的圆周运动。小球P、N均可视为质点,小球P的电荷量保持不变,不计空气阻力,取g=10 m/s2。那么,
(09年四川卷)25.(20分)如图所示,轻弹簧一端连于固定点O,可在竖直平面内自由转动,另一端连接一带电小球P,其质量m=2×10-2
kg,电荷量q=0.2 C.将弹簧拉至水平后,以初速度V0=20 m/s竖直向下射出小球P,小球P到达O点的正下方O1点时速度恰好水平,其大小V=15 m/s.若O、O1相距R=1.5 m,小球P在O1点与另一由细绳悬挂的、不带电的、质量M=1.6×10-1 kg的静止绝缘小球N相碰。碰后瞬间,小球P脱离弹簧,小球N脱离细绳,同时在空间加上竖直向上的匀强电场E和垂直于纸面的磁感应强度B=1T的弱强磁场。此后,小球P在竖直平面内做半径r=0.5 m的圆周运动。小球P、N均可视为质点,小球P的电荷量保持不变,不计空气阻力,取g=10 m/s2。那么,
(1)弹簧从水平摆至竖直位置的过程中,其弹力做功为多少?
(2)请通过计算并比较相关物理量,判断小球P、N碰撞后能否在某一时刻具有相同的速度。
(3)若题中各量为变量,在保证小球P、N碰撞后某一时刻具有相同速度的前提下,请推导出
r的表达式(要求用B、q、m、θ表示,其中θ为小球N的运动速度与水平方向的夹角)。
解析:(1)设弹簧的弹力做功为W,有:

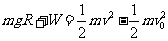 ①
①
代入数据,得:W=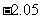 J②
J②
(2)由题给条件知,N碰后作平抛运动,P所受电场力和重力平衡,P带正电荷。设P、N碰后的速度大小
分别为v1和V,并令水平向右为正方向,有: 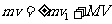 ③
③
而:  ④
④
若P、N碰后速度同向时,计算可得V<v1,这种碰撞不能实现。P、N碰后瞬时必为反向运动。
有: 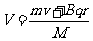 ⑤
⑤
P、N速度相同时,N经过的时间为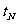 ,P经过的时间为
,P经过的时间为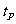 。设此时N的速度V1的方向与水平方向的夹角为
。设此时N的速度V1的方向与水平方向的夹角为
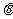 ,有:
,有:
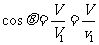 ⑥
⑥
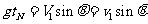 ⑦
⑦
代入数据,得: 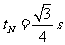 ⑧
⑧
对小球P,其圆周运动的周期为T,有:
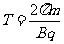 ⑨
⑨
经计算得: 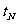 <T,
<T,
P经过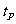 时,对应的圆心角为
时,对应的圆心角为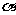 ,有:
,有:
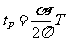 ⑩
⑩
当B的方向垂直纸面朝外时,P、N的速度相同,如图可知,有: 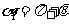
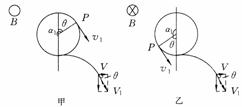
联立相关方程得: 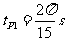
比较得, 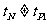 ,在此情况下,P、N的速度在同一时刻不可能相同。
,在此情况下,P、N的速度在同一时刻不可能相同。
当B的方向垂直纸面朝里时,P、N的速度相同,同样由图,有: 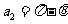 ,
,
同上得: 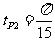 ,
,
比较得, 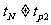 ,在此情况下,P、N的速度在同一时刻也不可能相同。
,在此情况下,P、N的速度在同一时刻也不可能相同。
(3)当B的方向垂直纸面朝外时,设在t时刻P、N的速度相同,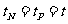 ,
,
再联立④⑦⑨⑩解得: 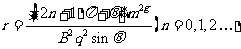
当B的方向垂直纸面朝里时,设在t时刻P、N的速度相同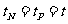 ,
,
同理得:  ,
,
考虑圆周运动的周期性,有: 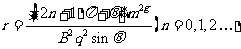
(给定的B、q、r、m、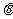 等物理量决定n的取值)
等物理量决定n的取值)
21.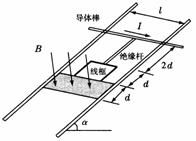 (09年江苏物理)15.(16分)如图所示,两平行的光滑金属导轨安装在一光滑绝缘斜面上,导轨间距为l、足够长且电阻忽略不计,导轨平面的倾角为
(09年江苏物理)15.(16分)如图所示,两平行的光滑金属导轨安装在一光滑绝缘斜面上,导轨间距为l、足够长且电阻忽略不计,导轨平面的倾角为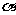 ,条形匀强磁场的宽度为d,磁感应强度大小为B、方向与导轨平面垂直。长度为2d的绝缘杆将导体棒和正方形的单匝线框连接在一起组成“
,条形匀强磁场的宽度为d,磁感应强度大小为B、方向与导轨平面垂直。长度为2d的绝缘杆将导体棒和正方形的单匝线框连接在一起组成“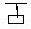 ”型装置,总质量为m,置于导轨上。导体棒中通以大小恒为I的电流(由外接恒流源产生,图中未图出)。线框的边长为d(d < l),电阻为R,下边与磁场区域上边界重合。将装置由静止释放,导体棒恰好运动到磁场区域下边界处返回,导体棒在整个运动过程中始终与导轨垂直。重力加速度为g。求:
”型装置,总质量为m,置于导轨上。导体棒中通以大小恒为I的电流(由外接恒流源产生,图中未图出)。线框的边长为d(d < l),电阻为R,下边与磁场区域上边界重合。将装置由静止释放,导体棒恰好运动到磁场区域下边界处返回,导体棒在整个运动过程中始终与导轨垂直。重力加速度为g。求:
(1)装置从释放到开始返回的过程中,线框中产生的焦耳热Q;
(2)线框第一次穿越磁场区域所需的时间t1;
(3)经过足够长时间后,线框上边与磁场区域下边界的最大距离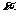 m。
m。
解析:(1)设装置由静止释放到导体棒运动到磁场下边界的过程中,作用在线框上的安培力做功为W
由动能定理 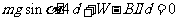
且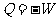
解得 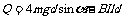
(2)设线框刚离开磁场下边界时的速度为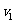 ,则接着向下运动
,则接着向下运动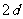
由动能定理 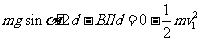
装置在磁场中运动时收到的合力
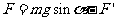

感应电动势  =Bd
=Bd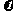
感应电流 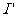 =
=
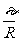
安培力 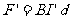
由牛顿第二定律,在t到t+ 时间内,有
时间内,有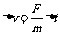
则
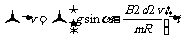
有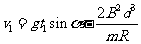
解得 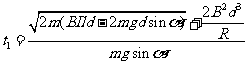
(3)经过足够长时间后,线框在磁场下边界与最大距离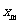 之间往复运动
之间往复运动
由动能定理 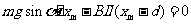
解得 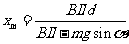
20.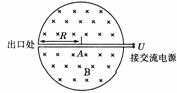 (09年江苏卷)14.(16分)1932年,劳伦斯和利文斯设计出了回旋加速器。回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计。磁感应强度为B的匀强磁场与盒面垂直。A处粒子源产生的粒子,质量为m、电荷量为+q ,在加速器中被加速,加速电压为U。加速过程中不考虑相对论效应和重力作用。
(09年江苏卷)14.(16分)1932年,劳伦斯和利文斯设计出了回旋加速器。回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计。磁感应强度为B的匀强磁场与盒面垂直。A处粒子源产生的粒子,质量为m、电荷量为+q ,在加速器中被加速,加速电压为U。加速过程中不考虑相对论效应和重力作用。
(1)求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比;
(2)求粒子从静止开始加速到出口处所需的时间t;
(3)实际使用中,磁感应强度和加速电场频率都有最大值的限制。若某一加速器磁感应强度和加速电场频率的最大值分别为Bm、fm,试讨论粒子能获得的最大动能E㎞。
解析:(1)设粒子第1次经过狭缝后的半径为r1,速度为v1
qu=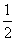 mv12
mv12
qv1B=m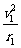
解得
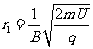
同理,粒子第2次经过狭缝后的半径 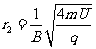
则 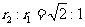
(2)设粒子到出口处被加速了n圈
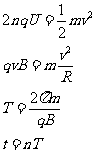
解得 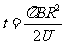
(3)加速电场的频率应等于粒子在磁场中做圆周运动的频率,即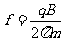
当磁场感应强度为Bm时,加速电场的频率应为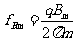
粒子的动能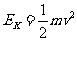
当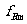 ≤
≤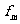 时,粒子的最大动能由Bm决定
时,粒子的最大动能由Bm决定
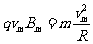
解得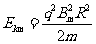
当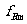 ≥
≥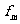 时,粒子的最大动能由fm决定
时,粒子的最大动能由fm决定
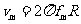
解得 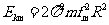
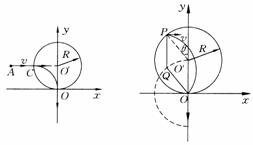
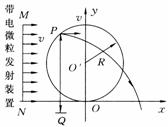
19.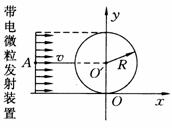 (09年浙江卷)25.(22分)如图所示,x轴正方向水平向右,y轴正方向竖直向上。在xOy平面内有与y轴平行的匀强电场,在半径为R的圆内还有与xOy平面垂直的匀强磁场。在圆的左边放置一带电微粒发射装置,它沿x轴正方向发射出一束具有相同质量m、电荷量q(q>0)和初速度v的带电微粒。发射时,这束带电微粒分布在0<y<2R的区间内。已知重力加速度大小为g。
(09年浙江卷)25.(22分)如图所示,x轴正方向水平向右,y轴正方向竖直向上。在xOy平面内有与y轴平行的匀强电场,在半径为R的圆内还有与xOy平面垂直的匀强磁场。在圆的左边放置一带电微粒发射装置,它沿x轴正方向发射出一束具有相同质量m、电荷量q(q>0)和初速度v的带电微粒。发射时,这束带电微粒分布在0<y<2R的区间内。已知重力加速度大小为g。
(1)从A点射出的带电微粒平行于x轴从C点进入有磁场区域,并从坐标原点O沿y轴负方向离开,求点场强度和磁感应强度的大小和方向。
(2)请指出这束带电微粒与x轴相交的区域,并说明理由。
(3)若这束带电微粒初速度变为2v,那么它们与x轴相交的区域又在哪里?并说明理由。
答案:(1)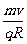 ;方向垂直于纸面向外;(2)见解析;(3)与x同相交的区域范围是x>0。
;方向垂直于纸面向外;(2)见解析;(3)与x同相交的区域范围是x>0。
解析:本题考查带电粒子在复合场中的运动。
带电粒子平行于x轴从C点进入磁场,说明带电微粒所受重力和电场力平衡。设电场强度大小为E,由
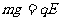
可得
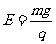
方向沿y轴正方向。
带电微粒进入磁场后,将做圆周运动。 且
r=R
如图(a)所示,设磁感应强度大小为B。由

得
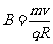
方向垂直于纸面向外
 (2)这束带电微粒都通过坐标原点。
(2)这束带电微粒都通过坐标原点。
方法一:从任一点P水平进入磁场的带电微粒在磁场中做半径为R的匀速圆周运动,其圆心位于其正下方的Q点,如图b所示,这束带电微粒进入磁场后的圆心轨迹是如图b的虚线半圆,此圆的圆心是坐标原点为。
方法二:从任一点P水平进入磁场的带电微粒在磁场中做半径为R的匀速圆周运动。如图b示,高P点与O′点的连线与y轴的夹角为θ,其圆心Q的坐标为(-Rsinθ,Rcosθ),圆周运动轨迹方程为
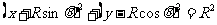
得
x=0 x=-Rsinθ
y=0 或 y=R(1+cosθ)
 (3)这束带电微粒与x轴相交的区域是x>0
(3)这束带电微粒与x轴相交的区域是x>0
带电微粒在磁场中经过一段半径为r′的圆弧运动后,将在y同的右方(x>0)的区域离开磁场并做匀速直线运动,如图c所示。靠近M点发射出来的带电微粒在突出磁场后会射向x同正方向的无穷远处国靠近N点发射出来的带电微粒会在靠近原点之处穿出磁场。所以,这束带电微粒与x同相交的区域范围是x>0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com