
7.关于函数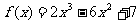 ,下列说法不正确的是
( )
,下列说法不正确的是
( )
A.在区间( ,0)内,
,0)内, 为增函数
为增函数
B.在区间(0,2)内, 为减函数
为减函数
C.在区间(2, )内,
)内, 为增函数
为增函数
D.在区间( ,0)
,0) 内,
内, 为增函数
为增函数
6.一直线运动的物体,从时间t到t+△t时,物体的位移为△s,那么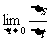 为( )
为( )
A.从时间t到t+△t时,物体的平均速度
B.时间t时该物体的瞬时速度
C.当时间为△t 时该物体的速度
D.从时间t到t+△t时位移的平均变化率
5.函数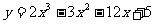 在[0,3]上的最大值、最小值分别是
( )
在[0,3]上的最大值、最小值分别是
( )
A.5,-15 B.5,-4 C.-4,-15 D.5,-16
4.若函数f(x)的导数为f′(x)=-sinx,则函数图像在点(4,f(4))处的切线的倾斜角为( )
A.90° B.0° C.锐角 D.钝角
3.曲线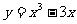 上切线平行于x轴的点的坐标是
( )
上切线平行于x轴的点的坐标是
( )
A.(-1,2) B.(1,-2) C.(1,2) D.(-1,2)或(1,-2)
2.若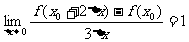 ,则
,则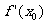 等于
( )
等于
( )
A.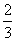 B.
B.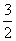 C.3
D.2
C.3
D.2
1.设函数f(x)在 处可导,则
处可导,则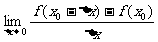 等于 ( )
等于 ( )
A.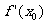 B.
B.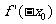 C.
C.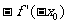 D.
D.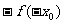
例1(08山东)设函数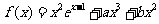 ,已知
,已知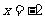 和
和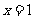 为
为 的极值点.
的极值点.
(Ⅰ)求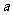 和
和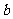 的值;
的值;
(Ⅱ)讨论 的单调性;
的单调性;
(Ⅲ)设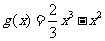 ,试比较
,试比较 与
与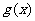 的大小.
的大小.
解:(Ⅰ)因为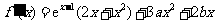
 ,
,
又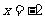 和
和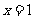 为
为 的极值点,所以
的极值点,所以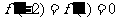 ,
,
因此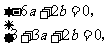
解方程组得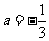 ,
,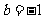 .
.
(Ⅱ)因为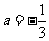 ,
,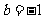 ,
,
所以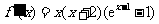 ,
,
令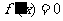 ,解得
,解得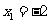 ,
,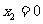 ,
,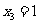 .
.
因为当
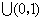 时,
时,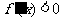 ;
;
当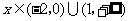 时,
时,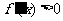 .
.
所以 在
在 和
和 上是单调递增的;
上是单调递增的;
在 和
和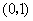 上是单调递减的.
上是单调递减的.
(Ⅲ)由(Ⅰ)可知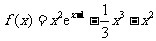 ,
,
故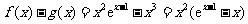 ,
,
令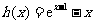 ,
,
则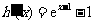 .
.
令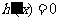 ,得
,得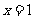 ,
,
因为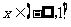 时,
时,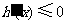 ,
,
所以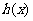 在
在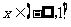 上单调递减.
上单调递减.
故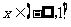 时,
时,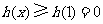 ;
;
因为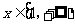 时,
时,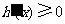 ,
,
所以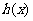 在
在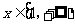 上单调递增.
上单调递增.
故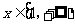 时,
时,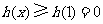 .
.
所以对任意 ,恒有
,恒有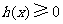 ,又
,又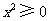 ,
,
因此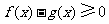 ,
,
故对任意 ,恒有
,恒有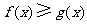 .
.
说明:本题主要考查函数的极值及利用导数解决函数单调性问题,另外利用导数证明不等式也是09年高考不科忽视的考查方向.
例2.(08北京)已知函数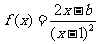 ,求导函数
,求导函数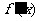 ,并确定
,并确定 的单调区间.
的单调区间.
解: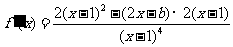
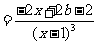
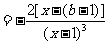 .
.
令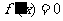 ,得
,得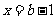 .
.
当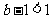 ,即
,即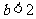 时,
时,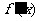 的变化情况如下表:
的变化情况如下表:
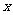 |
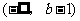 |
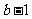 |
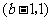 |
 |
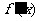 |
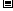 |
0 |
 |
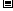 |
当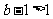 ,即
,即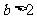 时,
时,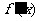 的变化情况如下表:
的变化情况如下表:
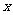 |
 |
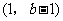 |
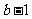 |
 |
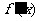 |
 |
 |
0 |
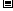 |
所以,当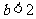 时,函数
时,函数 在
在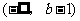 上单调递减,在
上单调递减,在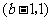 上单调递增,
上单调递增,
在 上单调递减.
上单调递减.
当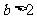 时,函数
时,函数 在
在 上单调递减,在
上单调递减,在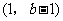 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
当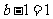 ,即
,即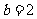 时,
时,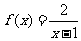 ,所以函数
,所以函数 在
在 上单调递减,在
上单调递减,在 上单调递减.
上单调递减.
例3.(08天津)已知函数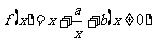 ,其中
,其中 .
.
(Ⅰ)若曲线 在点
在点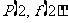 处的切线方程为
处的切线方程为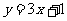 ,求函数
,求函数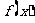 的解析式;
的解析式;
(Ⅱ)讨论函数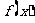 的单调性;
的单调性;
(Ⅲ)若对于任意的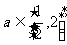 ,不等式
,不等式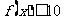 在
在 上恒成立,求
上恒成立,求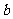 的取值范围.
的取值范围.
解:(Ⅰ)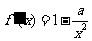 ,由导数的几何意义得
,由导数的几何意义得 ,于是
,于是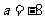 .
.
由切点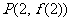 在直线
在直线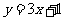 上可得
上可得 ,解得
,解得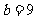 .
.
所以函数 的解析式为
的解析式为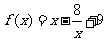 .
.
(Ⅱ)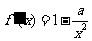 .
.
当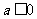 时,显然
时,显然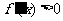 (
(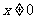 ).这时
).这时 在
在 ,
, 内是增函数.
内是增函数.
当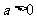 时,令
时,令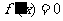 ,解得
,解得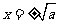 .
.
当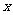 变化时,
变化时,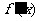 ,
, 的变化情况如下表:
的变化情况如下表:
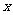 |
 |
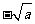 |
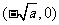 |
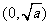 |
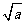 |
 |
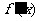 |
+ |
0 |
- |
- |
0 |
+ |
 |
↗ |
极大值 |
↘ |
↘ |
极小值 |
↗ |
所以 在
在 ,
, 内是增函数,在
内是增函数,在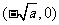 ,(0,
,(0,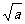 )内是减函数.
)内是减函数.
(Ⅲ)由(Ⅱ)知, 在
在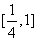 上的最大值为
上的最大值为 与
与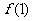 中的较大者,对于任意的
中的较大者,对于任意的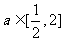 ,不等式
,不等式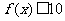 在
在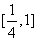 上恒成立,当且仅当
上恒成立,当且仅当 ,即
,即 ,对任意的
,对任意的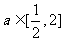 成立.
成立.
从而得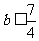 ,所以满足条件的
,所以满足条件的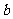 的取值范围是
的取值范围是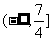 .
.
说明:本小题主要考查导数的几何意义、利用导数研究函数的单调性、解不等式等基础知识,考查运算能力、综合分析和解决问题的能力.
例4.(08湖北)水库的蓄水量随时间而变化,现用t表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为
V(t)=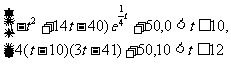
(Ⅰ)该水库的蓄水量小于50的时期称为枯水期.以i-1<t<i表示第i月份(i=1,2,…,12),问一年内哪几个月份是枯水期?
(Ⅱ)求一年内该水库的最大蓄水量(取e=2.7计算).
解:(Ⅰ)①当0<t 10时,V(t)=(-t2+14t-40)
10时,V(t)=(-t2+14t-40)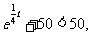
化简得t2-14t+40>0,
解得t<4,或t>10,又0<t 10,故0<t<4.
10,故0<t<4.
②当10<t 12时,V(t)=4(t-10)(3t-41)+50<50,
12时,V(t)=4(t-10)(3t-41)+50<50,
化简得(t-10)(3t-41)<0,
解得10<t<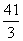 ,又10<t
,又10<t 12,故 10<t
12,故 10<t 12.
12.
综合得0<t<4,或10<t 12,
12,
故知枯水期为1月,2月, 3月,4月,11月,12月共6个月.
(Ⅱ)由(Ⅰ)知:V(t)的最大值只能在(4,10)内达到.
由V′(t)=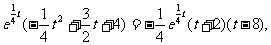

令V′(t)=0,解得t=8(t=-2舍去).
当t变化时,V′(t) 与V (t)的变化情况如下表:
|
t |
(4,8) |
8 |
(8,10) |
|
V′(t) |
+ |
0 |
- |
|
V(t) |
 |
极大值 |
 |
由上表,V(t)在t=8时取得最大值V(8)=8e2+50-108.32(亿立方米).
故知一年内该水库的最大蓄水量是108.32亿立方米
说明:本小题主要考查函数、导数和不等式等基本知识,考查用导数求最值和综合运用数学知识解决实际问题能力.
例5.(08陕西)已知函数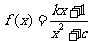 (
(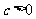 且
且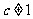 ,
,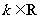 )恰有一个极大值点和一个极小值点,其中一个是
)恰有一个极大值点和一个极小值点,其中一个是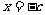 .
.
(Ⅰ)求函数 的另一个极值点;
的另一个极值点;
(Ⅱ)求函数 的极大值
的极大值 和极小值
和极小值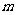 ,并求
,并求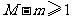 时
时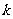 的取值范围.
的取值范围.
解:(Ⅰ)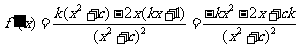 ,由题意知
,由题意知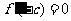 ,
,
即得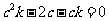 ,(*)
,(*)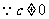 ,
,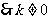 .
.
由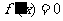 得
得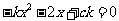 ,
,
由韦达定理知另一个极值点为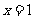 (或
(或 ).
).
(Ⅱ)由(*)式得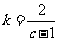 ,即
,即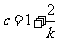 .
.
当 时,
时,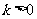 ;当
;当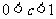 时,
时, .
.
(i)当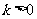 时,
时, 在
在 和
和 内是减函数,在
内是减函数,在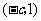 内是增函数.
内是增函数.
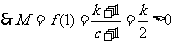 ,
,
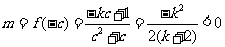 ,
,
由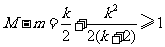 及
及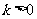 ,解得
,解得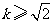 .
.
(ii)当 时,
时, 在
在 和
和 内是增函数,在
内是增函数,在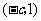 内是减函数.
内是减函数.
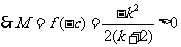 ,
,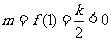
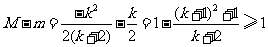 恒成立.
恒成立.
综上可知,所求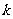 的取值范围为
的取值范围为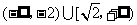 .
.
例6.求证下列不等式
(1)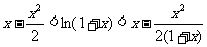

(2)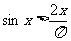
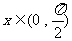
(3)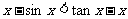
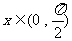
证明:(1)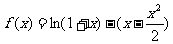
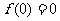
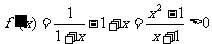
∴ 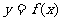 为
为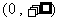 上
上 ∴
∴ 
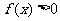 恒成立
恒成立
∴ 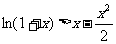
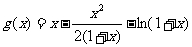
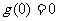
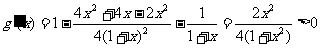
∴ 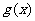 在
在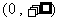 上
上 ∴
∴ 
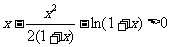 恒成立
恒成立
(2)原式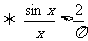 令
令 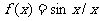
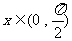
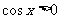
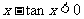
∴ 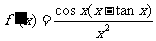 ∴
∴ 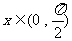
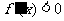
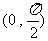
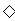
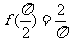 ∴
∴ 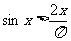
(3)令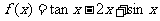
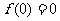
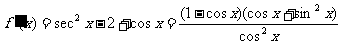
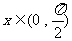
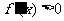 ∴
∴ 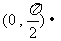
∴ 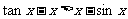
说明:利用导数证明不等式这一部分内容不可忽视,它本质是还是考查利用导数研究函数的单调性及最值问题。
8. 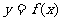

(1)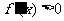 恒成立 ∴
恒成立 ∴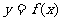 为
为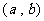 上
上
∴ 对任意 不等式
不等式 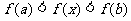 恒成立
恒成立
(2)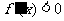 恒成立 ∴
恒成立 ∴ 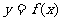 在
在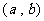 上
上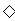
∴ 对任意 不等式
不等式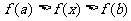 恒成立
恒成立
7. 导数与函数的单调性的关系
㈠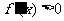 与
与 为增函数的关系。
为增函数的关系。
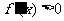 能推出
能推出 为增函数,但反之不一定。如函数
为增函数,但反之不一定。如函数 在
在 上单调递增,但
上单调递增,但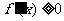 ,∴
,∴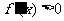 是
是 为增函数的充分不必要条件。
为增函数的充分不必要条件。
㈡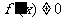 时,
时,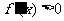 与
与 为增函数的关系。
为增函数的关系。
若将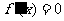 的根作为分界点,因为规定
的根作为分界点,因为规定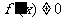 ,即抠去了分界点,此时
,即抠去了分界点,此时 为增函数,就一定有
为增函数,就一定有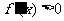 。∴当
。∴当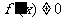 时,
时,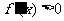 是
是 为增函数的充分必要条件。
为增函数的充分必要条件。
㈢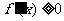 与
与 为增函数的关系。
为增函数的关系。
 为增函数,一定可以推出
为增函数,一定可以推出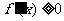 ,但反之不一定,因为
,但反之不一定,因为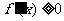 ,即为
,即为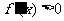 或
或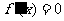 。当函数在某个区间内恒有
。当函数在某个区间内恒有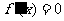 ,则
,则 为常数,函数不具有单调性。∴
为常数,函数不具有单调性。∴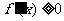 是
是 为增函数的必要不充分条件。
为增函数的必要不充分条件。
函数的单调性是函数一条重要性质,也是高中阶段研究的重点,我们一定要把握好以上三个关系,用导数判断好函数的单调性。因此新教材为解决单调区间的端点问题,都一律用开区间作为单调区间,避免讨论以上问题,也简化了问题。但在实际应用中还会遇到端点的讨论问题,要谨慎处理。
㈣单调区间的求解过程
已知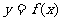
(1)分析 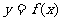 的定义域; (2)求导数
的定义域; (2)求导数 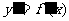
(3)解不等式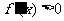 ,解集在定义域内的部分为增区间
,解集在定义域内的部分为增区间
(4)解不等式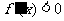 ,解集在定义域内的部分为减区间
,解集在定义域内的部分为减区间
我们在应用导数判断函数的单调性时一定要搞清以下三个关系,才能准确无误地判断函数的单调性。以下以增函数为例作简单的分析,前提条件都是函数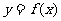 在某个区间内可导。
在某个区间内可导。
㈤函数单调区间的合并
函数单调区间的合并主要依据是函数 在
在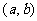 单调递增,在
单调递增,在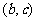 单调递增,又知函数在
单调递增,又知函数在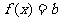 处连续,因此
处连续,因此 在
在 单调递增。同理减区间的合并也是如此,即相邻区间的单调性相同,且在公共点处函数连续,则二区间就可以合并为以个区间。
单调递增。同理减区间的合并也是如此,即相邻区间的单调性相同,且在公共点处函数连续,则二区间就可以合并为以个区间。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com