
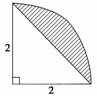
4.如图为一半径为2的扇形(其中扇形中心角为90°),在其内部随机地撒一粒黄豆,则它落在阴影部分的概率为 .
答案 1-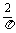
3.当你到一个红绿灯路口时,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为45秒,那么你看到黄灯的概率是 .
答案 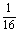
2.在长为10厘米的线段AB上任取一点G,用AG为半径作圆,则圆的面积介于36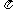 平方厘米到64
平方厘米到64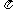 平方厘米的概率是
.
平方厘米的概率是
.
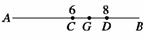
答案 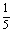
1.在区间(15,25]内的所有实数中随机取一个实数a,则这个实数满足17<a<20的概率是 .
答案 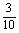
12.甲、乙两人进行投篮比赛,两人各投3球,谁投进的球数多谁获胜,已知每次投篮甲投进的概率为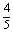 ,乙投进的概率为
,乙投进的概率为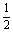 ,求:
,求:
(1)甲投进2球且乙投进1球的概率;
(2)在甲第一次投篮未投进的条件下,甲最终获胜的概率.
解 (1)甲投进2球的概率为
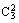
 ·
·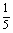 =
=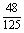 ,
,
乙投进1球的概率为
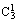
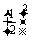 ·
·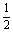 =
=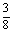 ,
,
甲投进2球且乙投进1球的概率为
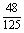 ×
×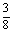 =
=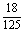 .
.
(2)在甲第一次投篮未进的条件下,甲获胜指甲后两投两进且乙三投一进或零进(记为A),或甲后两投一进且乙三投零进(记为B),
P(A)=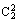
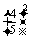 ·[
·[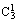
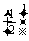 ·
·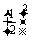 +
+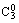
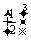 ]
]
= ×
×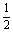 =
=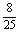 ,
,
P(B)=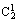
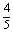 ·
·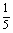 ·
·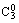
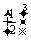
=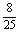 ×
×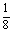 =
=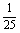 ,
,
故所求概率为P(A+B)= 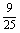 .
.
11.已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为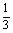 ,某植物研究所分两个小组分别独立开展该种子的发芽试验,每次试验种一粒种子,假定某次试验种子发芽,则称该次试验是成功的,如果种子没有发芽,则称该次试验是失败的.
,某植物研究所分两个小组分别独立开展该种子的发芽试验,每次试验种一粒种子,假定某次试验种子发芽,则称该次试验是成功的,如果种子没有发芽,则称该次试验是失败的.
(1)第一个小组做了三次试验,求至少两次试验成功的概率;
(2)第二个小组进行试验,到成功了4次为止,求在第四次成功之前共有三次失败,且恰有两次连续失败的概率.
解 (1)第一个小组做了三次试验,至少两次试验成功的概率是P(A)=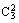
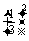 ·
·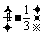 +
+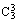
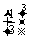 =
=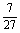 .
.
(2)第二个小组在第4次成功前,共进行了6次试验,其中三次成功三次失败,且恰有两次连续失败,其中各种可能的情况种数为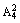 =12.因此所求的概率为
=12.因此所求的概率为
P(B)=12×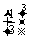
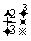 ·
·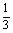 =
=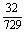 .
.
10.



 某计算机程序每运行一次都随机出现一个五位的二进制数A= a1 a2 a3 a4 a5 ,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为
某计算机程序每运行一次都随机出现一个五位的二进制数A= a1 a2 a3 a4 a5 ,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为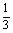 ,出现1的概率为
,出现1的概率为 .记
.记 =a1+a2+a3+a4+a5,当程序运行一次时,
=a1+a2+a3+a4+a5,当程序运行一次时,
(1)求 =3的概率;
=3的概率;
(2)求 的概率分布.
的概率分布.
解 (1)已知a1=1,要使 =3,只需后四位中出现2个1和2个0.
=3,只需后四位中出现2个1和2个0.
∴P( =3)=
=3)=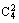
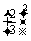 ·
·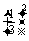 =
=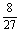 .
.
(2)  的可能取值为1,2,3,4,5.
的可能取值为1,2,3,4,5.
P( =1)=
=1)=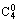
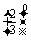 ·
·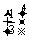 =
=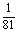 .
.
P( =2)=
=2)=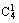
 ·
·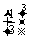 =
=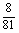 .
.
P( =3)=
=3)=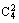
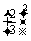 ·
·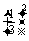 =
=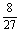 .
.
P( =4)=
=4)=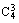
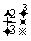 ·
·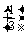 =
=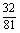 .
.
P( =5)=
=5)=
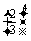 =
=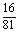 .
.
∴ 的概率分布为
的概率分布为
 |
1 |
2 |
3 |
4 |
5 |
|
P |
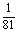 |
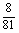 |
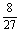 |
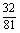 |
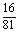 |
0.8,0.9.
(1)若甲和乙之间进行三场比赛,求甲恰好胜两场的概率;
(2)若四名运动员每两人之间进行一场比赛,求甲恰好胜两场的概率;
(3)若四名运动员每两人之间进行一场比赛,设甲获胜场次为 ,求随机变量
,求随机变量 的概率分布.
的概率分布.
解 (1)甲和乙之间进行三场比赛,甲恰好胜两场的概率为P=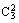 ×0.62×0.4=0.432.
×0.62×0.4=0.432.
(2)记“甲胜乙”,“甲胜丙”,“甲胜丁”三个事件分别为A,B,C,则P(A)=0.6,P(B)=0.8,P(C)=0.9.
则四名运动员每两人之间进行一场比赛,甲恰好胜两场的概率为
P(AB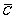 +A
+A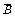 C+
C+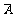 BC)
BC)
=P(A)P(B)[1-P(C)]+P(A)[1-P(B)]P(C)+[1-P(A)]P(B)P(C)
=0.6×0.8×0.1+0.6×0.2×0.9+0.4×0.8×0.9
=0.444.
(3)随机变量 的可能取值为0,1,2,3.
的可能取值为0,1,2,3.  的
的
P( =0)=0.4×0.2×0.1=0.008;
=0)=0.4×0.2×0.1=0.008;
P( =1)=0.6×0.2×0.1+0.4×0.8×0.1+0.4×0.2×0.9=0.116;
=1)=0.6×0.2×0.1+0.4×0.8×0.1+0.4×0.2×0.9=0.116;
由(2)得P( =2)=0.444;
=2)=0.444;
P( =3)=0.6×0.8×0.9=0.432.
=3)=0.6×0.8×0.9=0.432.
∴随机变量 的概率分布为
的概率分布为
 |
0 |
1 |
2 |
3 |
|
P |
0.008 |
0.116 |
0.444 |
0.432 |
9.有甲、乙、丙、丁四名网球运动员,通过对过去战绩的统计,在一场比赛中,甲对乙、丙、丁取胜的概率分别为0.6,
8.某射手射击1次,击中目标的概率是0.9.他连续射击4次,且各次射击是否击中目标相互之间没有影响.有下列结论:
①他第3次击中目标的概率是0.9;
②他恰好击中目标3次的概率是0.93×0.1;
③他至少击中目标1次的概率是1-0.14.
其中正确结论的序号是 (写出所有正确的结论的序号).
答案 ①③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com