
2、记录数据的方式示例
|
示例一-―数据关系 |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
W/×WJ |
1 |
2 |
3 |
4 |
5 |
6 |
|
X/×10-2m |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
|
v/v |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
|
示例二――倍数关系 |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
W/×WJ |
1 |
2 |
3 |
4 |
5 |
6 |
|
X/×10-2m |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
|
v/v |
v |
(X2 /X1)v |
(X3/X1)v |
(X4/X1)v |
(X5/X1)v |
(X6/X1)v |
1、采集橡皮条分别为一根、两根……、六根时的数据(匀速运动阶段,例如在0.1s内的位移),记在自己设计的表格中。
2、教师适时提出问题,指导学生操作的技巧,针对问题,完善实验操作。
(1)小车运动中会受到阻力,可以采用什么方法进行补偿?
可以采用平衡摩擦力的方法。具体操作是:使木板略微倾斜,将小车(车后拴纸带)放到木板上,轻推小车,小车运动,观察纸带的点距。调节木板的倾角,观察纸带的点距,直到点距相等,表明恰平衡摩擦力(若用气垫导轨,调节导轨的倾角,若挡光条遮光的时间通过数字毫秒计显示时间相等,即恰平衡摩擦力)。
(2)观察打点的纸带,点距是如何变化的?点距是否均匀?问题出在哪里?若恰能平衡摩擦力,试分析小车会做何种运动?应该采用哪些点距来计算小车的速度?
先增大,后减小。不均匀(不是匀加速)。没有平衡摩擦力。就要用到补偿法。先加速(但非匀加),后匀速。应采用小车做匀速运动那一段的点距来计算速度。因为匀速的速度就是橡皮条对小车作用的最终速度;由于小车在橡皮条变力作用下做非匀加速运动,最终速度不能用匀变速运动纸带的处理方法得到,但可以用匀速运动纸带的处理方法得到。
(3)使木板略微倾斜,调节木板的倾角,经检验恰好平衡摩擦力。可以做一系列地平行线,选适当的位置作为A,重新标出小车运动的初始位置A。(体现完善实验的过程)
(4)确立可操作实验方案,设计合理的实验步骤:
A.先将木板置于水平桌面,然后在钉有钢钉的长木板上,放好实验小车。
B.把打点计时器固定在木板的一端,将纸带穿过打点计时器的限位孔,纸带一端夹紧在小车的后端,打点计时器接电源。
C.使木板略微倾斜,调节木板的倾角,测量纸带点距直到相等,表明恰好平衡摩擦力。
D.过两钉中垂线上的适当位置作两钉的平行线,交中垂线于A点,作为小车每次运动的起始点。
E.使用一根橡皮筋时,将小车的前(或后)端拉到A点,接通电源,打点计时器打点,释放小车,小车离开木板前适时使小车制动,断开电源,取下纸带。重复本项前面的过程,选出清晰的纸带。记下点距相等后t=0.1s的位移 m,求出小车获得的速度v=10
m,求出小车获得的速度v=10 m/s。
m/s。
F.换用同样材料、粗细、长度的两根、三根、…六根橡皮筋,依照D项的方法,分别进行实验。记下各次实验中点距相等后t=0.1s的位移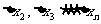 m,求出小车分别获得的速度
m,求出小车分别获得的速度 m/s。
m/s。
G.以功为纵轴(用第一次橡皮筋做的功为纵轴的单位长度),以速度为横轴(可以用适当的速度值为单位长度,也可以用第一次小车的速度为横轴的单位长度),建立坐标系,用描点法作出图像,看看是否是正比例图像,若不是,功与速度的哪种相关量(的变化量)是正比的,功就与速度的这种相关量(的变化量)具有确定的函数关系。
处理数据,得出规律
1、学生按确定方案开始初步实验。(首先完成实验操作方案的前四步)
2、确立基本的实验方案,设计初步的实验步骤:
A.先将木板置于水平桌面,然后在钉有钢钉的长木板上,放好实验小车。
B.把打点计时器固定在木板的一端,将纸带穿过打点计时器的限位孔,纸带一端夹紧在小车的后端,打点计时器接电源。
C.过两钉中垂线上的适当位置作两钉的平行线,交中垂线于O点,作为小车每次运动的起始点。
D.使用一根橡皮筋时,将小车的前端拉到O点,接通电源,打点计时器打点,释放小车,小车离开木板前适时使小车制动,断开电源,取下纸带。重复本项前面的过程,选出点迹清晰的纸带。(求出小车获得的速度。暂不求)
E.换用同样材料、粗细、长度的两根、三根、…六根橡皮筋,依照D项的方法,分别进行实验。(得出各次实验中小车分别获得的速度。暂不求)
F.以功为纵轴(第一次橡皮筋做的功为纵轴的单位长度),以速度为横轴(第一次小车的速度为横轴的单位长度),建立坐标系,用描点法作出图像,看看是否是正比例图像,若不是,功与速度的哪种相关量(的变化量)是正比的,功就与速度的这种相关量(的变化量)具有确定的函数关系。
学生实验,教师指导
1、制定基本的实验方案:(师生互动)互动以下面几个问题为中心展开:
(1)探究中,我们是否需要橡皮筋做功的具体数值?不需要。因为实验是以倍增的思想方法设计,若橡皮筋第一次做功为W,则橡皮筋第二次做功为2W,…、橡皮筋第n次做功为nW。且实验巧妙地将倍增的物理方法应用于变力做功。
(2)为了达到各次实验中橡皮筋做的功成倍增加,即实现倍增,对各次实验中橡皮筋的伸长量有什么要求?你想出了什么办法?各次实验中橡皮筋的伸长量必须相同。若使小车在橡皮筋的变力作用下产生的位移相同,就要有相同的运动起点。具体方法是:以第一次实验时小车前(或后)端的位置为基准,垂直运动方向在木板上作出一条水平线。以后改变橡皮筋的条数时,小车前(或后)端仍以此位置为基准(均从静止)运动。
(3)小车获得的速度怎样计算?小车在橡皮筋作用结束后,做匀速运动。找出纸带中点距相等的一段。求出点距相等一段的平均速度,即为小车匀速运动的速度,即小车加速后获得的速度。
(4)是否一定需要测出每次加速后小车速度的数值?可以怎样做?不一定需要。(当然,也可以测出每次加速后小车速度的数值)
设第一次小车获得的速度为v,小车在第一次、第二次、…、第n次实验中的速度为:  若令
若令 则
则 即小车在第二次以后实验中获得的速度可以用第一次实验中获得的速度的倍数来表示。
即小车在第二次以后实验中获得的速度可以用第一次实验中获得的速度的倍数来表示。
(5)实验完毕后,用什么方法分析橡皮筋对小车做的功与小车速度的关系?
图像法。
(6)如何在坐标纸上建立两轴物理量?如何确定适当的标度?
纵坐标表示橡皮筋对小车做的功,横坐标表示小车获得的速度。
以第一次实验时的功W为纵轴的单位长度(必须用),可以用第一次实验时的速度v为横轴的单位长度(也可以根据各次实验中的最大速度值、坐标纸的最大格数来确定),作出W-v曲线,即功-速度曲线。
2、过程与方法:通过用纸带与打点计时器来探究功与物体速度相关量变化的关系,体验知识的探究过程和物理学的研究方法。
1、知识与技能
(1)会用打点计时器打下的纸带计算物体运动的速度;
(2)学习利用物理图像探究功与物体速度变化的关系。
5.6 探究功与物体速度变化的关系
教学思路设计
前面几节课研究了重力做功与重力势能的关系,从而确立了重力势能的表达式。探究了弹力做功与弹性势能的关系,从而确立了弹性势能的表达式。这一节和下一节我们来探究功与物体动能的关系。
我们已经知道物体的动能与物体的速度有关,但我们还不能一下子就探究到功和物体动能的关系,我们先来探究力对物体做的功与物体速度变化的关系。
特别应该明确的是:本节课题《探究功与物体速度变化的关系》中物体速度变化不是指速度的变化量,而是指速度相关量的变化量。具体讲,可能是速度一次方的变化量,也可能是速度二次方的变化量、速度三次方的变化量…,还可能是速度二分之一次方的变化量…。所以我们探究的方向是功与物体速度相关量变化的关系,这样,我们探究起来才不会误入歧途。既不会只探究功与物体速度变化的关系,偏离探究方向;又不会狭隘的直接探究功与物体速度二次方变化的关系,功与物体速度三次方、二分之一次方变化的关系也要探究。要看看功与物体速度相关量变化到底是什么关系。
三维教学目标
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com