

16.(2009宁夏海南卷理)等差数列{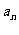 }前n项和为
}前n项和为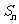 。已知
。已知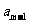 +
+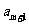 -
-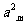 =0,
=0,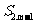 =38,则m=_______
=38,则m=_______
解析:由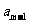 +
+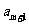 -
-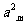 =0得到
=0得到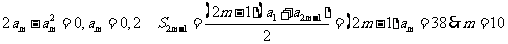 。
。
答案10
15.(2009辽宁卷理)等差数列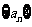 的前
的前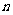 项和为
项和为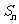 ,且
,且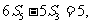 则
则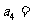
[解析]∵Sn=na1+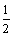 n(n-1)d .
n(n-1)d . 

∴S5=5a1+10d,S3=3a1+3d
∴6S5-5S3=30a1+60d-(15a1+15d)=15a1+45d=15(a1+3d)=15a4
[答案]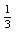
14.(2009山东卷文)在等差数列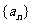 中,
中,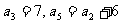 ,则
,则 .
.
[解析]:设等差数列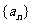 的公差为
的公差为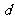 ,则由已知得
,则由已知得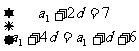 解得
解得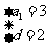 ,所以
,所以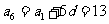 .
. 

答案:13.
[命题立意]:本题考查等差数列的通项公式以及基本计算.
13.(2009江苏卷)设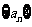 是公比为
是公比为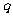 的等比数列,
的等比数列,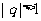 ,令
,令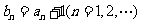 ,若数列
,若数列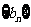 有连续四项在集合
有连续四项在集合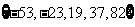 中,则
中,则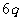 = .
= .
[解析] 考查等价转化能力和分析问题的能力。等比数列的通项。

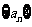 有连续四项在集合
有连续四项在集合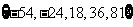 ,四项
,四项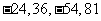 成等比数列,公比为
成等比数列,公比为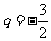 ,
,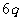 = -9
= -9
12.(2009浙江文)设等差数列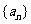 的前
的前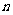 项和为
项和为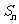 ,则
,则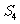 ,
, ,
,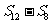 ,
,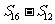 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列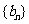 的前
的前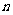 项积为
项积为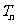 ,则
,则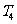 , , ,
, , ,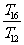 成等比数列.
成等比数列.
答案: 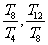 [命题意图]此题是一个数列与类比推理结合的问题,既考查了数列中等差数列和等比数列的知识,也考查了通过已知条件进行类比推理的方法和能力.
[命题意图]此题是一个数列与类比推理结合的问题,既考查了数列中等差数列和等比数列的知识,也考查了通过已知条件进行类比推理的方法和能力. 

[解析]对于等比数列,通过类比,有等比数列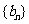 的前
的前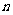 项积为
项积为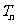 ,则
,则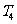 ,
,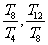 ,
,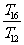 成等比数列.
成等比数列.
11.(2009浙江文)设等比数列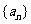 的公比
的公比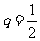 ,前
,前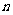 项和为
项和为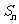 ,则
,则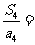 .
.
[命题意图]此题主要考查了数列中的等比数列的通项和求和公式,通过对数列知识点的考查充分体现了通项公式和前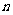 项和的知识联系.
项和的知识联系.
[解析]对于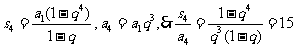 .
. 

10.(2009浙江理)设等比数列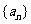 的公比
的公比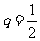 ,前
,前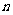 项和为
项和为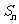 ,则
,则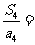 .
.
答案:15
[解析]对于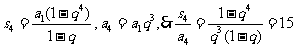
9.(2009安徽卷理)已知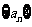 为等差数列,
为等差数列,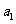 +
+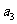 +
+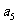 =105,
=105,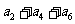 =99,以
=99,以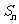 表示
表示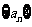 的前
的前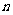 项和,则使得
项和,则使得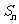 达到最大值的
达到最大值的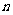 是
是
(A)21 (B)20 (C)19 (D) 18
[解析]:由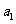 +
+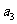 +
+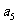 =105得
=105得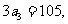 即
即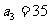 ,由
,由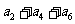 =99得
=99得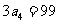 即
即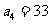 ,∴
,∴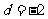 ,
,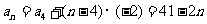 ,由
,由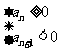 得
得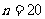 ,选B
,选B
8.(2009宁夏海南卷文)等差数列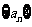 的前n项和为
的前n项和为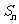 ,已知
,已知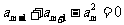 ,
,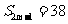 ,则
,则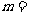
(A)38 (B)20
(C)10 (D)9 .


[答案]C
[解析]因为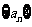 是等差数列,所以,
是等差数列,所以,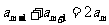 ,由
,由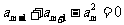 ,得:2
,得:2 -
-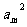 =0,所以,
=0,所以, =2,又
=2,又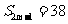 ,即
,即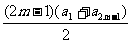 =38,即(2m-1)×2=38,解得m=10,故选.C。
=38,即(2m-1)×2=38,解得m=10,故选.C。
7.(2009宁夏海南卷理)等比数列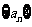 的前n项和为
的前n项和为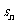 ,且4
,且4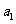 ,2
,2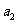 ,
,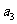 成等差数列。若
成等差数列。若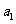 =1,则
=1,则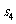 =
=
(A)7 (B)8 (3)15 (4)16
解析: 4
4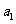 ,2
,2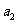 ,
,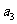 成等差数列,
成等差数列,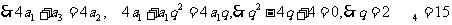 ,选C.
,选C.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com