
8、扩大3 倍 缩小3 倍 扩大3 倍 缩小3 倍
8、一个圆柱与一个圆锥等底等高,如果高要使它们的体积相等,则圆锥的高要 ,或者把圆柱的高 ;也可以把圆锥的底面积 ,或者把圆柱的底面积 。
B C C 4、 1:4 5、3.6 6、90 60 7、27
7、一个圆柱与一个圆锥的体积和底面积都都相等,圆柱的高是 9 分米,圆锥的高高高是 ( 27 )分米。
6、一个圆锥和一个圆柱等底等高,它们的的体积之和是 120 立方分米,这个圆圆柱的体积是( 90 )立方分米;圆锥体体积比圆柱少( 60 )立方分米。
5、把一个圆柱切削成一个最大的圆锥,已已知削去部分的体积比圆锥体积大3.6立方分米,那么圆锥的体积是 立方分米。
4、已知两个体积不同的圆柱,高相等,它们的底面半径的比是1∶2,那么它们的体积的比是
3、一个圆锥的体积是a立方米,则和它等底等高的圆柱体的体积是( )立方米。
A. 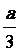 B. 2a C. 3a D.
B. 2a C. 3a D. 
2、甲乙两人分别利用一张长20厘米,宽15厘米的纸,用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱( )。
A.体积相等 B.用20厘米作为高的体积大
C. 用15厘米作为高的体积大 D. 无法比较
1、甲乙两人分别利用一张长20厘米,宽15厘米的纸,用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱( )。
A.高一定相等 B.侧面积一定相等
C. 侧面积和高都相等 D. 侧面积和高都不相等
例1:圆锥底面半径为10,母线长为60,底面圆周上一点B沿侧面绕两周回到B点那么最短距离为
例2:已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱.
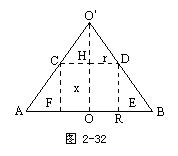
(1)求圆柱的侧面积;
(2)x为何值时,圆柱的侧面积最大?
分析:(1)首先要画出圆锥的轴截面△OAB,那么内接圆柱的轴截面为矩形CDEF,因为内接圆柱的高知道为x,故关键求r,怎样求r?(生:


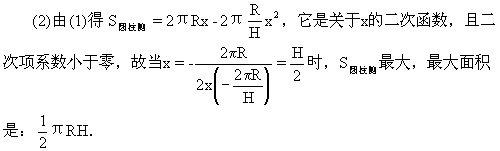
例3:如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足. (1)求证:AF⊥DB; (2)如果圆柱与三棱锥D-ABE的体积的比等于3π,求直线DE与平面ABCD所成的角.

解析 本题中,圆柱是“外包装”,三棱锥D-ABE是“骨架”,核心问题是平面和平面、直线和平面、直线和直线的位置关系.解答过程中多次考查各种垂直关系的性质和判定,还有角的计算.
证明(1)DA⊥平面ABE,∴DA⊥BE,又AE⊥BE,∴BE⊥平面ADE,
∴DE是直线DB在平面ADE内的射影,由AF⊥DE及三垂线定理,知AF⊥DB.
(2)过E作EH⊥AB,H是垂足,连结OH,由平面ABCD⊥平面ABE,知EH⊥平面ABCD,则∠EDH为直线DE与平面ABCD所成的角.
设圆柱底面半径为R,则DA=AB=2R,于是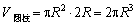 ,
,
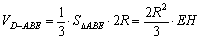 依题意:
依题意: ,得EH=R,
可知H是圆柱底面的圆心,∴AH=R,则
,得EH=R,
可知H是圆柱底面的圆心,∴AH=R,则 ,
∴
,
∴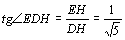 ,故所求角为
,故所求角为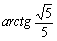 .
.
例4: 设圆锥底面圆周上两点A,B间的距离为2,圆锥顶点到直线AB的距离为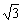 ,AB和圆锥的轴的距离为1,则该圆锥的体积为___________.
,AB和圆锥的轴的距离为1,则该圆锥的体积为___________.
解析 本题考查直线与直线的位置关系及圆锥体积公式的应用.

如图,依题意,有AB=2,SO⊥底面圆O,SC⊥AB于C,则SC=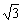 ,∴OC⊥AB,则OC=1 ∴SO=
,∴OC⊥AB,则OC=1 ∴SO= ,OA=
,OA= ∴
∴
例5. 已知圆锥底面直径AB=2,轴截面∠APB=90°,底面半径OC⊥AB
(1)求二面角B-PA-C的正切值
(2)求圆锥内接圆柱的最大侧面积及相应的高
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com