
(17)(本小题满分12分) ‘
已知 为锐角,且
为锐角,且 .
.
(1)求 的值;(2)求
的值;(2)求 的值
的值
(18)(本小题满分12分)
已知向量 .
.
(1)当 的值。
的值。
(2)求 的最小正周期和单调递增区间。
的最小正周期和单调递增区间。
(19)(本小题满分12分)
已知函数 (
( )的最小正周期为
)的最小正周期为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 在区间
在区间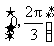 上的取值范围.
上的取值范围.
(20)(本小题满分12分)
已知函数 且
且 .
.
(1)求函数 定义域;判断函数
定义域;判断函数 的奇偶性,并予以证明;
的奇偶性,并予以证明;
(2)求使 的
的 的取值范围.
的取值范围.
(21)(本小题满分12分)
已知函数 (
( ,
, )为偶函数,且函数
)为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)将函数 的图象向右平移
的图象向右平移 个单位后,得到函数
个单位后,得到函数 的图象,求
的图象,求 的单调递减区间.
的单调递减区间.
(22)(本小题满分14分)
已知函数 =
= .
.
(1)用定义证明函数 在(-∞,+∞)上为减函数;
在(-∞,+∞)上为减函数;
(2)若x [1,2],求函数
[1,2],求函数 的值域;
的值域;
(3)若 =
= ,且当x
,且当x [1,2]时
[1,2]时
 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(13) 已知函数
(14) x为实数,f(x)为sinx与cosx中的较大者,设a≤f(x)≤b,则a+b=
(15) 函数 的图象恒过定点
的图象恒过定点 ,若点
,若点 在角
在角 的终边上,(o是坐标原点),则
的终边上,(o是坐标原点),则 =
=
(16) 不共线的向量 ,
, 的模都为2,若
的模都为2,若 ,
, ,则两向量
,则两向量 与
与 的夹角为
的夹角为
只有一项是符合题目要求的.
(1) 设集合 ,集合
,集合 ,
, ,则
,则 等于
等于
A.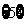 B.
B. C.
C.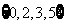 D.
D.
(2) 在三角形 中,
中,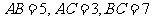 ,则
,则 的大小为( )
的大小为( )
A. B.
B. C.
C. D.
D.
(3)第二象限角 的正弦值为
的正弦值为 ,则正切值为
,则正切值为
A  B
B  C
C  D
D 
(4) 已知函数 则
则 是
( )
是
( )
A.最小正周期为 的奇函数 B.最小正周期为
的奇函数 B.最小正周期为 的偶函数
的偶函数
C.最小正周期为 的奇函数 D.最小正周期为
的奇函数 D.最小正周期为 的偶函数
的偶函数
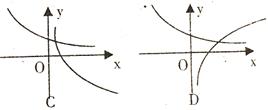
(5) 已知 ,
, ,若
,若 ,那么
,那么 与
与 在同一坐标系内的图像可能是
在同一坐标系内的图像可能是

(6)已知函数, ,则复合函数
,则复合函数
(A)  (B)
(B)  (C)
(C)
 (D)
(D) 
(7) 函数f(x)=x3+sinx+1(x∈R),若f(a)=2, 则f(-a)的值为( )
A.3 B.0 C.-1 D.-2
(8) 已知平面向量 ,
, ,
, 与
与 垂直,
垂直,
则 ( )
( )
A. B.
B. C.
C. D.
D.
(9)已知函数 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 则
则 的解析式是
的解析式是
(A)f(x)=x(x-2) (B)f(x)=|x|(x-2)
(C)f(x)= |x|(|x|-2) (D)f(x)=x(|x|-2)
(10)函数的图像如图所示,其中不能用二分法求函数零点的近似值的是( )
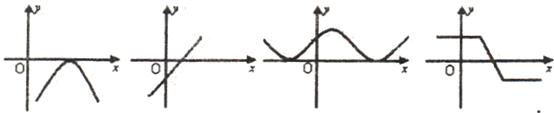
① ② ③ ④
(A)①② (B)①③ (C)①④ (D)③④
(11)若函数 在区间[2,+
在区间[2,+ )上是增函数,则a的取值范围( )
)上是增函数,则a的取值范围( )
(A)(- ,-3) (B)[3,+
,-3) (B)[3,+ ) (C)(-
) (C)(- ,3] (D)[-3,+
,3] (D)[-3,+ )
)
(12)某产品按质量分为10个档次,生产第一档(即最低档次)的利润是每件8元.每提高一个档次,利润每件增加2元,但每提高一个档次,在相同的时间内,产量减少3件,如果在规定的时间内,最低档次的产品可生产60件,则在同样的时间内,生产哪一档次的产品的总利润最大?( )
(A) 10 (B) 9 (C) 8 (D) 7
山东省北镇中学普通高中模块1、4寒假自测题
高一数学
第Ⅱ卷 (非选择题 共90分)
20.(14分)利用幂函数图象,画出下列函数的图象(写清步骤).
(1) .
.
19.(14分)由于对某种商品开始收税,使其定价比原定价上涨x成(即上涨率为 ),涨价后,商品卖出个数减少bx成,税率是新定价的a成,这里a,b均为正常数,且a<10,设售货款扣除税款后,剩余y元,要使y最大,求x的值.
),涨价后,商品卖出个数减少bx成,税率是新定价的a成,这里a,b均为正常数,且a<10,设售货款扣除税款后,剩余y元,要使y最大,求x的值.
18.(12分)下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系.


(A) (B) (C) (D) (E) (F)
17.(12分)求证:函数 在R上为奇函数且为增函数.
在R上为奇函数且为增函数.
16.(12分)已知幂函数 轴对称,试确定
轴对称,试确定 的解析式.
的解析式.
15.(12分)比较下列各组中两个值大小
(1)
14.幂函数 图象在一、二象限,不过原点,则
图象在一、二象限,不过原点,则 的奇偶性为
.
的奇偶性为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com