
12.以下四个命题:
①
②
③凸n边形内角和为 ④凸n边形对角线的条数是
④凸n边形对角线的条数是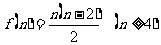
其中满足“假设 时命题成立,则当n=k+1时命题也成立’’.但不满足“当
时命题成立,则当n=k+1时命题也成立’’.但不满足“当 (
( 是题中给定的n的初始值)时命题成立”的命题序号是 .
是题中给定的n的初始值)时命题成立”的命题序号是 .
讲解 ①当n=3时, ,不等式成立;
,不等式成立;
② 当n=1时, ,但假设n=k时等式成立,则
,但假设n=k时等式成立,则
 ;
;
③ 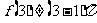 ,但假设
,但假设 成立,则
成立,则

④  ,假设
,假设 成立,则
成立,则

故应填②③.
11.列 中,
中,
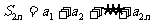 , 则
, 则

讲解 分类求和,得


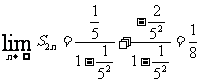 ,故应填
,故应填 .
.
10. 已知 是公差不为零的等差数列,如果
是公差不为零的等差数列,如果 是
是 的前n项和,那么
的前n项和,那么

讲解 特别取 ,有
,有 ,于是有
,于是有
 故应填2.
故应填2.
9.设非零复数 满足
满足 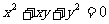 ,则代数式
,则代数式  的值是____________.
的值是____________.
讲解 将已知方程变形为  ,
,
解这个一元二次方程,得

显然有 , 而
, 而 ,于是
,于是
原式=
=
=
在上述解法中,“两边同除”的手法达到了集中变量的目的,这是减少变元的一个上策,值得重视.
8. 设复数 在复平面上对应向量
在复平面上对应向量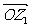 ,
, 将
将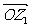 按顺时针方向旋转
按顺时针方向旋转 后得到向量
后得到向量 ,
, 对应的复数为
对应的复数为 ,则
,则
讲解 应用复数乘法的几何意义,得

 ,
,
于是 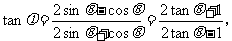
故应填 
7. 如果函数 的图象关于直线
的图象关于直线 对称,那么
对称,那么
讲解 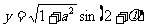 ,其中
,其中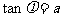 .
.

 是已知函数的对称轴,
是已知函数的对称轴,
 ,
,
即 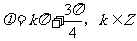 ,
,
于是  故应填
故应填  .
.
在解题的过程中,我们用到如下小结论:
函数 和
和 的图象关于过最值点且垂直于x轴的直线分别成轴对称图形.
的图象关于过最值点且垂直于x轴的直线分别成轴对称图形.
6. 不等式 (
(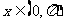 )的解集为
)的解集为 .
.
讲解 注意到 ,于是原不等式可变形为
,于是原不等式可变形为

而 ,所以
,所以 ,故应填
,故应填
5. 已知点P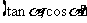 在第三象限,则角
在第三象限,则角 的终边在第
的终边在第 象限.
象限.
讲解 由已知得

从而角 的终边在第二象限,故应填二.
的终边在第二象限,故应填二.
4. 果函数 ,那么
,那么
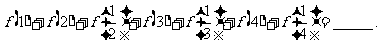
讲解 容易发现 ,这就是我们找出的有用的规律,于是
,这就是我们找出的有用的规律,于是
原式= ,应填
,应填
本题是2002年全国高考题,十分有趣的是,2003年上海春考题中也有一道类似题:
设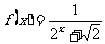 ,利用课本中推导等差数列前n项和的公式的方法,可求得
,利用课本中推导等差数列前n项和的公式的方法,可求得

3. 若函数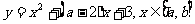 的图象关于直线
的图象关于直线 对称,则
对称,则
讲解 由已知抛物线的对称轴为 ,得
,得  ,而
,而 ,有
,有 ,故应填6.
,故应填6.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com