2．(2004湖南)设集合

，那么点P(2，3)的充要条件是(　 )

　　　　　　　　　 A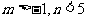．　　　　　　　　　　 B．

　　　　　　　　　 C．　　　　　　　　　　 D．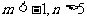

1．(2004湖北)函数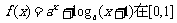上的最大值和最小值之和为a，则a的值为　　　　　　　　　　　　　　　　　　　　　　　 ( 　)

　　　　　　　 A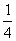．　　　　　　　 B．　　　　　　 C．2　　　 D．4

4．利用不等式解应用题的基本步骤：

(1)审题，(2)建模(不等式或函数)，(3)求解，(4)作答

3．不等式的应用范围十分广泛，许多问题，最终都可归结为不等式的求解、证明或求最值。这类问题大致可以分为两类：一类是建立不等式、解不等式；另一类是建立函数式求最大值或最小值．

2．解不等式与函数、数列、三角函数、解析几何综合问题的关键是找出各部分的知识点和解法，充分利用相关的知识和方法求解，要依据题设、题断的结构特点、内在联系、选择适当的解决方案，最终归结为不等式的求解、证明或求最值值问题．

1．不等式的性质，解法和证明方法，是综合运用不等式知识解决问题的基础。

4．通过不等式的基本知识、基本方法在代数、三角函数、数列、立体几何、解析几何等各部分知识中的应用，深化数学知识间的融汇贯通，从而提高分析问题解决问题的能力，提高数学素质及创新意识．

3．能从实际问题中抽象出数学模型，找出已知量与未知量，建立数学关系式，并用适当的方法解决问题

2．掌握利用均值不等式和函数单调性求最值的方法，正确理解恒正、恒负、解集为R、解集为空集的实际含义并会等价转换。

1．熟练运用不等式的知识综合解决函数、方程、数列、解析几何等有关问题