
(三)导函数
由函数 在
在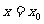 处求导数的过程可以看到,当
处求导数的过程可以看到,当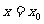 时,
时, 是一个确定的数,那么,当
是一个确定的数,那么,当 变化时,便是
变化时,便是 的一个函数,我们叫它为
的一个函数,我们叫它为 的导函数.
的导函数.
记作: 或
或 ,即
,即 .
.
注: 在不致发生混淆时,导函数也简称导数.
(二)导数的几何意义
函数 在
在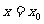 处的导数等于在该点
处的导数等于在该点 处的切线的斜率,
处的切线的斜率,
即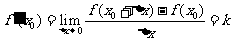
说明: 求曲线在某点处的切线方程的基本步骤:
①求出 点的坐标;
点的坐标;
②求出函数在点 处的变化率
处的变化率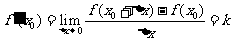 得到曲线在点
得到曲线在点 的切线的斜率;
的切线的斜率;
③利用点斜式求切线方程.
(一)曲线的切线及切线的斜率
如图3.1-2,当 沿着曲线
沿着曲线 趋近于点
趋近于点 时,割线
时,割线 的变化趋势是什么?
的变化趋势是什么?








我们发现,当点 沿着曲线无限接近点
沿着曲线无限接近点 即
即 时,割线
时,割线 趋近于确定的位置,这个确定位置的直线
趋近于确定的位置,这个确定位置的直线 称为曲线在点
称为曲线在点 处的切线.
处的切线.
问题: (1)割线 的斜率
的斜率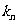 与切线
与切线 的斜率
的斜率 有什么关系?
有什么关系?
(2)切线 的斜率
的斜率 为多少?
为多少?
容易知道,割线 的斜率是
的斜率是 ,当点
,当点 沿着曲线无限接近点
沿着曲线无限接近点 时,
时,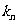 无限趋近于切线
无限趋近于切线 的斜率
的斜率 ,即
,即

说明: (1)设切线的倾斜角为 ,
,
那么当 时,割线
时,割线 的斜率,称为曲线在点
的斜率,称为曲线在点 处的切线的斜率.
处的切线的斜率.
这个概念: ①提供了求曲线上某点切线的斜率的一种方法;
②切线斜率的本质-函数在 处的导数.
处的导数.
(2)曲线在某点处的切线:
1)与该点的位置有关;
2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;
3)曲线切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多.
(二)瞬时速度、导数
我们知道,导数表示函数 在
在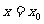 处的瞬时变化率,反映了函数
处的瞬时变化率,反映了函数 在
在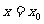 附近的变化情况,导数
附近的变化情况,导数 的几何意义是什么呢?
的几何意义是什么呢?
(一)平均变化率、割线的斜率
20.解:设事件 为“方程
为“方程 有实根”.
有实根”.
当 ,
, 时,方程
时,方程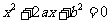 有实根的充要条件为
有实根的充要条件为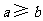 .
.
(Ⅰ)基本事件共12个:
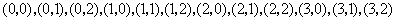 .其中第一个数表示
.其中第一个数表示 的取值,第二个数表示
的取值,第二个数表示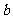 的取值.
的取值.
事件 中包含9个基本事件,事件
中包含9个基本事件,事件 发生的概率为
发生的概率为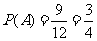 .
.
(Ⅱ)试验的全部结束所构成的区域为 .
.
构成事件 的区域为
的区域为 .
.
所以所求的概率为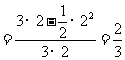 .
.
19.解:设 表示一个基本事件,则掷两次骰子包括:
表示一个基本事件,则掷两次骰子包括: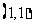 ,
,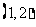 ,
, ,
,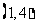 ,
, ,
, ,
,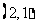 ,
, ,……,
,……,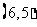 ,
, ,共36个基本事件.
,共36个基本事件.
(1)用 表示事件“
表示事件“ ”,则
”,则 的结果有
的结果有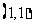 ,
,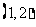 ,
,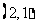 ,共3个基本事件.
,共3个基本事件.
∴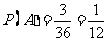 .
.
答:事件“ ”的概率为
”的概率为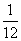 .
.
(2)用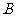 表示事件“
表示事件“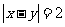 ”,
”,
则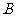 的结果有
的结果有 ,
, ,
, ,
, ,
,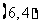 ,
,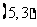 ,
,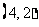 ,
,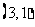 ,共8个基本事件. ∴
,共8个基本事件. ∴ .
.
答:事件“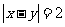 ”的概率为
”的概率为 .
.
18.解:(Ⅰ)从8人中选出日语、俄语和韩语志愿者各1名,其一切可能的结果组成的基本事件空间 {
{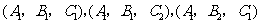 ,
, ,
,
 ,
,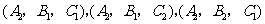 ,
, ,
,
 ,
, ,
, ,
,
 }
}
由18个基本事件组成.由于每一个基本事件被抽取的机会均等,因此这些基本事件的发生是等可能的.
用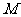 表示“
表示“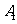 恰被选中”这一事件,则
恰被选中”这一事件,则 {
{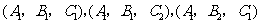 ,
,
 },事件
},事件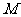 由6个基本事件组成,
由6个基本事件组成,
因而 .
.
(Ⅱ)用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,由于
全被选中”这一事件,由于 {
{ },事件
},事件 有3个基本事件组成,
有3个基本事件组成,
所以 ,由对立事件的概率公式得
,由对立事件的概率公式得 .
.
17.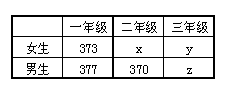 解: (1)由
解: (1)由 ,解得
,解得 ,
,
(2)初三年级人数为 ,
,
设应在初三年级抽取m人,则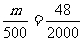 ,解得m=12.
,解得m=12.
答: 应在初三年级抽取12名.
(3)设初三年级女生比男生多的事件为 ,初三年级女生和男生数记为数对
,初三年级女生和男生数记为数对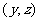 ,
,
由(2)知 ,则基本事件总数有:
,则基本事件总数有:
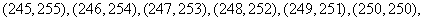
 共11个,
共11个,
而事件 包含的基本事件有:
包含的基本事件有:
 共5个,
共5个,
∴
16、解:(Ⅰ)总体平均数为 .
.
(Ⅱ)设 表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”.
表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”.
从总体中抽取2个个体全部可能的基本结果有: ,
,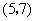 ,
,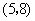 ,
,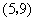 ,
, ,
,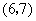 ,
, ,
,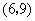 ,
, ,
,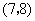 ,
,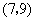 ,
, ,
, ,
, ,
,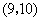 .共15个基本结果.
.共15个基本结果.
事件 包括的基本结果有:
包括的基本结果有: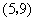 ,
, ,
, ,
,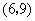 ,
, ,
,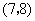 ,
,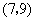 .共有7个基本结果.所以所求的概率为
.共有7个基本结果.所以所求的概率为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com