
2.按照要求,将下列词语或短语组成句子,不能增删词语。
中山大学文科楼 主题 在
“诗词格律及吟诵” 陈永正教授
的 举行 是 讲座
强调内容:_______________________
强调人物:________________________
[答案] (强调内容:)陈永正教授在中山大学文科楼举行的讲座主题是“诗词格律及吟诵”。
(强调人物:)在中山大学文科楼举行“诗词格律及吟诵”主题讲座的是陈永正教授。(或:是陈永正教授在中山大学文科楼举行“诗词格律及吟诵”主题讲座的。)
1.(2010年合肥第一次质检)某班学生在讨论“说不尽的贾宝玉”时,从不同角度简要地阐述了他们对贾宝玉的认识。请你将其整合为一个长句,可以适当增删词语。
①贾宝玉是个贵族公子。
②贾宝玉生活在充满矛盾的封建大家庭。
③叛逆精神是贾宝玉的性格特征。
④曹雪芹写《红楼梦》是为了揭示贾府的衰亡史和罪恶史。
⑤贾宝玉是封建伦理的孤独的反抗者。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
[解析] 将短句变为长句,第一步要确定一个句子作为长句的主干,这个句子常常是一组短句中的肯定性判断句或结论性语句,因此我们基本可以判定①是主干句。第二步是把其余短句转化为短语,如②转化成短语就是“生活在充满矛盾的封建大家庭里的贾宝玉”,③转化为“具有叛逆精神的贾宝玉”,④转化为“曹雪芹为揭示贾府的衰亡史和罪恶史所写的《红楼梦》”,⑤转化为“孤独地反抗着封建伦理的贾宝玉”。第三步就是将这些短语加入到主干句中,这些短语都是修饰限制“贾宝玉”的,做的都是“贾宝玉”的定语,在加入主干句时要注意这些定语的次序,使其顺序恰当,合情合理。
[答案] 示例:贾宝玉是曹雪芹为揭示贾府的衰亡史和罪恶史所写的《红楼梦》中生活在充满矛盾的封建大家庭里的具有叛逆精神的孤独地反抗着封建伦理的贵族公子。
12.已知函数f(x)=ax2+bx+c(a>0,b∈R,c∈R).
(1)若函数f(x)的最小值是f(-1)=0,且c=1,
F(x)=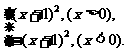 求F(2)+F(-2)的值;
求F(2)+F(-2)的值;
(2)若a=1,c=0,且|f(x)|≤1在区间(0,1]恒成立,试求b的取值范围.
解:(1)由已知c=1,f(-1)=a-b+c=0,且-=-1,解得a=1,b=2.
∴f(x)=(x+1)2.
∴F(x)=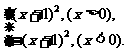
∴F(2)+F(-2)=(2+1)2+[-(-2+1)2]=8.
(2)由题知f(x)=x2+bx,原命题等价于-1≤x2+bx≤1在x∈(0,1]恒成立,即b≤-x且b≥--x在x∈(0,1]恒成立,
根据单调性可得-x的最小值为0,
--x的最大值为-2,
所以-2≤b≤0.
11.规定记号“*”表示一种运算,即a*b=+a+b,a,b是正实数,已知1];
(2)函数f(x)=k*x的值域是 .
解析:(1)1]k)+1+k=3,解得k=1.
(2)f(x)=k*x=1]x)+1+x≥1.
答案:(1)1 (2)[1,+∞)
10.设f(x)= 若f(g(x))的值域是[0,+∞),则函数y=g(x)的值域是 ( )
若f(g(x))的值域是[0,+∞),则函数y=g(x)的值域是 ( )
A.(-∞,-1]∪[1,+∞) B.(-∞,-1]∪[0,+∞)
C.[0,+∞) D.[1,+∞)

解析:如图为f(x)的图象,由图象知f(x)的值域为(-1,+∞),
若f(g(x))的值域是[0,+∞),只需g(x)∈(-∞,-1]∪[0,+∞).
答案:B
8.分别求下列函数的值域:
(1)y=;
(2)y=-x2+2x(x∈[0,3]);
(3)y=x+;
(4)y=.
解:(1)分离变量法将原函数变形为
y==2+.
∵x≠3,∴≠0.
∴y≠2,即函数值域为{y|y∈R且y≠2}.
(2)配方法
∵y=-(x-1)2+1,根据二次函数的性质,可得原函数的值域是[-3,1].
(3)换元法
先考虑函数定义域,由1-x2≥0,得-1≤x≤1,设x=cosθ(θ∈[0,π]),则y=sinθ+cosθ=sin(θ+),易知当θ=时,y取最大值为,当θ=π时,y取最小值为-1,
∴原函数的值域是[-1,].
(4)分离常数法
y=
∵1+2x>1,∴0< <2,
<2,
∴-1<-1+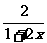 <1,∴所求值域为(-1,1).
<1,∴所求值域为(-1,1).
|
题组三 |
函数定义域和值域的综合问题 |
 9.(2010·福建“四地六校”联考)设集合A=[0,),B=[,1],函数f (x)=
9.(2010·福建“四地六校”联考)设集合A=[0,),B=[,1],函数f (x)= 若x0∈A,且f
[f (x0)]
∈A,则x0的取值范围是
( )
若x0∈A,且f
[f (x0)]
∈A,则x0的取值范围是
( )
A.(0,] B.[,] C.(,) D.[0,]
解析:∵0≤x0<,∴f(x0)=x0+∈[,1)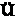 B,
B,
∴f[f(x0)]=2(1-f(x0))=2[1-(x0+)]=2(-x0).
∵f[f(x0)]∈A,∴0≤2(-x0)<.
∴<x0≤,又∵0≤x0<,∴<x0<.
答案:C
7.(2010·珠海模拟)若函数y=f(x)的值域是[1,3],则函数F(x)=1-2f(x+3)的值域是 .
解析:∵1≤f(x)≤3,
∴-6≤-2f(x+3)≤-2,
∴-5≤1-2f(x+3)≤-1,
即F(x)的值域为[-5,1].
答案:[-5,1]
6.对a,b∈R,记max{a,b}= .函数f(x)=max{|x+1|,|x-2|}(x∈R)的最小
.函数f(x)=max{|x+1|,|x-2|}(x∈R)的最小
值是 ( )
A.0 B. C. D.3
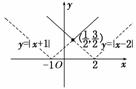
解析:函数f(x)=max{|x+1|,|x-2|}(x∈R)的图象如图所示,
由图象可得,其最小值为.
答案:C
5.若函数y=f(x)的值域是[,3],则函数F(x)=f(x)+的值域是
A.[,3] B.[2,] C.[,] D.[3,]
解析:令t=f(x),则≤t≤3,由函数g(t)=t+在区间[,1]上是减函数,在[1,3]上是增函数,则g()=,g(1)=2,g(3)=,故值域为[2,].
答案:B
4.若函数f(x)=(a2-2a-3)x2+(a-3)x+1的定义域和值域都为R,则a的取值范围是( )
A.a=-1或3 B.a=-1
C.a>3或a<-1 D.-1<a<3
解析:若a2-2a-3≠0,则函数为二次函数,不可能定义域和值域都为R,当a2-2a-3=0时,得a=-1或3,但当a=3时,函数为常数函数,也不可能定义域和值域都为R,故a=-1.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com