
分步设问类比推理、列表归纳类比推理,既要理解加速度概念,又要理解状态量的变化率。培养学生运用推理方法和数学工具解决物理问题的能力。
认识图像要引导回顾实验操作中纸带运动、建立坐标系、描点等过程,如如何根据v-t图像判断速度方向?
如何判断一些似是而非的说法,即要根据定义公式,又要举例增强说法力。
加速度是矢量,判断是加速还是减速,要引导同学充分表达,充分暴露错误的想法,并做好总结归纳。可以补充有往复的直线运动。
(三)课堂内容小结
类比法,加速度的物理意义、定义式、方向。
(三)教学重点、难点
1.教学重点及其教学策略
理解加速度的定义与方向。
通过类比法,用比值法定义加速度,画图表示速度、速度变化、加速度矢量的方向。
2.教学难点及其教学策略
用比值法定义加速度,画图表示速度、速度变化、加速度矢量的方向。
用类比法,体会数学公式、有向线段解决物理问题的意义。
(二)教学目标
1.观察实验2测量瞬时速度的数据,列举生活中速度变化的例子,感受速度变化、速度变化快慢与位置变化及其变化快慢是两件具有不同的物理意义的事件,认识引入加速度概念的物理意义。
2.选择典型例子、探究表示速度变化快慢的方法,类比位置、位置变化、位置变化快慢……用比值法定义加速度。
3.类比用有向线段表示位置、位置变化、速度矢量的方向,画图表示速度、速度变化、加速度矢量的方向。
4.理解加速度的定义与方向,体会应用数学公式、有向线段解决物理问题的意义,培养应用数学工具解决物理问题的技能。
5.经历分析速度-时间图像,探究数学图像的物理意义及其方法,体会应用数学图像解决物理问题的意义,培养应用数学工具解决物理问题的技能。
(一)课程与学情分析
在共同必修模块物理1的内容标准中涉及本节的内容有“经历…实验研究的过程,理解…加速度,…”。加速度是学习匀变速直线运动规律和进一步学习其它各种变速运动的基础;定义加速度所应用的比值法以及极限法等都是物理学中常用的研究方法。
学生对速度变化及其快慢的感知缺乏直接经验的支持,并与运动的快慢(位置变化快慢)混淆不清,通过丰富的实例、充分表达交流感受速度的变化快慢与运动快慢是两个具有不同意义的物理事件,类比并迁移应用比值法定义加速度,类比并迁移用有向线段表示位置、位置变化(位移)、位置变化快慢(速度)、速度变化、速度变化快慢的矢量方向,既要防范错误概念又要体会变化率的物理意义。
20、已知函数 图象上一点
图象上一点 处的切线方程为
处的切线方程为
 . (Ⅰ)求
. (Ⅰ)求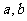 的值;
的值;
(Ⅱ)若方程 在
在 内有两个不等实根,求
内有两个不等实根,求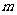 的取值范围(其中
的取值范围(其中 为自然对数的底数,
为自然对数的底数, );
);
(Ⅲ)令 ,如果
,如果 图象与
图象与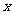 轴交于
轴交于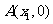 ,
,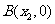 (
( ),
), 中点为
中点为 ,求证:
,求证: 在
在 处的导数
处的导数 .
.
解:(Ⅰ) ,
, ,
, .
.
∴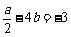 ,且
,且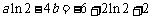 . …………………… 2分
. …………………… 2分
解得 .
…………………… 3分
.
…………………… 3分
(Ⅱ) ,令
,令 ,
,
则 ,令
,令 ,得
,得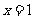 (
( 舍去).
舍去).
在 内,当
内,当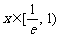 时,
时,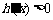 , ∴
, ∴  是增函数;
是增函数;
当 时,
时, , ∴
, ∴  是减函数 …………………… 5分
是减函数 …………………… 5分
则方程 在
在 内有两个不等实根的充要条件是
内有两个不等实根的充要条件是 …………7分
…………7分
即 . …………………………… 8分
. …………………………… 8分
(Ⅲ) ,
,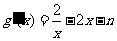 .
.
假设结论成立,则有 ………………………… 9分
………………………… 9分
①-②,得 .
.
∴ . …………………………………………………… 10分
. …………………………………………………… 10分
由④得 ,
,
∴ .即
.即 .
.
即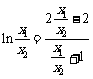 .⑤
…………………………………………………… 11分
.⑤
…………………………………………………… 11分
令 ,
,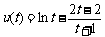 (
(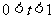 ), …………………………………… 12分
), …………………………………… 12分
则 >0.∴
>0.∴ 在
在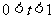 上增函数, ∴
上增函数, ∴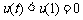 , ……… 14分
, ……… 14分
∴⑤式不成立,与假设矛盾.
19、函数 的定义域为
的定义域为 ,并满足条件:① 对任意
,并满足条件:① 对任意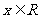 ,有
,有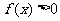 ;
;
② 对任意 ,有
,有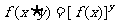 ;③
;③  .
.
(1)求 的值; (2)求证:
的值; (2)求证: 在
在 上是单调递增函数;
上是单调递增函数;
解:(1)令 ,则
,则

(2)任取 ,且
,且
设 ,则
,则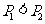

 ,
,

 ,
,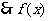 在
在 上是单调递增函数
上是单调递增函数
18、(14分)随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员
人(140< <420,且
<420,且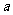 为偶数),每人每年可创利
为偶数),每人每年可创利 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利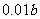 万元,但公司需付下岗职员每人每年
万元,但公司需付下岗职员每人每年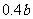 万元的生活费,并且该公司正常运转所需人数不得小于现有职员的
万元的生活费,并且该公司正常运转所需人数不得小于现有职员的 ,为获得最大的年经济效益,该公司应裁员多少人?
,为获得最大的年经济效益,该公司应裁员多少人?
解:设裁员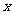 人,可获得的经济效益为
人,可获得的经济效益为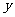 万元,则
万元,则
 =
=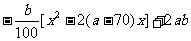
依题意  ≥
≥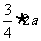 , ∴0<
, ∴0<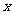 ≤
≤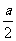 .
.
又140< <420, 70<
<420, 70<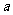 <210.
<210.
① 当0< ≤
≤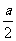 ,即70<
,即70<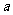 ≤140时,
≤140时,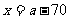 ,
, 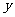 取到最大值;
取到最大值;
② 当 >
>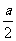 ,即140<
,即140<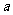 <210时,
<210时, ,
, 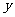 取到最大值;
取到最大值;
答:当70<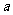 ≤140时,应裁员
≤140时,应裁员 人;当140<
人;当140<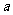 <210时,应裁员
<210时,应裁员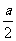 人.
人.
17、(14分)已知函数f(x)=2x3+ax2+bx+3在x=-1和x=2处取得极值.
(1)求f(x)的表达式和极值.
(2)若f(x)在区间[m,m+4]上是单调函数,试求m的取值范围.
解:(1)
由已知有 ,即
,即 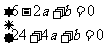
 解得
解得

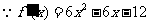
由 解得
解得 
由 解得
解得 
故函数f(x)在 和
和 是增函数,在
是增函数,在 上是减函数;
上是减函数;
当 时,有极大值10 , 当
时,有极大值10 , 当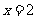 时,有极小值
时,有极小值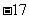
(2)由(1)可知,要使f(x)在区间[m,m+4]上是单调函数时,须
 或
或
 或
或

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com