10. 设斜率为2的直线过抛物线的焦点F,且和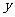轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为(　　 ). 　 　

A.　　 B.　　 C. 　　　D.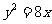

[解析]: 抛物线的焦点F坐标为,则直线的方程为,它与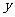轴的交点为A,所以△OAF的面积为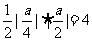,解得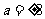.所以抛物线方程为,故选B. 　 　

答案:B.

[命题立意]:本题考查了抛物线的标准方程和焦点坐标以及直线的点斜式方程和三角形面积的计算.考查数形结合的数学思想,其中还隐含着分类讨论的思想,因参数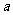的符号不定而引发的抛物线开口方向的不定以及焦点位置的相应变化有两种情况,这里加绝对值号可以做到合二为一.

9. 已知α，β表示两个不同的平面，m为平面α内的一条直线，则“”是“”的(　　　　　 )

A.充分不必要条件　　　　 B.必要不充分条件

C.充要条件　　　　 　　　D.既不充分也不必要条件　 　

[解析]:由平面与平面垂直的判定定理知如果m为平面α内的一条直线,,则,反过来则不一定.所以“”是“”的必要不充分条件　 　.

答案:B.

[命题立意]:本题主要考查了立体几何中垂直关系的判定和充分必要条件的概念.

8.设P是△ABC所在平面内的一点，，则(　　)

A.　　 B. 　　C. 　　D.

[解析]:因为，所以点P为线段AC的中点，所以应该选B。

答案：B.

[命题立意]:本题考查了向量的加法运算和平行四边形法则，　 　

可以借助图形解答。

7. 定义在R上的函数f(x)满足f(x)= 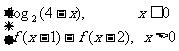，则f(3)的值为(　　　 )

A.-1　　　　　 B. -2　　　　 C.1　　　　 D. 2

[解析]:由已知得,,,

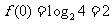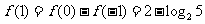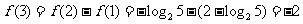,,故选B.

答案:B. 　 　

[命题立意]:本题考查对数函数的运算以及推理过程..

6. 函数的图像大致为(　　　　 ). 　 　

[解析]:函数有意义,需使,其定义域为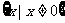,排除C,D,又因为,所以当时函数为减函数,故选A. 　 　

答案:A.

[命题立意]:本题考查了函数的图象以及函数的定义域、值域、单调性等性质.本题的难点在于给出的函数比较复杂,需要对其先变形,再在定义域内对其进行考察其余的性质.

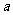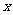5.在R上定义运算⊙: ⊙,则满足⊙<0的实数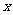的取值范围为(　　 ).

A.(0,2)　　 B.(-2,1)　　 C.　　　 D.(-1,2) 　 　

[解析]:根据定义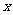⊙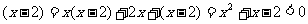,解得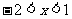,所以所求的实数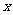的取值范围为(-2,1),故选B.

答案:B.

[命题立意]:本题为定义新运算型,正确理解新定义是解决问题的关键,译出条件再解一元二次不等式.

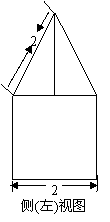
4. 一空间几何体的三视图如图所示,则该几何体的体积为(　　　　 ).

A.　　　 B. 　　　　　　C. 　　　　　D.

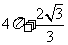
[解析]:该空间几何体为一圆柱和一四棱锥组成的,

圆柱的底面半径为1,高为2,体积为,四棱锥的底面

边长为，高为，所以体积为

所以该几何体的体积为. 　 　

答案:C

[命题立意]:本题考查了立体几何中的空间想象能力,

由三视图能够想象得到空间的立体图,并能准确地

计算出.几何体的体积. 　 　

3. [解析]:将函数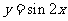的图象向左平移个单位,得到函数即的图象,再向上平移1个单位,所得图象的函数解析式为,故选A.

答案:A

[命题立意]:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.

3.将函数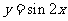的图象向左平移个单位, 再向上平移1个单位,所得图象的函数解析式是(　　　　　 ). 　 　

A. 　　　　B. 　　C.　　 D.

2. [解析]: 　,故选C.

答案:C

[命题立意]:本题考查复数的除法运算，分子、分母需要同乘以分母的共轭复数，把分母变为实数，将除法转变为乘法进行运算.