
1.核酸是生物体内的重要物质,在生物体内是
A.承担生命活动的物质 B.携带遗传信息的物质
C.细胞内的能源物质 D.细胞的结构物质
(16)(本小题满分12分)
在 ABC中,C-A=
ABC中,C-A= , sinB=
, sinB= 。
。
(I)求sinA的值;
(II)设AC= ,求
,求 ABC的面积
ABC的面积
(17)(本小题满分12分)
某良种培育基地正在培育一种小麦新品种A,将其与原有的一个优良品种B进行对照
试验,两种小麦各种植了25亩,所得亩产数据(单位:千克)如下
品种A:357,359,367,368,375,388,392,399,400,405,414,
415,421,423,423,427,430,430,434,443,445,451,454
品种B:363,371,374,383,385,386,391,392,394,394,395,397
397,400,401,401,403,406,407,410,412,415,416,422,430
(I)完成所附的茎叶图
(II)用茎叶图处理现有的数据,有什么优点?
(III)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论。
(18)(本小题满分12分)
已知椭圆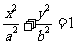 (a>b>0)的离心率为
(a>b>0)的离心率为 ,以原点为圆心、椭圆短半轴长半径的
,以原点为圆心、椭圆短半轴长半径的
圆与直线y=x+2相切,
(I)求a与b;
(II)设该椭圆的左,右焦点分别为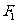 和
和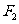 ,直线
,直线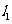 过
过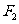 且与x轴垂直,动直线
且与x轴垂直,动直线 与y
与y
轴垂直, 交
交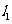 与点P. 求线段P
与点P. 求线段P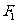 垂直平分线与
垂直平分线与 的交点M的轨迹方程,并
的交点M的轨迹方程,并
指明曲线类型。
(19)(本小题满分12分)
已知数列{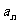 } 的前n项和
} 的前n项和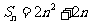 ,数列{
,数列{ }的前n项和
}的前n项和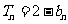
(I)求数列{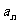 }与{
}与{ }的通项公式;
}的通项公式;
 (II)设
(II)设 ,证明:当且仅当n≥3时,
,证明:当且仅当n≥3时,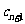 <
<
(20)(本小题满分13分)
如图,ABCD的边长为2的正方形,直线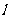 与平
与平
面ABCD平行,E和F式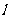 上的两个不同点,且
上的两个不同点,且
EA=ED,FB=FC,  和
和 是平面ABCD内的两
是平面ABCD内的两
点, 和
和
 都与平面ABCD垂直,
都与平面ABCD垂直,
(I)证明:直线 垂直且平分线段AD:
垂直且平分线段AD:
(II)若∠EAD=∠EAB= ,EF=2,求多面
,EF=2,求多面
体ABCDEF的体积。
(21)(本小题满分14分)
已知函数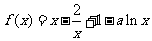 ,a>0,
,a>0,
(I)讨论 的单调性;
的单调性;
(II)设a=3,求 在区间{1,
在区间{1,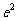 }上值域。期中e=2.71828…是自然对数的底数。
}上值域。期中e=2.71828…是自然对数的底数。
(11)若随机变量 -
-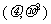 ,则
,则 =________.
=________.
 (12)以直角坐标系的原点为极点,
(12)以直角坐标系的原点为极点, 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位。已知直线的极坐标方程为
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位。已知直线的极坐标方程为 ,它与曲线
,它与曲线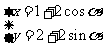 (
( 为参数)相交于两点A和B,则|AB|=_______.
为参数)相交于两点A和B,则|AB|=_______.
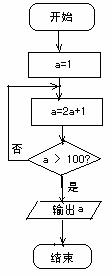
(13) 程序框图(即算法流程图)如图所示,其输出结果是_______.
(14)给定两个长度为1的平面向量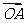 和
和 ,它们的夹角为
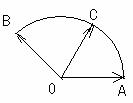
,它们的夹角为 .如图所示,点C在以O为圆心的圆弧AB上变动.若
.如图所示,点C在以O为圆心的圆弧AB上变动.若 其中
其中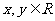 ,则
,则 的最大值是=________.
的最大值是=________.
(15)对于四面体ABCD,下列命题正确的是_________
(写出所有正确命题的编号)。
1相对棱AB与CD所在的直线是异面直线;
2由顶点A作四面体的高,其垂足是 BCD的三条高线的交点;
BCD的三条高线的交点;
3若分别作 ABC和
ABC和 ABD的边AB上的高,则这两条高所在直线异面;
ABD的边AB上的高,则这两条高所在直线异面;
4分别作三组相对棱中点的连线,所得的三条线段相交于一点;
5最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱。
(1)i是虚数单位,若 ,则乘积
,则乘积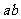 的值是
的值是
(A)-15
(B)-3 (C)3 (D)15
(2)若集合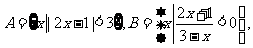 则A∩B是
则A∩B是
(A)  (B)
(B) 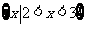

(C)  (D)
(D) 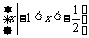

(3)下列曲线中离心率为 的是
的是
(A)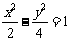 (B)
(B) (C)
(C) (D)
(D)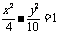

(4)下列选项中,p是q的必要不充分条件的是
(A)p: >b+d
, q:
>b+d
, q: >b且c>d
>b且c>d

(B)p:a>1,b>1 q: 的图像不过第二象限
的图像不过第二象限
(C)p: x=1,
q:

(D)p:a>1,
q:  在
在 上为增函数
上为增函数
(5)已知 为等差数列,
为等差数列,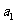 +
+ +
+ =105,
=105,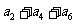 =99,以
=99,以 表示
表示 的前
的前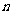 项和,则使得
项和,则使得 达到最大值的
达到最大值的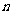 是
是
(A)21
(B)20 (C)19 (D) 18
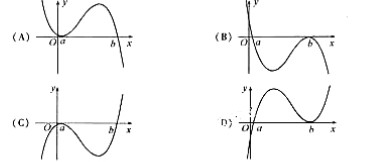
(6)设 <b,函数
<b,函数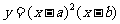 的图像可能是
的图像可能是

(7)若不等式组 所表示的平面区域被直线
所表示的平面区域被直线 分为面积相等的两部分,则
分为面积相等的两部分,则 的值是
的值是
(A)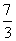 (B)
(B)
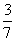 (C)
(C) (D)
(D) 

(8)已知函数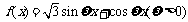 ,
, 的图像与直线
的图像与直线 的两个相邻交点的距离等于
的两个相邻交点的距离等于 ,则
,则 的单调区间是
的单调区间是
(A) (B)
(B)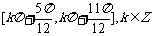

(C) (D)
(D)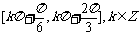

(9)已知函数 在R上满足
在R上满足 ,则曲线
,则曲线 在点
在点 处的切线方程是
处的切线方程是
(A) (B)
(B) (C)
(C)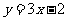 (D)
(D)

(10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于
(A) (B)
(B) 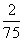 (C)
(C)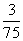 (D)
(D)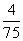
25.若P为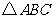 所在平面上一点,且
所在平面上一点,且 ,则点
,则点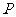 叫做
叫做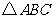 的费马点.
的费马点.
 (1)若点
(1)若点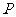 为锐角
为锐角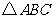 的费马点,且
的费马点,且 ,则
,则 的值为________;
的值为________;
(2)如图,在锐角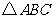 外侧作等边
外侧作等边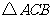 ′连结
′连结 ′.
′.
求证: ′过
′过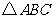 的费马点
的费马点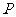 ,且
,且 ′=
′= .
.
浙江省2009年初中毕业生学业考试(湖州市)
24.(本小题12分)
已知抛物线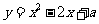 (
( )与
)与 轴相交于点
轴相交于点 ,顶点为
,顶点为 .直线
.直线 分别与
分别与 轴,
轴, 轴相交于
轴相交于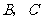 两点,并且与直线
两点,并且与直线 相交于点
相交于点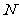 .
.
(1)填空:试用含 的代数式分别表示点
的代数式分别表示点 与
与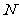 的坐标,则
的坐标,则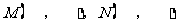 ;
;
(2)如图,将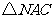 沿
沿 轴翻折,若点
轴翻折,若点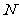 的对应点
的对应点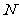 ′恰好落在抛物线上,
′恰好落在抛物线上,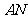 ′与
′与 轴交于点
轴交于点 ,连结
,连结 ,求
,求 的值和四边形
的值和四边形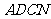 的面积;
的面积;
(3)在抛物线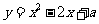 (
( )上是否存在一点
)上是否存在一点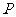 ,使得以
,使得以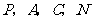 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出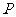 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.

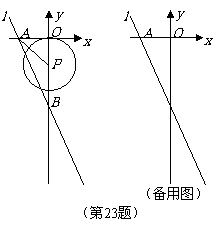
23.(本小题10分)
如图,在平面直角坐标系中,直线 ∶
∶ =
= 分别与
分别与 轴,
轴, 轴相交于
轴相交于 两点,点
两点,点 是
是 轴的负半轴上的一个动点,以
轴的负半轴上的一个动点,以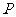 为圆心,3为半径作
为圆心,3为半径作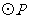 .
.
(1)连结 ,若
,若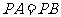 ,试判断
,试判断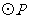 与
与 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(2)当 为何值时,以
为何值时,以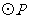 与直线
与直线 的两个交点和圆心
的两个交点和圆心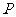 为顶点的三角形是正三角形?
为顶点的三角形是正三角形?
22.(本小题10分)
随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2006年底拥有家庭轿车64辆,2008年底家庭轿车的拥有量达到100辆.
(1) 若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2009年底家庭轿车将达到多少辆?
(2) 为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
21.(本小题10分)
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为 四等,并绘制成下面的频数分布表和扇形统计图.
四等,并绘制成下面的频数分布表和扇形统计图.

(1)试直接写出 的值;
的值;
(2)求表示得分为 等的扇形的圆心角的度数;
等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到 等和
等和 等的人数共有多少人?
等的人数共有多少人?
20.(本小题8分)
如图:已知在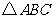 中,
中,
 ,
, 为
为 边的中点,过点
边的中点,过点 作
作 ,
,
 垂足分别为
垂足分别为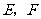 .
.
(1) 求证: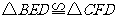 ;
;
(2)若 ,求证:四边形
,求证:四边形 是正方形.
是正方形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com