
3.解答选择题时,请将选项的字母代号写在答题表一内;解答填空题时,请将答案写在答题表二内;做解答题、证明题、应用题、分析题、探究题时,请将解答过程和结果写在指定的位置上.
阅卷人答题表一
每小题给出4个答案,其中只有一个是正确的.请把正确答案的字母代号填在上面的答题表一内.
2.答题前,请将考场号、试室号、座位号、考生号、姓名写在试卷密封线内.不得在试卷上作任何标记.
3、存 在 性 探 究 题
 例1、如图,在△ABC中,BC=6,AC=
例1、如图,在△ABC中,BC=6,AC= ,∠ACB=45°,在BC边上有一动点M,过M作MN∥AB,与AC交于点N,连结AM,设BM
,∠ACB=45°,在BC边上有一动点M,过M作MN∥AB,与AC交于点N,连结AM,设BM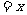
 0<
0<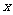 <6
<6 ,△AMN的面积为
,△AMN的面积为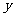 。(1)求
。(1)求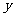 与
与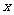 的函数关系式;
的函数关系式;
(2)是否存在这样的点M,使 =2:3?
=2:3?
若存在则求之,否则说明理由。
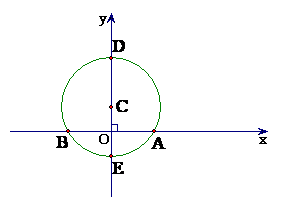
例2、已知:如图,在平面直角坐标系中,点C在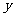 轴上,以C为圆心,4cm为半径的圆与
轴上,以C为圆心,4cm为半径的圆与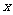 轴相交于点A、B,与
轴相交于点A、B,与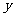 轴相交于D、E,且
轴相交于D、E,且 。点P是⊙C上一动点(P点与A、B点不重合)。连结BP、AP。
。点P是⊙C上一动点(P点与A、B点不重合)。连结BP、AP。
(1)求∠BPA的度数;
 (2)若过点P的⊙C的切线交
(2)若过点P的⊙C的切线交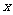 轴于点G,是否存在点P,使△APB与以A、G、P为顶点的三角形相似?
轴于点G,是否存在点P,使△APB与以A、G、P为顶点的三角形相似?
若存在,求出点P的坐标;若不存在,说明理由。
例3、(本小题满分8分)
探索下列问题:
(1)在图12-1给出的四个正方形中,各画出一条直线(依次是:水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线),将每个正方形都分割成面积相等的两部分;
(2)一条竖直方向的直线m以及任意的直线n,在由左向右平移的过程中,将正六边形分成左右两部分,其面积分别记为S1和S2.
①请你在图12-2中相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接);
②请你在图12-3中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接).

 (3)是否存在一条直线,将一个任意的平面图形(如图12-4)分割成面积相等的两部分,请简略说出理由.
(3)是否存在一条直线,将一个任意的平面图形(如图12-4)分割成面积相等的两部分,请简略说出理由.


2、条 件 探 究 题
条件探究题,一般是由给定的结论反过来探究命题成立应具备的条件。
 例1、已知:已知Rt△ABC中,∠C=90°,∠B的正切值是
例1、已知:已知Rt△ABC中,∠C=90°,∠B的正切值是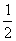 ,AC=3,点P为直线AC上的一点,当CP为何值时,
,AC=3,点P为直线AC上的一点,当CP为何值时,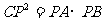 ?
?
 例2、已知:四边形ABCD是平行四边形,点A的坐标为(12,0),点C的坐标为(6,8),直线
例2、已知:四边形ABCD是平行四边形,点A的坐标为(12,0),点C的坐标为(6,8),直线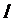 :
: 与
与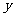 轴相交于点D。(1)当
轴相交于点D。(1)当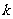 为何值时,直线
为何值时,直线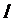 恰好平分平行四边形ABCD的面积?(2)若直线
恰好平分平行四边形ABCD的面积?(2)若直线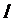 与线段CO、AO分别相交于点P、Q,
与线段CO、AO分别相交于点P、Q,
则当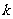 为何值时,△OPQ是等腰三角形?
为何值时,△OPQ是等腰三角形?
1、结 论 探 究 题
结论探究题,一般是由给定的已知条件探求相应的结论,解题时往往要求充分利用条件进行大胆而合理的猜想,发现规律,得出结论。
例1、有若干个数,第1个数记为 ,第2个数记为
,第2个数记为 ,第3个数记为
,第3个数记为 ,……,第
,……,第 个数记为
个数记为 ,若
,若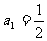 ,从第2个数起,每个数都等于“1与它前面的那个数的差的倒数”。
,从第2个数起,每个数都等于“1与它前面的那个数的差的倒数”。
(1)试计算: = ,
= , = ,
= , = ;
= ;
(2)根据以上计算结果,请你写出:
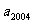 = ,
= , = 。
= 。
例2、水葫芦是一种水生飘浮植物,有着惊人的繁殖能力。据报现已造成某些流域河道堵塞,水质污染等严重后果。据研究表明:适量的水葫芦生长对水质的净化是有利的,关键是科学管理和转化利用。若在适宜条件下,1株水葫芦每5天就能新繁殖1株(不考虑植株死亡、被打捞等其它因素)。
(1)假设江面上现有一株水葫芦,填写下表:
|
第几天 |
5 |
10 |
15 |
… |
50 |
… |
5n |
|
总株数 |
2 |
4 |
|
|
|
|
|
(2)假设某流域内水葫芦维持在约33万株以内对净化水质有益。若现有10株水葫芦,请你尝试利用计算器进行估算探究,照上述生长速度,多少天时水葫芦约有33万株?此后就必须开始定期打捞处理水葫芦。(要求写出必要的尝试、估算过程!)
例3、如图,“取正方形各边的中点,并把相对的两个中点相连,这样把一个大正方形分成了四个小正方形”,我们称之为第1次操作。(1)请继续在图中按以上操作对右上角的正方形进行分割,我们称之为第2次操作。(2)继续按第1次操作的方法进行第3次、第4次分割,并把分割后图中小正方形的个数填入下表:(以后每次操作都对右上角正方形进行分割)
操作次数( ) ) |
1 |
2 |
3 |
4 |
5 |
…… |
小正方形个数(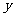 ) ) |
4 |
|
|
|
|
…… |
(3)进行第100次操作后,图中小正方形的个数是 。
 (4)能否当进行到某次操作后,使图中的小正方形
(4)能否当进行到某次操作后,使图中的小正方形
的个数为2004?若能,请求出操作的次数;
若不能,请说明理由。
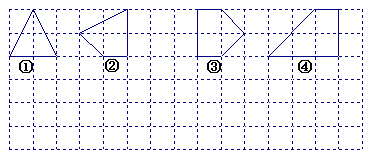 例4.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形。设格点多边形的面积为S,它各边上格点的个数和为
例4.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形。设格点多边形的面积为S,它各边上格点的个数和为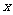 。
。
(1)上图中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出S与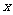 之间的关系式。
之间的关系式。
答:S= 。
|
多边形的序号 |
① |
② |
③ |
④ |
… |
|
多边形的面积S |
2 |
2.5 |
3 |
4 |
… |
各边上格点的个数和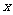 |
4 |
5 |
6 |
8 |
… |
(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有2格点。此时所画的各个多边形的面积S与它各边上格点的个数和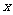 之间的关系式是:S=
。
之间的关系式是:S=
。
(3)请你继续探索,当格点多边形内部有且只有 个格点时,猜想S与
个格点时,猜想S与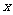 有怎样的关系?答:S=
。
有怎样的关系?答:S=
。
4. 解决问题
能从数学的角度提出问题、理解问题、并综合运用数学知识解决问题;具有一定的解决问题的基本策略;能合乎逻辑地与他人交流;具有初步的反思意识等等。
考查学生提出问题的能力时,以下几个方面的内容是应当成为考查所关注的主要对象:
能否在一些“非纯粹数学情境”--或者是生活中的与自然、社会相关的现象、或者其他学科所研究的问题情境中,识别出相关的数学对象;能否在一些数学或非数学现象中意识到有问题(疑问)存在--例如在一些图形、解析式、数据、游戏过程、自然与社会活动过程等对象中发现需要研究的数学问题;是否能够用准确的、他人可以理解的数学语言(符号)将问题清晰地表述出来等。
3. 数学思考
学生在数感与符号感、空间观念、统计意识、推理能力、应用数学解决问题的意识和方法等方面的发展情况,其内容主要包括:
能够用数来表达和交流信息;能够使用符号表达数量关系,并借助符号转换活动获得对事物的理解;能够观察到现实生活中的基本几何现象;能够运用图形形象地表达问题、借助直观进行思考与推理;能意识到做一个合理的决策需要借助统计活动去收集信息;面对数据时能对它的来源、处理方法和由此而得到的推测性结论做合理的质疑;能够正确地认识生活中的一些不确定现象。
考查“空间观念”发展情况应注意:
能否根据问题的特点和求解的需要,采用适当的方式表达一些几何对象(现象)--坐标、图形、现实模型等;是否能够在自己的头脑里进行“思想实验”--借助图形、想象、和逻辑推演从事对几何对象的各种“操作”;是否能够采用不同的方式探索研究对象的有关性质--包括观察、折叠、变换、图形的分解与组合、逻辑推演等。
2.数学活动过程
具体的评价指标:
数学活动过程中所表现出来的思维方式、思维水平,对活动对象、相关知识与方法的理解深度;从事探究、证明等活动的意识、能力和信心等。能否通过观察、实验、归纳、类比等活动获得数学猜想,并寻求证明猜想的合理性;能否使用恰当的数学语言有条理地表达自己的数学思考过程。
考查从事探索性数学活动过程的相关指标时,应注意:
能否积极有效地观察所探索的对象--通过对若干具体情况的观察而发现存在于探索对象背后的数学现象;能否采用某种明确而有效的思维方法研究这些数学现象之中的规律性--例如借助归纳、类比、逻辑判断等方法获得某种合乎情理的猜测;是否能够寻找出从逻辑的角度有效说明猜测正确的策略--知道与需要证明的猜测有实质性逻辑关系的基本数学原理,在整体上把握了一个使得猜测得以证明的“逻辑链条”;是否能够用恰当的数学语言表达自己的探索与论证过程;等等。(从知识立意、能力立意到过程立意?)
数学学业考试的考查内容以《标准》中的课程目标、“内容标准”为基本依据,不得超越。主要的考查方面包括:基础知识与基本技能;数学活动过程;数学思考;解决问题能力等。
特别地,达到《标准》所确立的数学学科毕业合格水平而必备的数学知识技能和思想方法等应当成为考查的首要内容;在此基础之上,学生在《标准》所确立的数学课程目标诸方面的进一步发展状况也应当成为考查的重要内容。
具体的考查内容--
1. 基础知识与基本技能
了解数的意义,理解数和代数运算的意义、算理,能够合理地进行基本运算与估算;能够在实际情境中有效地使用代数运算、代数模型及相关概念解决问题; 理解与操作;运算与模型
能够借助不同的方法探索几何对象的有关性质;能够使用不同的方式表达几何对象的大小、形状,和相对位置关系;能够在头脑里构建几何对象,进行几何图形的分解与组合,能对某些图形进行简单的变换;能够借助数学证明的方法确认数学命题的正确性;空间观念;探索与论证
正确理解数据的含义,能够结合实际需要有效地表达数据特征,会根据数据结果做合理的预测;了解概率的基本涵义,能够借助概率模型或通过设计具体活动解释一些事件发生的概率。统计推断;概率模型
有条件的地区还应当考查学生能否使用计算器解决相应的数值计算问题和从事有关探索规律的活动。 数值计算;探索规律
对方程(组)内容的学习情况考查,应注意:
对方程(组)作为模型的理解与掌握--是否能够在现实情境中看出相应的模型、或根据具体问题的需要列出相应的方程(组);是否掌握求解方程(组)的基本方法--包括借助估算、公式法(如果存在)或明确的求解程序得到方程(组)的(数学)解;按照要求得到有关实际问题的现实解(如果需要);领悟求解方程(组)的基本思想方法,能够在一定的程度上将其与不等式的求解方法做比较,了解其间的一致和不同;了解方程(组)与函数、不等式的联系等。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com