

2.
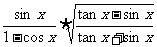
1.
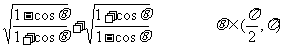
6.已知tan =3,求下列各式的值
=3,求下列各式的值

分析:思路1,可以由tan =3求出sin
=3求出sin 、cos
、cos 的值,代入求解即可;
的值,代入求解即可;
思路2,可以将要求值的表达式利用同角三角函数关系,变形为含tan 的表达式.
的表达式.
解:(1)原式分子分母同除以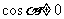 得,
得,
原式=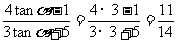
(2)原式的分子分母同除以
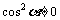 得:
得:
原式=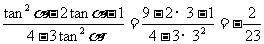
(3)用“1”的代换
原式=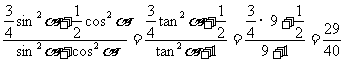
(4)原式=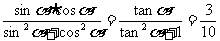
(5)  =
=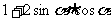 =
=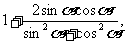
=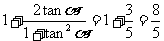
∴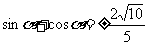
(6)同(5)
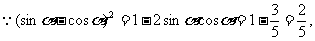
∴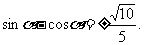
(7)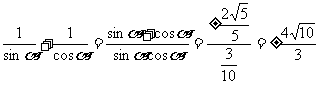

(8) =
=
=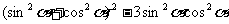
=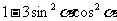 =
=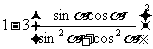
=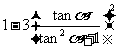 =
=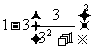 =
=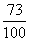
说明:数字“1”的代换,表面上看增加了运算,但同时它又可以将原表达式整体结构发生改变,给解决问题带来方面,故解题时,应给于足够的认识.
7 化简下列各式
化简下列各式
5.已知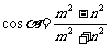 ,求tan
,求tan 和sin
和sin 的值.
的值.
分析:由已知条件可知cos 的值可能正可能负,
的值可能正可能负,
∴要分别讨论分子为正、为负的情形.
解:(1)若│m│>│n│>0
则cos >0 ∴
>0 ∴ 在Ⅰ、Ⅳ象限
在Ⅰ、Ⅳ象限
当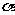 在第Ⅰ象限时
在第Ⅰ象限时


当 在第Ⅳ象限时
在第Ⅳ象限时
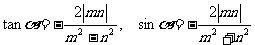

(2)若0<│m│<│n│时,则cos <0 ∴
<0 ∴ 在第II、III象限
在第II、III象限
当 在第Ⅱ象限时
在第Ⅱ象限时
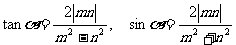

当 在第III象限时
在第III象限时


(3)若n=0、m≠0时,tan =0,sin
=0,sin =0
=0
(4) 若m=0、n≠0时,tan =0,sin
=0,sin =0
=0
说明:已知某角的一个三角函数值,求该角的其他三角函数值时要注意:
(1) 角所在的象限;
(2) 用平方关系求值时,所求三角函数的符号由角所在的象限决定;
(3)若题设中已知角的某个三角函数值是用字母给出的,则求其他函数值时,要对该字母分类讨论.
4.已知 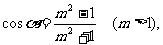 求cot
求cot 的值
的值
分析:由题意可知cos >0,∴分
>0,∴分 在Ⅰ、Ⅳ象限讨论.利用平方关系可求正弦值,利用商的关系,即可求余切值.
在Ⅰ、Ⅳ象限讨论.利用平方关系可求正弦值,利用商的关系,即可求余切值.
解:∵ m>1 ∴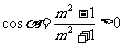 ,∴
,∴ 在第I、IV象限
在第I、IV象限
当α在第I象限时
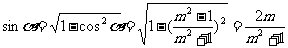
∴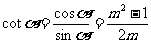
当 在第IV象限时,
在第IV象限时,
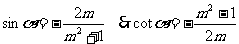
3.已知角 的终边在直线y=3x上,求sin
的终边在直线y=3x上,求sin 和cos
和cos 的值.
的值.
解:由题意可知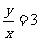
∵角 的终边在直线y=3x上
的终边在直线y=3x上
∴设P(a,3a)(a≠0)为角 终边上的任一点.
终边上的任一点.
当 在第一象限时,a>0
在第一象限时,a>0
∴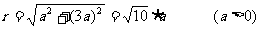
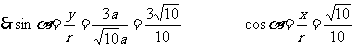
当 在第三象限,
在第三象限,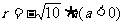
∴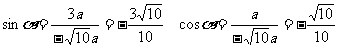
2.已知: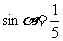 且
且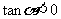 ,试用定义求
,试用定义求 的其余三个三角函数值.
的其余三个三角函数值.
分析:题目要用定义求三角函数值,则解决问题的关键应找到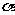 终边的所在象限.
终边的所在象限.
解:∵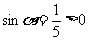 ,而
,而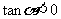
∴ 在第二象限
在第二象限
设点P(x,y)为角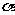 终边上任一点
终边上任一点
由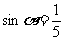 ,可设
,可设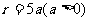 ,则
,则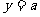 .
.
∴
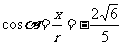 ,
,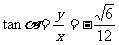 ,
,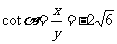 .
.
1.已知cot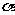 =2,求α的其余三个三角函数值.
=2,求α的其余三个三角函数值.
分析:由于cot =2>0,因此分
=2>0,因此分 在第Ⅰ、III象限时,讨论.
在第Ⅰ、III象限时,讨论.
解:∵cot =2>0 ∴α在第Ⅰ、III象限
=2>0 ∴α在第Ⅰ、III象限
当 在第Ⅰ象限时,
在第Ⅰ象限时,
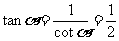 ,
,
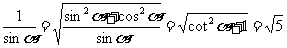
∴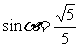 , ∴
, ∴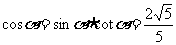
当 在第II象限时,
在第II象限时,
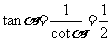
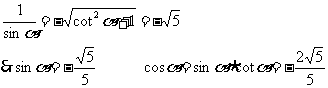
例1化简: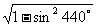
解:原式
例2 已知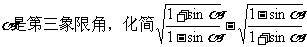
解: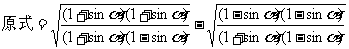
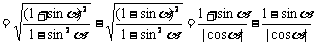
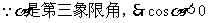
 (注意象限、符号)
(注意象限、符号)
例3求证: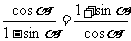
分析:思路1.把左边分子分母同乘以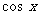 ,再利用公式变形;思路2:把左边分子、分母同乘以(1+sinx)先满足右式分子的要求;思路3:用作差法,不管分母,只需将分子转化为零;思路4:用作商法,但先要确定一边不为零;思路5:利用公分母将原式的左边和右边转化为同一种形式的结果;思路6:由乘积式转化为比例式;思路7:用综合法.
,再利用公式变形;思路2:把左边分子、分母同乘以(1+sinx)先满足右式分子的要求;思路3:用作差法,不管分母,只需将分子转化为零;思路4:用作商法,但先要确定一边不为零;思路5:利用公分母将原式的左边和右边转化为同一种形式的结果;思路6:由乘积式转化为比例式;思路7:用综合法.
证法1:左边=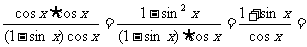 右边,
右边,
∴原等式成立
证法2:左边=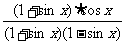 =
=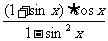
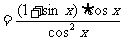 =
=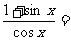 右边
右边
证法3:
∵ ,
,
∴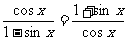

证法4:∵cosx≠0,∴1+sinx≠0,∴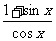 ≠0,
≠0,
∴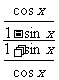 =
=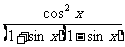 =
=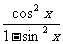 =1,
=1,
∴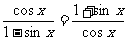 .
.
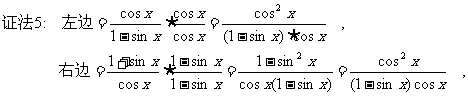 ∴左边=右边 ∴原等式成立.
∴左边=右边 ∴原等式成立.
证法6:∵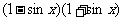 =
=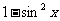 =
=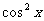 =
=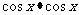
∴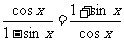 .
.
证法7:∵ , ∴
, ∴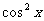 =
=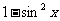
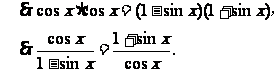
例4已知方程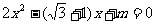 的两根分别是
的两根分别是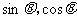 ,
,
求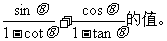
解: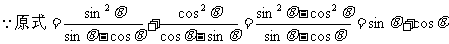
 (化弦法)
(化弦法)
例5已知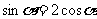 ,
,
求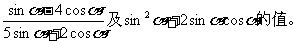
解: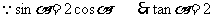
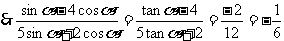
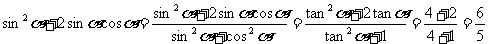 例6消去式子中的
例6消去式子中的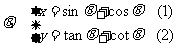
解:由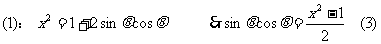
由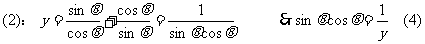
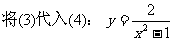 (平方消去法)
(平方消去法)
例7已知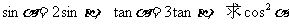
解:由题设: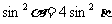 ①
①
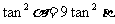 ②
②
①/②: 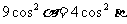 ③
③
①+③:
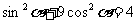

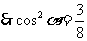
同角三角函数的基本关系公式:
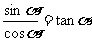
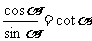
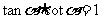
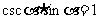
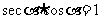


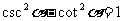
 1°“同角”的概念与角的表达形式无关,如:
1°“同角”的概念与角的表达形式无关,如:

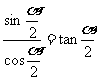
2°上述关系(公式)都必须在定义域允许的范围内成立
3°由一个角的任一三角函数值可求出这个角的其余各三角函数值,且因为利用“平方关系”公式,最终需求平方根,会出现两解,因此应尽可能少用,若使用时,要注意讨论符号
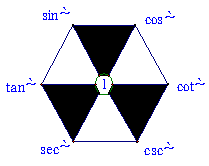
这些关系式还可以如图样加强形象记忆:
①对角线上两个函数的乘积为1(倒数关系)
②任一角的函数等于与其相邻的两个函数的积(商数关系)
③阴影部分,顶角两个函数的平方和等于底角函数的平方(平方关系)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com