11．(2009·北京市海淀区)若实数x、y满足且z＝2x+y的最小值为3，则实数b的值为________．

答案：

解析：在坐标平面内画出不等式组表示的大致平面区域，在坐标平面内平移直线2x+y＝0，注意到当直线平移到经过直线2x－y＝0与y＝－x+b的交点时，目标函数z＝2x+y取得最小值，再结合z＝2x+y的最小值为3，分析确定b＝.

10．(2008·襄樊质检)动点P(a，b)在不等式组

表示的平面区域内部及边界上运动，则ω＝的取值范围是________．

答案： (－∞ ，－2]∪[2，+∞)

解析：

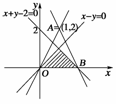
画出可行域如上图，ω=的意义为可行域上的点P(a，b)与定点A(1,2)连线的斜率，k_AB=-2，k_AO=2，则ω=的取值范围是(-∞，-2]∪[2，+∞)，故填(-∞ ，-2]∪[2，+∞)．

9．设D是不等式组表示的平面区域，则D中的点P(x，y)到直线x+y＝10距离的最大值是__________．

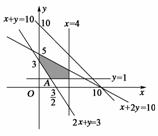
答案：4

分析：考查线性规划的应用．

解析：画出可行域，由图知最优解为A(1,1)，故A到x+y＝10的距离为＝4.故填4.

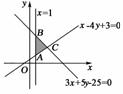
8．如果实数x、y满足目标函数z＝kx+y的最大值为12，最小值为3，那么实数k的值为(　)

A．2　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．－2

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D．不存在

答案：A

解析：直线x=1与x-4y+3=0、3x+5y-25=0的交点分别是A(1,1)，B(1，)，直线x-4y+3=0与3x+5y-25=0的交点是C(5,2)，z=kx+y变形为z-kx-y=0.结合图形分析知，当-k<-时，由题意得由此解得k=2；当k≤时，结合图形分析可知，显然不存在满足题意的k值．故选A.

7．在平面直角坐标系 xOy中，已知平面区域A＝，则平面区域B＝的面积为(　)

A．2　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．1

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

答案：B

分析：考查线性规划的基础知识．

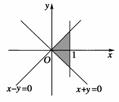
解析：令

得

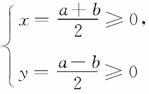
得

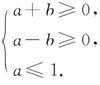画出平面区域B的可行域如上图，得到面积为1.

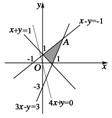
6．设变量x，y满足约束条件

则目标函数z＝4x+y的最大值为(　)

A．4　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．11

C．12　 　　　　　　　　　　　　　　　　　　　　　　　　 D．14

答案：B

分析：考查运用线性规划解决问题的能力．

解析：画出可行域如右图，由图可知目标函数最优解为A(2,3)

y_max＝4×2+3＝11，故选B.

5．若不等式组表示的平面区域是一个三角形，则a的取值范围是(　)

A．a≥　 　　　　　　　　　　　　　　　　　　　　　　　 B．0<a≤1

C．1≤a≤　 　　　　　　　　　　　　　　　　　　　　 D．0<a≤1或a≥

答案：D

分析：考查线性约束条件及直线截距的几何意义．着重考查数形结合思想．

解析：由图形知，要使平面区域为三角形，只需动直线l：x+y=a在l₁、l₂之间或l₃上方．故选D.

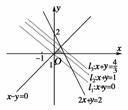
4．下面给出的四个点中，到直线x－y+1＝0的距离为，且位于表示的平面区域内的点是(　)

A．(1,1)　　　　　　　　　　　　　　 B．(－1,1)

C．(－1，－1)　 　　　　　　　　　　　　　　　　　　 D．(1，－1)

答案：C

分析：考查点到直线的距离公式，线性约束条件．

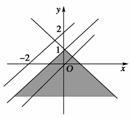
解法一：把(1,1)代入x+y-1<0不成立，排除A；

把(-1,1)代入x-y-1>0不成立，排除B；

而(1，-1)到直线x-y+1=0的距离为，排除D.故选C.

解法二：到直线x-y+1=0的距离为的点的轨迹为两条直线x-y=0，x-y+2=0.

又由

由图形得，故选C.

3．(2008·天津)设变量x，y满足约束条件

则目标函数z＝5x+y的最大值为(　)

A．2　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．3

C．4　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．5

答案：D

解析：先画出可行域，如下图：

最优解为A(1,0)．

∴z_max=5，故选D.

2．(2008·北京)若实数x，y满足则z＝3^x+2y的最小值是(　)

A．0　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．1

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．9

答案：B

解析：此题考查线性规划的知识，比较容易．

当x＝0，y＝0时，(x+2y)_min＝0，

此时z_min＝3⁰＝1，故选B.