5．一个做匀加速直线运动的物体，初速度v₀＝2.0 m/s，它在第3 s内通过的位移是4.5 m，则它的加速度为(　)

A．0.5 m/s² 　　　　　　　B．1.0 m/s²

C．1.5 m/s²　 　　　　　　D．2.0 m/s²

[解析]　物体在第3 s内的平均速度 ₃＝4.5 m/s，即为第3 s的中间时刻t＝2.5 s时的瞬时速度．

又v＝v₀+at

得：a＝＝ m/s²＝1.0 m/s².

[答案]　B

4．做匀加速直线运动的质点，运动了t s，下列说法中正确的是(　)

A．它的初速度越大，通过的位移一定越大

B．它的加速度越大，通过的位移一定越大

C．它的末速度越大，通过的位移一定越大

D．它的平均速度越大，通过的位移一定越大

[解析]　由匀加速直线运动的位移公式x＝v₀t+at²知，在时间t一定的情况下，只有初速v₀和加速度a都较大时，位移x才较大，只有v₀或a一个量较大，x不一定大，所以A、B不正确；由匀加速直线运动的位移公式x＝t知，在时间t一定的情况下，只有初速v₀和末速v_t都较大时，位移x才较大，只有v_t一个量较大，x不一定大，所以C不正确；由位移公式x＝t知，在时间t一定的情况下，平均速度 较大，位移x一定较大，所以D正确．

[答案]　D

3．从静止开始做匀加速直线运动的物体，0-10 s内的位移是10 m，那么在10 s-20 s内的位移是(　)

A．20 m　 　　　　　　　　B．30 m

C．40 m　 　　　　　　　　D．60 m

[解析]　当t＝10 s时，Δx＝a(2t)²－at²＝at²＝at²·3＝10×3 m＝30 m.

[答案]　B

2．某质点的位移随时间变化规律的关系是x＝4t+2t²，x与t的单位分别为m和s，则质点的初速度与加速度分别为(　)

A．4 m/s与2 m/s²　 　　　　　　　B．0与4 m/s²

C．4 m/s与4 m/s² 　　　　　　　　D．4 m/s与0

[解析]　匀变速直线运动的位移与时间关系式为x＝v₀t+at²，对比x＝4t+2t²，得出v₀＝4 m/s，a＝4 m/s²，C正确．

[答案]　C

1．汽车由静止开始做匀加速直线运动，速度达到v时立即做匀减速直线运动，最后停止，运动的全部时间为t，则汽车通过的全部位移为(　)

A.vt　 　　　　　　　　　　B.vt

C.vt 　　　　　　　　　　D.vt

[解析]　匀变速直线运动中一段时间内的平均速度等于该段时间初、末速度的平均值，由题意知，汽车在加速和减速两过程的平均速度均为，故全程的位移x＝vt，B项正确．

[答案]　B

6.匀变速直线运动位移与时间的关系

(本栏目内容，在学生用书中以活页形式分册装订！)

15．配制两种药剂，需要甲、乙两种原料，已知配A种药需要甲料3 mg，乙料5 mg；配B种药需要甲料5 mg，乙料4 mg.今有甲料20 mg，乙料25 mg，若A，B两种药至少各配一剂，问最多能各配几剂？

解：设A，B两种药分别能配x，y剂，x，y∈N^*，则有不等式组

⇒

符合条件的解集是以直线x＝1，y＝1，y＝－+4，y＝－x+为边界所围成的区域(即图中的阴影部分)，这个区域内的整数点有(1,1)，(1,2)，(1,3)，(2,1)，(3,1)，(3,2)，(4,1)．

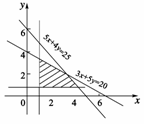
所以，在保证A，B两种药至少各配一剂的条件下，A种药最多配4剂，B种药最多配3剂．

14．在R上可导的函数f(x)＝x³+ax²+2bx+c，当x∈(0,1)时取得极大值，当x∈(1,2)时取得极小值，求点(a，b)对应的区域的面积以及的取值范围．

解：函数f(x)的导数为f′(x)＝x²+ax+2b，当x∈(0,1)时，f(x)取得极大值，当x∈(1,2)时，f(x)取得极小值，则方程x²+ax+2b＝0有两个根，一个根在区间(0,1)内，另一个根在区间(1,2)内，由二次函数f′(x)＝x²+ax+2b的图象与方程x²+ax+2b＝0根的分布之间的关系可以得到⇒，

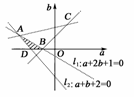
在aOb平面内作出满足约束条件的点(a，b)对应的区域为△ABD(不包括边界)，如右图阴影部分，其中点A(-3,1)，B(-1,0)，D(-2,0)．

△ABD的面积为S_△ABD=|BD|×h= (h为点A到a轴的距离)．

点C(1,2)与点(a，b)连线的斜率为，

显然∈(k_CA，k_CB)，

即∈(,1)．

13．两种大小不同的钢板可按下表截成A，B，C三种规格成品：

	A规格	B规格	C规格
第一种钢板	2	1	1
第二种钢板	1	2	3

某建筑工地需A，B，C三种规格的成品分别为15,18,27块，问怎样截这两种钢板，可得所需三种规格成品，且所用钢板张数最小．

解：设需要第一种钢板x张，第二种钢板y张，钢板总数为z张，z＝x+y，

约束条件为：

作出可行域如下图所示：

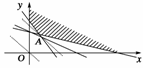
令z=0，作出基准直线l：y=-x，平行移动直线l发现在可行域内，经过直线x+3y=27和直线2x+y=15的交点A(，)可使z取最小，由于，都不是整数，而最优解(x，y)中，x，y必须都是整数，可行域内点A(，)不是最优解；

通过在可行域内画网格发现，经过可行域内的整点且与A(，)点距离最近的直线是x+y=12，经过的整点是B(3,9)和C(4,8)，它们都是最优解．

答：要截得所需三种规格的钢板，且使所截两种钢板的张数最少的方法有两种：

第一种截法是截第一种钢板3张，第二种钢板9张；

第二种截法是截第一种钢板4张，第二种钢板8张；

两种方法都最少要截两种钢板共12张。

12．已知变量x，y满足的约束条件为.若目标函数z＝ax+y(其中a>0)仅在点(3,0)处取得最大值，求a的取值范围．

解：

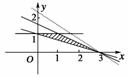
依据约束条件，画出可行域．∵直线x+2y-3=0的斜率k₁=-，目标函数z=ax+y(a>0)对应直线的斜率k₂=-a，若符合题意，则须k₁>k₂，即->-a，得a>.