
3.下列句子中标点符号使用正确的一句是
A.作为音乐教师的她,轻轻地哼着“摇篮曲”,孩子在她怀中慢慢睡着了。
B.有的人可能终生是个谜,但只要他是英雄,不管谜面如何,谜底决然是个“公”字。
C.他暗自下定决心:不看电视,不听音乐,经过两个月的奋战,终于译完了这本书。
D.“但愿人长久,千里共婵娟。”的诗句,出自宋代诗人苏轼的《水调歌头明月几时有》一词。
2.下列句子中标点符号使用正确的一句是
A.如果你同意,二、三十棵树可以成为林,那么这里要说的,正是这样一个桃林。
B.我父、母都是美国留学生,母亲先学医,后又攻读工艺美术。
C.他受到领导信任,单独掌管一个国家重点建设项目、大发电厂的拨款计划。
D.眼、耳、鼻、舌、身是人体的五个官能。
1.依次填入下面一段话中画线处的标点,恰当的一组是
“画人画鬼高人一等,刺贪刺虐入骨三分” ① 这是郭沫若为蒲松龄纪念馆聊斋堂写的对联。“画人画鬼”,指《聊斋志异》的题材内容 ② 它借狐鬼故事来达到“刺贪刺虐”的目的;“高人一等”,是评价蒲松龄在文学史上的贡献;“入骨三分”,则概括了他在创作上的成就。今天这节课要学习他的名篇 ③ 促织,让我们来看看这个评价是否恰当 ④
|
|
① |
② |
③ |
④ |
|
A |
, |
, |
《
》 |
。 |
|
B |
。 |
; |
“
” |
。 |
|
C |
。 |
; |
《
》 |
? |
|
D |
。 |
, |
“
” |
? |
(16)(本小题满分12分)在 ABC中,C-A=
ABC中,C-A=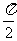 , sinB=
, sinB=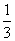 。
。
(I)求sinA的值;
(II)设AC=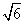 ,求
,求 ABC的面积。
ABC的面积。
(16)本小题主要考查三角恒等变换、正弦定理、解三角形等有关知识,考查运算求解能力。本小题满分12分
解:(I)由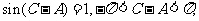 知
知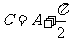 。
。
又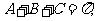 所以
所以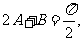 即
即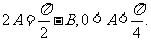
故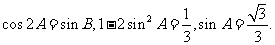
(II)由(I)得: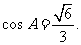
又由正弦定理,得: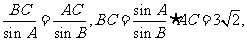
所以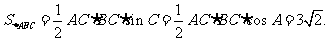
(17)(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区。B肯定是受A感染的。对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是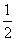 。同样也假定D受A、B和C感染的概率都是
。同样也假定D受A、B和C感染的概率都是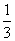 。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
(17)本小题主要考查古典概型及其概率计算,考查取有限个值的离散型随机变量及其分布列和均值的概念,通过设置密切贴近现实生活的情境,考查概率思想的应用意识和创新意识。体现数学的科学价值。本小题满分12分。
|
X |
1 |
2 |
3 |
|
P |
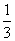 |
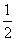 |
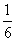 |
解:随机变量X的分布列是
X的均值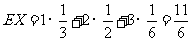 。
。
附:X的分布列的一种求法
共有如下6种不同的可能情形,每种情形发生的概率都是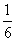 :
:
|
① |
② |
③ |
④ |
⑤ |
⑥ |
|
A-B-C-D |
A-B-C └D |
A-B-C └D |
A-B-D └C |
A-C-D └B |
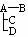 |
在情形①和②之下,A直接感染了一个人;在情形③、④、⑤之下,A直接感染了两个人;在情形⑥之下,A直接感染了三个人。
 (18)(本小题满分13分)
(18)(本小题满分13分)
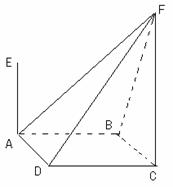
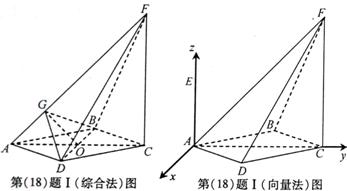
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,
BD=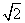 ,AE、CF都与平面ABCD垂直,AE=1,CF=2。
,AE、CF都与平面ABCD垂直,AE=1,CF=2。
(I)求二面角B-AF-D的大小;
(II)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积。
(18) 本小题主要考查直线与直线、直线与平面、平面与平面的位置关系、相交平面所成二面角以及空间几何体的体积计算等知识,考查空间想象能力和推理论证能力、利用综合法或向量法解决立体几何问题的能力。本小题满分13分。
解:(I)(综合法)连接AC、BD交于菱形的中心O,过O作OG⊥AF,G为垂足。连接BG、DG。
由BD⊥AC,BD⊥CF,得:BD⊥平面ACF,故BD⊥AF.
于是AF⊥平面BGD,所以BG⊥AF,DG⊥AF,∠BGD为二面角B-AF-D的平面角。
由FC⊥AC,FC=AC=2,得∠FAC=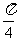 ,OG=
,OG=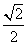 .
.
由OB⊥OG,OB=OD=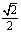 ,得∠BGD=2∠BGO=
,得∠BGD=2∠BGO=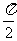 .
.
(向量法)以A为坐标原点,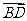 、
、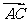 、
、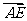 方向分别为
方向分别为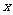 轴、
轴、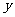 轴、
轴、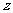 轴的正方向建立空间直角坐标系(如图).于是
轴的正方向建立空间直角坐标系(如图).于是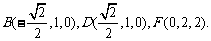
设平面ABF的法向量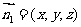 ,则由
,则由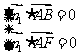 得
得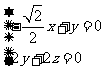 。
。
令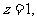 得
得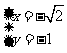 ,
,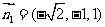
同理,可求得平面ADF的法向量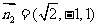 。
。
由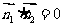 知,平面ABF与平面ADF垂直,
知,平面ABF与平面ADF垂直,
二面角B-AF-D的大小等于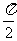 。
。
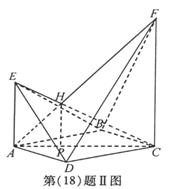
(II)连EB、EC、ED,设直线AF与直线CE相交于点H,则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD。
过H作HP⊥平面ABCD,P为垂足。
因为EA⊥平面ABCD,FC⊥平面ABCD,,所以平面ACFE⊥平面ABCD,从而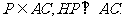
由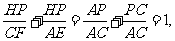 得
得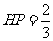 。
。
又因为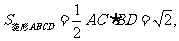
故四棱锥H-ABCD的体积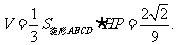
(19)(本小题满分12分)
已知函数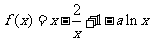 ,a>0,讨论
,a>0,讨论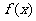 的单调性.
的单调性.
(19)本小题主要考查函数的定义域、利用导数等知识研究函数的单调性,考查分类讨论的思想方法和运算求解的能力。本小题满分12分。
解: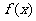 的定义域是(0,+
的定义域是(0,+ ),
),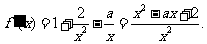
设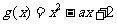 ,二次方程
,二次方程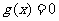 的判别式
的判别式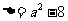 .
.
① 当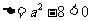 ,即
,即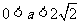 时,对一切
时,对一切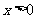 都有
都有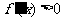 ,此时
,此时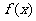 在
在 上是增函数。
上是增函数。
② 当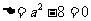 ,即
,即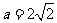 时,仅对
时,仅对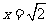 有
有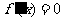 ,对其余的
,对其余的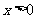 都有
都有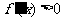 ,此时
,此时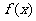 在
在 上也是增函数。
上也是增函数。
③ 当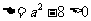 ,即
,即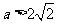 时,
时,
方程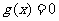 有两个不同的实根
有两个不同的实根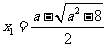 ,
,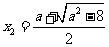 ,
,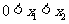 .
.
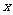 |
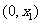 |
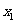 |
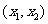 |
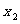 |
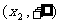 |
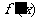 |
+ |
0 |
_ |
0 |
+ |
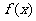 |
单调递增 |
极大 |
单调递减 |
极小 |
单调递增 |
此时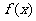 在
在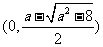 上单调递增, 在
上单调递增, 在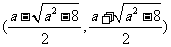 是上单调递减, 在
是上单调递减, 在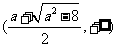 上单调递增.
上单调递增.
(20)(本小题满分13分)
点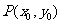 在椭圆
在椭圆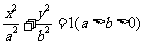 上,
上,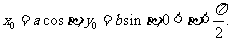 直线
直线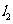 与直线
与直线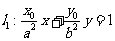 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为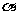 ,直线
,直线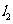 的倾斜角为
的倾斜角为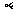 .
.
(I)证明: 点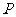 是椭圆
是椭圆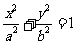 与直线
与直线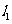 的唯一交点;
的唯一交点;
(II)证明: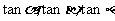 构成等比数列。
构成等比数列。
(20)本小题主要考查直线和椭圆的标准方程和参数方程,直线和曲线的几何性质,等比数列等基础知识。考查综合运用知识分析问题、解决问题的能力。本小题满分13分。
解:(I)(方法一)由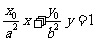 得
得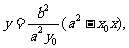 代入椭圆
代入椭圆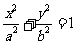 ,
,
得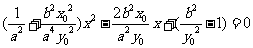 .
.
将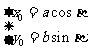 代入上式,得
代入上式,得 从而
从而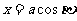
因此,方程组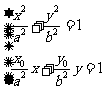 有唯一解
有唯一解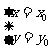 ,即直线
,即直线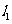 与椭圆有唯一交点P.
与椭圆有唯一交点P.
(方法二)显然P是椭圆与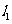 的交点,若Q
的交点,若Q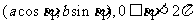 是椭圆与
是椭圆与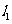 的交点,代入
的交点,代入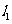 的方程
的方程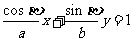 ,得
,得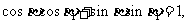
即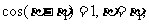 故P与Q重合。
故P与Q重合。
(方法三)在第一象限内,由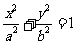 可得
可得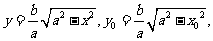
椭圆在点P处的切线斜率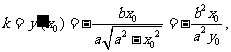
切线方程为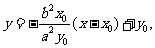 即
即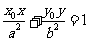 。
。
因此,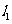 就是椭圆在点P处的切线。
就是椭圆在点P处的切线。
根据椭圆切线的性质,P是椭圆与直线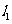 的唯一交点。
的唯一交点。
(II)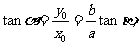
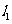 的斜率为
的斜率为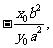
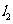 的斜率为
的斜率为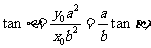
由此得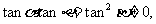
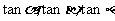 构成等比数列。
构成等比数列。
(21)(本小题满分13分)
首项为正数的数列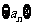 满足
满足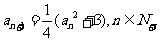
(I)证明:若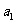 为奇数,则对一切
为奇数,则对一切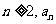 都是奇数;
都是奇数;
(II)若对一切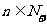 都有
都有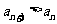 ,求
,求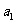 的取值范围。
的取值范围。
(21)本小题主要考查数列、数学归纳法和不等式的有关知识,考查推理论证、抽象概括、运算求解和探究能力,考查学生是否具有审慎思维的习惯和一定的数学视野。本小题满分13分。
解:(I)已知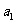 是奇数,假设
是奇数,假设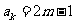 是奇数,其中
是奇数,其中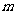 为正整数,
为正整数,
则由递推关系得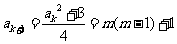 是奇数。
是奇数。
根据数学归纳法,对任何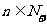 ,
,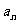 都是奇数。
都是奇数。
(II)(方法一)由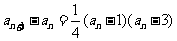 知,
知,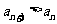 当且仅当
当且仅当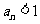 或
或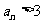 。
。
另一方面,若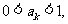 则
则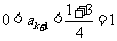 ;若
;若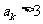 ,则
,则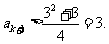
根据数学归纳法,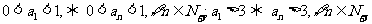
综合所述,对一切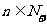 都有
都有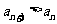 的充要条件是
的充要条件是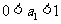 或
或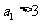 。
。
(方法二)由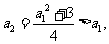 得
得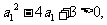 于是
于是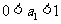 或
或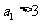 。
。
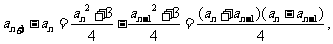
因为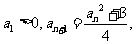 所以所有的
所以所有的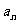 均大于0,因此
均大于0,因此 与
与 同号。
同号。
根据数学归纳法,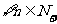 ,
, 与
与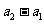 同号。
同号。
因此,对一切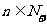 都有
都有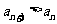 的充要条件是
的充要条件是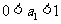 或
或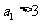 。
。
(11)若随机变量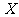 -
-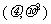 ,则
,则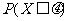 =________.
=________.
解答: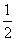
 (12)以直角坐标系的原点为极点,
(12)以直角坐标系的原点为极点,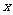 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位。已知直线的极坐标方程为
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位。已知直线的极坐标方程为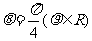 ,它与曲线
,它与曲线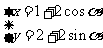 (
(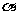 为参数)相交于两点A和B,则|AB|=_______.
为参数)相交于两点A和B,则|AB|=_______.
解答: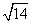
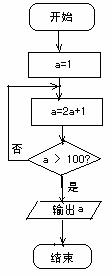
(13) 程序框图(即算法流程图)如图所示,其输出结果是_______.
解答:127
(14)给定两个长度为1的平面向量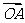 和
和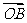 ,它们的夹角为
,它们的夹角为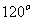 .如图所示,点C在以O为圆心的圆弧AB上变动.若
.如图所示,点C在以O为圆心的圆弧AB上变动.若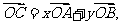 其中
其中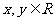 ,则
,则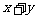 的最大值是=________.
的最大值是=________.
解答: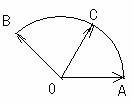 2
2
(15)对于四面体ABCD,下列命题正确的是_________
(写出所有正确命题的编号)。
1相对棱AB与CD所在的直线是异面直线;
2由顶点A作四面体的高,其垂足是 BCD的三条高线的交点;
BCD的三条高线的交点;
3若分别作 ABC和
ABC和 ABD的边AB上的高,则这两条高所在直线异面;
ABD的边AB上的高,则这两条高所在直线异面;
4分别作三组相对棱中点的连线,所得的三条线段相交于一点;
5最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱。
解答:145
(1)i是虚数单位,若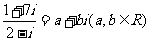 ,则乘积
,则乘积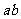 的值是(B)
的值是(B)
(A)-15 (B)-3 (C)3 (D)15
(2)若集合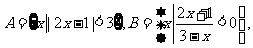 则A∩B是(D)
则A∩B是(D)
(A) 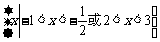 (B)
(B) 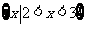
(C) 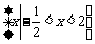 (D)
(D) 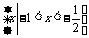
(3)下列曲线中离心率为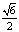 的是(B)
的是(B)
(A)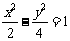 (B)
(B)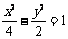 (C)
(C)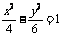 (D)
(D)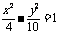
(4)下列选项中,p是q的必要不充分条件的是(A)
(A)p: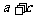 >b+d , q:
>b+d , q: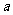 >b且c>d
>b且c>d
(B)p:a>1,b>1 q: 的图像不过第二象限
的图像不过第二象限
(C)p: x=1,
q: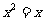
(D)p:a>1,
q: 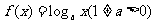 在
在 上为增函数
上为增函数
(5)已知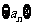 为等差数列,
为等差数列,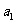 +
+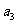 +
+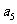 =105,
=105,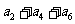 =99,以
=99,以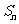 表示
表示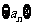 的前
的前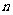 项和,则使得
项和,则使得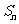 达到最大值的
达到最大值的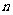 是(B)
是(B)
(A)21 (B)20 (C)19 (D) 18
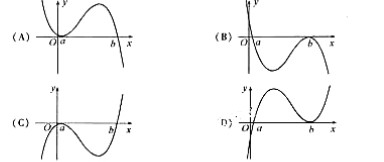
(6)设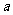 <b,函数
<b,函数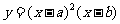 的图像可能是(C)
的图像可能是(C)
(7)若不等式组 所表示的平面区域被直线
所表示的平面区域被直线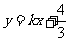 分为面积相等的两部分,则
分为面积相等的两部分,则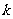 的值是(A) (A)
的值是(A) (A)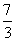 (B)
(B)
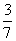 (C)
(C)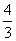 (D)
(D) 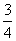
(8)已知函数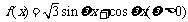 ,
,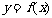 的图像与直线
的图像与直线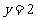 的两个相邻交点的距离等于
的两个相邻交点的距离等于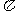 ,则
,则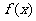 的单调区间是(C)
的单调区间是(C)
(A)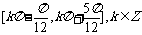 (B)
(B)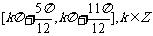
(C)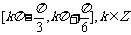 (D)
(D)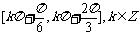
(9)已知函数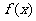 在R上满足
在R上满足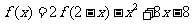 ,则曲线
,则曲线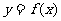 在点
在点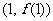 处的切线方程是(A)
处的切线方程是(A)
(A)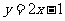 (B)
(B)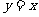 (C)
(C)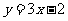 (D)
(D)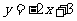
(10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于(D)
(A)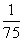 (B)
(B) 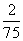 (C)
(C)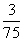 (D)
(D)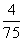
2、丧夫之痛,悼亡之情;寡居的孤独、凄苦;家国之痛,故土之思。
六、拓展
1、中心句:这次第,怎一个愁字了得?
2、李清照的“愁”有哪些意思?仅仅只是“悼亡”吗?
--明确:
1、中心句?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com