

2.给下面一段话中加点的字注音。(2分)
我憧( )憬着美好的明天,我向往着幸福的未来。但我知道:美好明天与幸福未来的实现,需要锲( )而不舍的拼搏,需要迎难而上的执着。
1.下面句子中有两个错别字,请改正后用正楷字将整个句子抄写在田字格中。(2分)
五彩缤分的花季,朝气篷勃的青春。
23. (本题满分10分)
对于正整数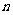 ≥2,用
≥2,用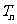 表示关于
表示关于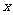 的一元二次方程
的一元二次方程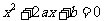 有实数根的有序数组
有实数根的有序数组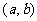 的组数,其中
的组数,其中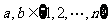 (
(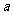 和
和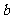 可以相等);对于随机选取的
可以相等);对于随机选取的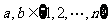 (
(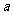 和
和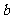 可以相等),记
可以相等),记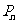 为关于
为关于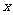 的一元二次方程
的一元二次方程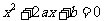 有实数根的概率。
有实数根的概率。
(1)求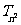 和
和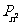 ;
;
(2)求证:对任意正整数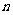 ≥2,有
≥2,有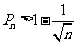 .
.
[解析] [必做题]本小题主要考查概率的基本知识和记数原理,考查探究能力。满分10分。

海南宁夏卷
(22)(本小题满分10分)选修4-1;几何证明选讲
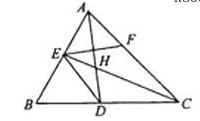 如图,已知
如图,已知 ABC中的两条角平分线
ABC中的两条角平分线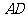 和
和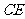 相交于
相交于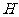 ,
, B=60
B=60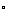 ,
,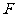 在
在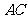 上,且
上,且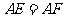 。
。 

(1)证明: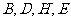 四点共圆;
四点共圆;
(2)证明:CE平分 DEF。
DEF。
(22)解:
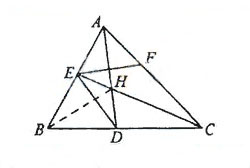 (Ⅰ)在△ABC中,因为∠B=60°,
(Ⅰ)在△ABC中,因为∠B=60°, 

所以∠BAC+∠BCA=120°.
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°, 

故∠AHC=120°.
于是∠EHD=∠AHC=120°.
因为∠EBD+∠EHD=180°,
所以B,D,H,E四点共圆。
(Ⅱ)连结BH,则BH为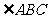 的平分线,得
的平分线,得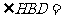 30°
30° 

由(Ⅰ)知B,D,H,E四点共圆, 

所以 30°
30°
又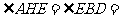 60°,由已知可得
60°,由已知可得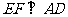 ,
,
可得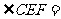 30°
30° 

所以CE平分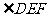
(23)(本小题满分10分)选修4-4:坐标系与参数方程。
已知曲线C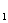 :
: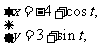 (t为参数), C
(t为参数), C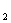 :
: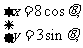 (
(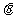 为参数)。
为参数)。
(1)化C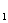 ,C
,C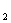 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C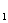 上的点P对应的参数为
上的点P对应的参数为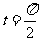 ,Q为C
,Q为C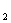 上的动点,求
上的动点,求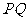 中点
中点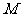 到直线
到直线
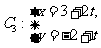 (t为参数)距离的最小值。
(t为参数)距离的最小值。 

(23)解:
(Ⅰ)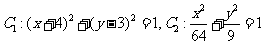


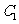 为圆心是
为圆心是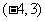 ,半径是1的圆。
,半径是1的圆。
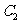 为中心是坐标原点,焦点在
为中心是坐标原点,焦点在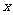 轴上,长半轴长是8,短半轴长是3的椭圆。
轴上,长半轴长是8,短半轴长是3的椭圆。 

(Ⅱ)当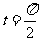 时,
时,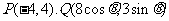 ,故
,故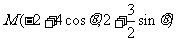
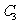 为直线
为直线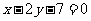 ,
,
M到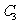 的距离
的距离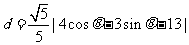


从而当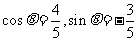 时,
时,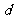 取得最小值
取得最小值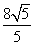


(24)(本小题满分10分)选修4-5:不等式选讲
如图,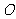 为数轴的原点,
为数轴的原点,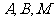 为数轴上三点,
为数轴上三点,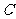 为线段
为线段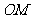 上的动点,设
上的动点,设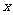 表示
表示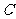 与原点的距离,
与原点的距离,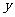 表示
表示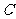 到
到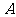 距离4倍与
距离4倍与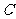 到
到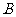 距离的6倍的和.
距离的6倍的和.
(1)将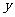 表示为
表示为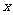 的函数;
的函数;
(2)要使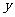 的值不超过70,
的值不超过70,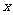 应该在什么范围内取值?
应该在什么范围内取值?
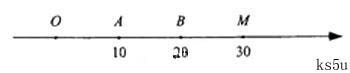


(24)解:
(Ⅰ)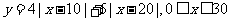


(Ⅱ)依题意,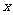 满足
满足
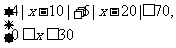
解不等式组,其解集为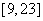
所以 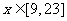
辽宁理卷
( 22 ) (本小题满分 10 分)选修 4- l :几何证明选讲
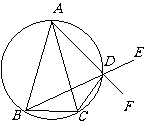 己知△ABC中,AB=AC , D是△ABC外接圆
己知△ABC中,AB=AC , D是△ABC外接圆
劣弧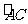 上的点(不与点A , C重合),延长BD至E。
上的点(不与点A , C重合),延长BD至E。
(1)求证:AD 的延长线平分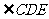 ;
;
(2)若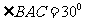 ,△ABC中BC边上的高
,△ABC中BC边上的高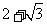 ,
,
求△ABC外接圆的面积.
( 22 ) 解:( 1 )如图,设F为AD延长线上一点,∵A,B,C, D 四点共圆,
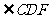 =
=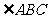 , 又AB=AC ,∴
, 又AB=AC ,∴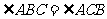 ,且
,且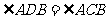 ,
,
∴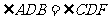 ,对顶角
,对顶角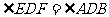 ,故
,故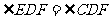 ,
,
 故AD 的延长线平分
故AD 的延长线平分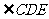 。---------------5分
。---------------5分
.( 2)设O为外接圆圆心,连接AO交BC于H ,则AH⊥BC ,
连接 OC ,由题意 OAC=
OAC= OCA =
OCA =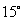 ,
,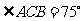 ,
,
∴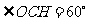 ,设圆半径为r,则
,设圆半径为r,则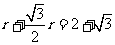 ,
,
得:r= 2 ,故外接圆面积为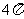 。 ---------10 分
。 ---------10 分
( 23 ) (本小题满分 10 分)选修 4- 4 :极坐标与参数方程
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为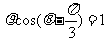 ,M , N分别为曲线C与x轴,y轴的交点.
,M , N分别为曲线C与x轴,y轴的交点.
(1)写出曲线C的直角坐标方程,并求M , N的极坐标;
(2)设M , N的中点为P,求直线OP的极坐标方程.
(
23 )解:(1)由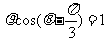 得:
得: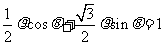 ,
,
∴曲线C的直角坐标方程为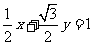 ,即
,即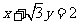 ,
,
当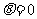 时,
时, ,∴M的极坐标(2,0);
,∴M的极坐标(2,0);
当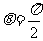 时,
时,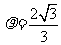 ,∴N的极坐标
,∴N的极坐标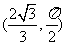 。-----------------5分
。-----------------5分
(2)M的直角坐标为(2,0),N的直角坐标为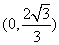 ,∴P的直角坐标为
,∴P的直角坐标为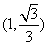 ,
,
则P的极坐标为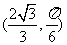 ,直线OP的极坐标方程为
,直线OP的极坐标方程为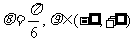 .----10分
.----10分
( 24 ) (本小题满分 10 分)选修 4- 5 :不等式选讲
设函数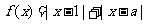 ,
,
(1)若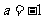 ,解不等式
,解不等式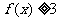 ;
;
(2)如果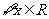 ,
,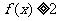 ,求a的取值范围。
,求a的取值范围。
(
24 )解:(1)当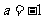 时,
时,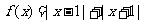 ,由
,由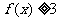 得:
得: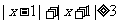 ,
,
(法一)由绝对值的几何意义知不等式的解集为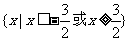 。
。
(法二)不等式可化为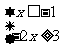 或
或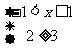 或
或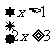 ,
,
∴不等式的解集为 。-------------5分
。-------------5分
(2)若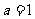 ,
, ,不满足题设条件;
,不满足题设条件;
若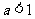 ,
,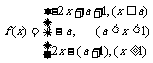 ,
,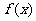 的最小值为
的最小值为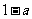 ;
;
若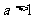 ,
,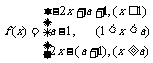 ,
,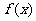 的最小值为
的最小值为 。
。
所以对于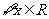 ,
,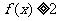 的充要条件是
的充要条件是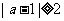 ,从而a的取值范围
,从而a的取值范围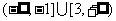 。-------------10分
。-------------10分
22. (本题满分10分)
(本题满分10分)
在平面直角坐标系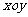 中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在
中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在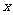 轴上。
轴上。
(1)求抛物线C的标准方程;
(2)求过点F,且与直线OA垂直的直线的方程;
(3)设过点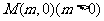 的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为
的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为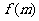 ,求
,求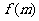 关于
关于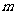 的表达式。
的表达式。
[解析] [必做题]本小题主要考查直线、抛物线及两点间的距离公式等基本知识,考查运算求解能力。满分10分。


21.[选做题]在A、B、C、D四小题中只能选做两题,每小题10分,共计20分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
 A.选修4 - 1:几何证明选讲
A.选修4 - 1:几何证明选讲
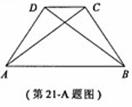
如图,在四边形ABCD中,△ABC≌△BAD.
求证:AB∥CD.
[解析] 本小题主要考查四边形、全等三角形的有关知识,考查推理论证能力。满分10分。
证明:由△ABC≌△BAD得∠ACB=∠BDA,故A、B、C、D四点共圆,从而∠CBA=∠CDB。再由△ABC≌△BAD得∠CAB=∠DBA。因此∠DBA=∠CDB,所以AB∥CD。
B. 选修4 - 2:矩阵与变换
求矩阵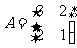 的逆矩阵.
的逆矩阵.
[解析] 本小题主要考查逆矩阵的求法,考查运算求解能力。满分10分。
解:设矩阵A的逆矩阵为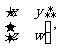 则
则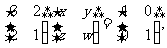
即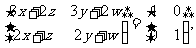 故
故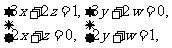
解得: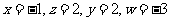 ,
,
从而A的逆矩阵为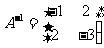 .
.
C. 选修4 - 4:坐标系与参数方程
已知曲线C的参数方程为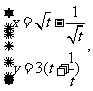 (
(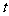 为参数,
为参数,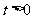 ).
).
求曲线C的普通方程。
[解析] 本小题主要考查参数方程和普通方程的基本知识,考查转化问题的能力。满分10分。
解:因为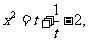 所以
所以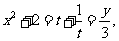
故曲线C的普通方程为: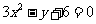 .
.
D. 选修4 - 5:不等式选讲
设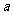 ≥
≥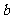 >0,求证:
>0,求证: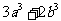 ≥
≥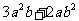 .
.
[解析] 本小题主要考查比较法证明不等式的常见方法,考查代数式的变形能力。满分10分。
证明:
因为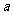 ≥
≥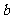 >0,所以
>0,所以 ≥0,
≥0,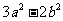 >0,从而
>0,从而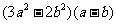 ≥0,
≥0,
即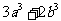 ≥
≥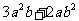 .
.
[必做题]第22题、第23题,每题10分,共计20分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
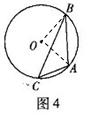
15.(几何证明选讲选做题)如图4,点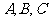 是圆
是圆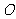 上的点, 且
上的点, 且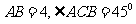 , 则圆
, 则圆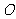 的面积等于 .
的面积等于 .
[解析]解法一:连结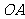 、
、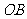 ,则
,则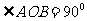 ,∵
,∵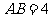 ,
,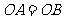 ,∴
,∴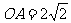 ,则
,则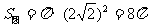 ;解法二:
;解法二: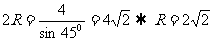 ,则
,则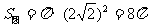 .
.
江苏卷
14.(不等式选讲选做题)不等式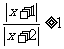 的实数解为
.
的实数解为
.
 [解析]
[解析]
 且
且 .
.
13.(坐标系与参数方程选做题)若直线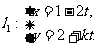 (
(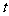 为参数)与直线
为参数)与直线 (
(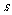 为参数)垂直,则
为参数)垂直,则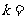 .
.
[解析]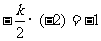 ,得
,得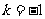 .
.
27.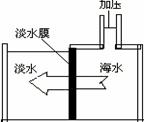 海水淡化可以采用膜分离技术。如下图所示,对淡化膜右侧的海水加压,水分子可以透过淡化膜进入左侧淡水池,而海水中的各种离子不能通过淡化膜,从而得到淡水。对加压后右侧海水成分变化进行分析,正确的是( )
海水淡化可以采用膜分离技术。如下图所示,对淡化膜右侧的海水加压,水分子可以透过淡化膜进入左侧淡水池,而海水中的各种离子不能通过淡化膜,从而得到淡水。对加压后右侧海水成分变化进行分析,正确的是( )
A. 溶质的质量增加 B. 溶剂的质量减少
C. 溶液的质量不变 D. 溶质的质量分数减少
26.取碳酸钠和氯化钠的固体混合物13.6g,与一定质量的稀盐酸恰好完全反应,得到10%的氯化钠溶液147g。计算:(1)固体混合物中碳酸钠的质量分数;(2)生成二氧化碳的质量;(3)该盐酸的溶质的质量分数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com