
4. (2006重庆)设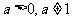 ,函数
,函数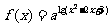 有最大值,则不等式
有最大值,则不等式
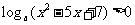 的解集为 。
的解集为 。
3.(2005辽宁)若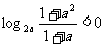 ,则
,则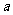 的取值范围是( )
的取值范围是( )
A.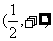 B.
B.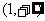 C.
C.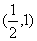 D.
D.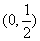
[填空题]
2.(2006江西6)若不等式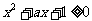 对一切
对一切 成立,则
成立,则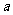 的最小值为( )
的最小值为( )
A.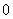 B.
B. C.
C.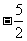 D.
D. 
1.(2004年天津卷)不等式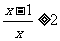 的解集为 ( )
的解集为 ( )
A.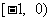 B.
B. C.
C. D.
D.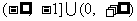
1、 含参数不等式的基本途径是分类讨论
(1)要考虑参数的总的取值范围
(2)用同一标准对参数进行划分,做到不重不漏。
同步练习 6.5不等式解法举例
[选择题]
2、解分式不等式时注意先化为标准式,使右边为0;
1、解不等式基本思想是化归转化;
[例1]已知关于x的不等式(a+b)x+(2a-3b)<0解为(-∞,-1/3),求关于x的不等式(a-3b)x+(b-2a)>0的解集。
解:由(a+b)x<(2a-3b)解集为(-∞,-1/3),
∴a+b>0,且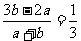 ,从而a=2b.
,从而a=2b.
又a+b=3b>0,∴b>0,将a=2b代入(a-3b)x+(b-2a)>0
得-bx-3b>0,x<-3,所求解集为(-∞,-3)。
思维点拨:挖掘隐含条件a+b>0很重要。
[例2] 若不等式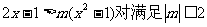 的所有m都成立。求x的取值范围。
的所有m都成立。求x的取值范围。
[解]原不等式化为(x2-1)m-(2x-1)<0记f(m)=(x2-1)m-(2x-1)
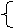 (-2≤m≤2),根据题意有 f(-2)=-2(x2-1)-(2x-1)<0
(-2≤m≤2),根据题意有 f(-2)=-2(x2-1)-(2x-1)<0
f(2)=2(x2-1)-(2x-1)<0
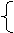 即 2x2+2x-3>0
即 2x2+2x-3>0
2x2-2x-1<0
解之,x的取值范围为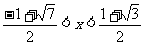
思维点拨:从表面上看,这是一个关于x的一元二次不等式,实际上是一个关于m的一元一次不等式,并且已知它的解集为[-2,2],求参数x的取值范围。
[例3]
(2005江西) 已知函数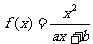 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;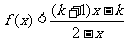
解:(1)将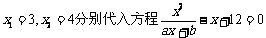 得
得
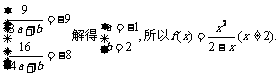
(2)不等式即为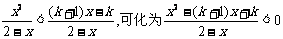
即
①当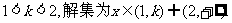
②当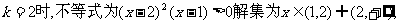
③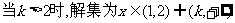 .
.
提炼方法:穿根法,依k在数轴上的位置,分类讨论. 不等式与函数的综合是最常见的题目,要多留心这类问题的解法。
[例4]解关于x的不等式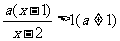
[解]原不等式等价于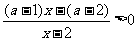
∵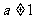 ∴等价于:
∴等价于: (*)
(*)
当a>1时,(*)式等价于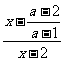 >0
>0
∵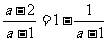 <1∴x<
<1∴x<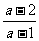 或x>2
或x>2
a<1时,(*)式等价于 <0
<0
由2-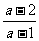 =
=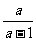 知:
知:
当0<a<1时,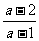 >2,∴2<x<
>2,∴2<x<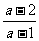 ;
;
当a<0时,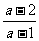 <2,∴
<2,∴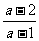 <x<2;
<x<2;
当a=0时,当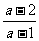 =2,∴x∈φ
=2,∴x∈φ
综上所述可知:当a<0时,原不等式的解集为(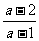 ,2);
,2);
当a=0时,原不等式的解集为φ;
当0<a<1时,原不等式的解集为(2,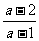 );
);
当a>1时,原不等式的解集为(-∞,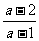 )∪(2,+∞)。
)∪(2,+∞)。
温馨提示::1.含参数不等式,对所含字母分类讨论,不重不漏;
2.含参数的二次不等式讨论的项目依次是:
(1)二次项系数,(2)有根无根,(3)根的大小.
[研讨.欣赏](2003黄冈模拟)已知函数f(x)=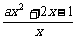 的定义域恰为不等式log2(x+3)+log
的定义域恰为不等式log2(x+3)+log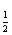 x≤3的解集,且f(x)在定义域内单调递减,求实数a的取值范围.
x≤3的解集,且f(x)在定义域内单调递减,求实数a的取值范围.
解:由log2(x+3)+log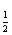 x≤3得
x≤3得
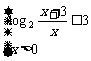
 x≥
x≥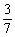 ,
,
即f(x)的定义域为[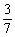 ,+∞).
,+∞).
∵f(x)在定义域[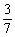 ,+∞)内单调递减,
,+∞)内单调递减,
∴当x2>x1≥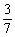 时,f(x1)-f(x2)>0恒成立,即有
时,f(x1)-f(x2)>0恒成立,即有
(ax1-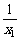 +2)-(ax2-
+2)-(ax2-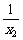 +2)>0
+2)>0
 a(x1-x2)-(
a(x1-x2)-(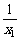 -
-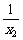 )>0
)>0
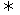 (x1-x2)(a+
(x1-x2)(a+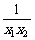 )>0恒成立.
)>0恒成立.
∵x1<x2,∴(x1-x2)(a+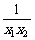 )>0
)>0
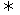 a+
a+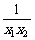 <0.
<0.
∵x1x2>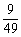
 -
-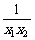 >-
>-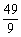 ,
,
要使a<-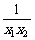 恒成立,
恒成立,
则a的取值范围是a≤-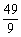 .
.
5. 答案:(-3-2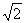 ,-3+2
,-3+2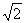 )∪{1}; 6. (0,loga3)
)∪{1}; 6. (0,loga3)
6. 设 ,函数
,函数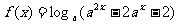 ,则使
,则使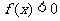 的
的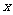 的取值范围是___________
的取值范围是___________
简答:1-4.BACA; 4.法1:代入判断法,将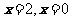 分别代入不等式中,判断关于
分别代入不等式中,判断关于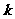 的不等式解集是否为
的不等式解集是否为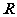 ;
;
法2:求出不等式的解集:
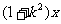 ≤
≤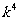 +4
+4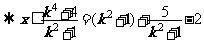
 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com