7．下列各句中，没有语病的一句是

(　)

A．我国粮食的生产，长期都能做到自给，对有着十几亿人口的大国来说，是十分不易的，这与科学家袁隆平的巨大贡献是密不可分的。

B．某报记者一篇报道地方强制拆迁，侵害群众利益的文章，惹恼了当地官员，他们竟派公安人员到报社拘传记者，其根本原因是滥用公权在作怪。

C．“梁山伯与祝英台”这个优美而凄婉的传奇爱情故事，流传年代久远，流传地域很广，可以说是家喻户晓，老少妇孺皆知。

D．我省药品食品监督部门已着手对全省食品生产企业按照诚信度等级进行分类管理，不良记录的多少，将直接影响企业的诚信等级。

[解析]　A项搭配不当，“粮食的生产”与“自给”不能搭配。可将“粮食的生产”改成“生产的粮食”。B项句式杂糅，可去掉“在作怪”。C项成分赘余，可删去“老少”。

[答案]　D

6．下列各句中，没有语病的一句是

　 (　)

A．“倒爷”这个词语对许多俄罗斯人并不陌生，在上个世纪90年代，一群带着大包小包来往于中俄边境做生意的人被冠以这种特定的称谓。

B．据报道，这项耗资4.2亿美元的火星探测项目由美国宇航局喷气推进实验室研究开发，其中，“凤凰”号探测器着陆火星是最关键的一环。

C．相关统计数字表明，全球手机用户年平均增长率为22%，今年全球手机使用者数量已超过33亿左右，在全球人口中的普及率达到49%。

D．面对大学校园信仰缺失、开口闭口“股票”“金钱”，纪宝成指出：大学只有保持宁静，才能以高质量的人才培养和科学研究引领社会进步。

[解析]　A项主客体颠倒，应为“许多俄罗斯人对‘倒爷’这个词语并不陌生”；C项“超过……左右”矛盾；D项成分残缺，在“金钱”后加“的现状”。

[答案]　B

5．下列各句中，没有语病的一句是

(　)

A．两会代表们期盼国家医药管理局尽快制定措施，尽量降低药品的价格和流通环节，让老百姓能看得起病，更好地解决老百姓看病难的问题。

B．中国2010年上海世博会将是一次探讨新世纪人类城市生活的伟大盛会，将是一曲以“创新”和“融合”为主旋律的交响乐，将成为人类文明的一次精彩对话。

C．中国载人航天工程的基本要素包括航天员、飞船应用、载人飞船、运载火箭、发射场、测控通信和着陆场七大系统组成。

D．青岛从被定为2008年奥帆赛、残奥帆赛举办城市的那天起，备受关注的志愿者选拔工作就有条不紊地开展着，随着赛事的日益临近，志愿者团队主体将浮出水面。

[解析]　A项“降低”和“环节”搭配不当；C项“包括……组成”杂糅；D项偷换主语，将“从”调至句首。

[答案]　B

4．下列各句中，没有语病的一句是　

　(　)

A．山东省政府建议确立中华文化标志城的国家级文化功能地位，成为举行国家重要文化庆典和重大文化活动的法定场所之一。

B．中国驻韩大使在圣火传递活动即将举行之际接受记者专访，希望代表和平、友谊和进步的奥运圣火能传递和促进人类共同的梦想与中韩之间的友谊。　

C．国际互联网虽然给我们带来了不少商务、交通上的便利，但是我们对网上信息的真实性和安全性越来越怀疑。

D．胶济铁路列车脱轨事故发生后，铁道部启动紧急预案，迅速组织救援，做好对事故列车旅客的安置工作，以最快速度恢复正常行车。

[解析]　A项，成分残缺，应为“使其成为……之一”。B项，搭配不当，应为“传递……梦想”，“促进……友谊”。C项，语序不当，“虽然”应放在句首，“不少”应移到“便利”前。

[答案]　D

3．下列各句中，句意明确、没有语病的一句是　

　(　)

A．北京奥运会火炬接力的主题是“和谐之旅”，它向世界表达了中国人民对内致力于构建和谐社会，对外努力建设和平繁荣的美好世界。

B．参加世界杯预选赛的国脚们十分清楚，一场球的输赢，不仅关系到祖国的荣誉，而且关系到个人的尊严。

C．当需要建筑师或景观设计师将文化具体化的时候，我们习惯于把眼光投向城市与场地的久远历史--百年、千年、甚至万年。

D．国家将尝试建立国家规划监督员制度和国家级专项保护资金，以充分发挥国家对历史文化名城的保护和监督。

[解析]　A项成分残缺，“表达”缺少宾语，可在句末加上“的愿望”；B项递进关系颠倒，“不仅关系到祖国的荣誉，而且关系到个人的尊严”应改为“不仅关系到个人的尊严，而且关系到祖国的荣誉”；D项“建立”与“保护资金”搭配不当，“发挥”后缺宾语“职能”或“作用”之类。

[答案]　C

1．下列句子中，没有语病的一项是

(　)

A．艺术家能把自己心灵的创伤和对社会现状的痛苦感受，毫无顾忌地倾泻出来，靠的是以艺术来直接表达的。

B．如果说奥运会开幕式上，击缶倒计时的独特创意给了世人一个惊喜，那么闭幕式上，采用烟花技术在天空“画”倒计时数字，则让人们叹为观止。

C．孩子们对“动漫”的情有独钟，推动着“动漫”产业朝着高质量、高速度、高赢利发展，嗅觉灵敏的商家对此更是推波助澜。

D．以生漆为底层的彩绘陶质文物保护是一个世界难题，没有任何的经验和技术可以借鉴，秦俑如何将艳丽的彩绘保留下来成为当务之急。

[解析]　 A项句式杂糅，“靠的是以艺术来直接表达的”可以改为“靠的是艺术”或者“是用艺术来直接表达的”。C项缺中心词，“高质量、高速度、高赢利”后应加“方向”一词。另外“推波助澜”多含贬义。D项末句简化为“秦俑成为当务之急”主谓搭配不当，应是“艳丽的秦俑彩绘如何保留下来成为当务之急”。

[答案]　B

12.(文)已知函数f(x)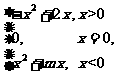＝是奇函数.

(1)求实数m的值；

(2)若函数f(x)的区间[－1，a－2]上单调递增，求实数a的取值范围.

解：(1)设x<0，则－x>0，

所以f(－x)＝－(－x)²+2(－x)＝－x²－2x.

又f(x)为奇函数，所以f(－x)＝－f(x)，

于是x<0时，f(x)＝x²+2x＝x²+mx，

所以m＝2.

(2)要使f(x)在[－1，a－2]上单调递增，

结合f(x)的图象知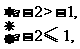

所以1＜a≤3，故实数a的取值范围是(1,3].

(理)已知定义域为R的函数f(x)＝是奇函数.

(1)求a、b的值；

(2)若对任意的t∈R，不等式f(t²－2t)+f(2t²－k)<0恒成立，求k的取值范围.

解：(1)因为f(x)是R上的奇函数，所以f(0)＝0，

即＝0，解得b＝1，从而有f(x)＝.

又由f(1)＝－f(－1)，知＝－，解得a＝2.

故a＝2，b＝1.

(2)由(1)知f(x)＝＝－+.

由上式易知f(x)在(－∞，+∞)上为减函数.

又因f(x)是奇函数，

从而不等式f(t²－2t)+f(2t²－k)<0

等价于f(t²－2t)<－f(2t²－k)＝f(－2t²+k).

因f(x)是减函数，由上式推得t²－2t>－2t²+k，

即对一切t∈R有3t²－2t－k>0.

从而判别式Δ＝4+12k<0，解得k<－.

11.(2009·山东高考)已知定义在R上的奇函数f(x)满足f(x－4)＝－f(x)，且在区间[0,2]　　　　　　　　 上是增函数.若方程f(x)＝m(m＞0)在区间[－8,8]上有四个不同的根x₁，x₂，x₃，x₄，　　　　 则x₁+x₂+x₃+x₄＝　　.

　　 解析：由f(x－4)＝－f(x)⇒f(4－x)＝f(x)，

　　 故函数图象关于直线x＝2对称，

　　 又函数f(x)在[0,2]上是增函数，且为奇函数，

　　 故f(0)＝0，故函数f(x)在(0,2]上大于0，

　　 根据对称性知函数f(x)在[2,4)上大于0，

　　 同理推知函数f(x)在(4,8)上小于0，故在区间(0,8)上方程f(x)＝m(m＞0)的两根关于　 直线x＝2对称，

　　 故此两根之和等于4，

　　 根据f(x－4)＝－f(x)⇒f(x－8)＝－f(x－4)＝f(x)，

　　 函数f(x)以8为周期，

　　 故在区间(－8,0)上方程f(x)＝m(m＞0)的两根关于直线x＝－6对称，此两根之和等　 于－12，

　　 综上四个根之和等于－8.

　　 答案：－8

10.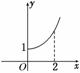(2009·福建高考)定义在R上的偶函数f(x)的部分图象如右图所示，

则在(－2,0)上，下列函数中与f(x)的单调性不同的是　　　 (　)

A.y＝x²+1

B.y＝|x|+1

C.y＝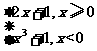

D.y＝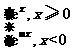

解析：∵f(x)为偶函数，由图象知，

f(x)在(－2,0)上为减函数，

而y＝x³+1在(－∞，0)上为增函数，故选C.

答案：C