
3.当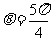 时,
时, 的值是____.
的值是____.
作业的答案与提示:
2.化简: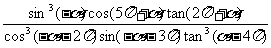
1.求下列三角函数值:
(1)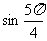 ; (2)
; (2)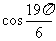 ;(3)
;(3)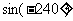 ;(4)
;(4)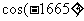
2.化简sin(-2)+cos(-2-π)·tan(2-4π)所得的结果是( )
(A)2sin2 (B)0 (C)-2sin2 (D) -1
答案:C
选题目的:熟练掌握诱导公式一、二、三及同角三角函数关系中商数关系的灵活运用.
使用方法:供课堂练习用.
评估:本题不仅涉及了诱导公式一、二、三,而且还涉及了同角三角函数的关系,此外还出现了如“sin(-2)”这样的学生较为陌生的三角函数值,求解时若只计算一次便获得准确结果,表明在新知识的运用和旧知识的记忆方面都达到了较好的程度.
1.求下式的值:2sin(-1110º) -sin960º+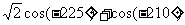
答案:-2
提示:原式=2sin(-30º)+sin60º- =-2
=-2
选题目的:通过本题练习,使学生熟练诱导公式一、二、三的运用.
使用方法:供课堂练习用.
评估:求解本题时,在灵活地进行角的配凑,使之符合诱导公式中角的结构特点方面有着较高的要求.若只计算一次便获得准确结果,表明在利用诱导公式一、二、三求解三角函数式的值方面已达到了较熟练的程度.
例1.下列三角函数值: (1)cos210º; (2)sin
分析:本题是诱导公式二的巩固性练习题.求解时,只须设法将所给角分解成180º+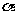 或(π+
或(π+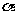 ),
),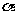 为锐角即可.
为锐角即可.
解:(1)cos210º=cos(180º+30º)=-cos30º=-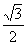 ;
;
(2)sin =sin(
=sin(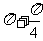 )=-sin
)=-sin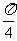 =-
=-

例2.求下列各式的值: (1)sin(-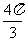 );(2)cos(-60º)-sin(-210º)
);(2)cos(-60º)-sin(-210º)
分析:本题是诱导公式二、三的巩固性练习题.求解时一般先用诱导公式三把负角的正弦、余弦化为正角的正弦、余弦,然后再用诱导公式二把它们化为锐角的正弦、余弦来求.
解:(1)sin(-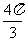 )=-sin(
)=-sin(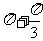 )=sin
)=sin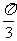 =
=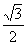 ;
;
(2)原式=cos60º+sin(180º+30º)=cos60º-sin30º=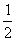 -
-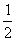 =0
=0
例3.化简
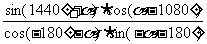
分析:这是诱导公式一、二、三的综合应用.适当地改变角的结构,使之符合诱导公式中角的形式,是解决问题的关键.
解
例4.已知cos(π+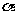 )=-
)=- 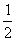 ,
,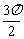 <
<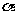 <2π,则
<2π,则
nqin(2π-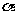 )的值是( ).
)的值是( ).
(A)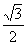 (B)
(B)
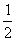 (C)-
(C)-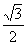 (D)±
(D)±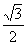
分析:通过本题的求解,可进一步熟练诱导公式一、二、三的运用.求解时先用诱导公式二把已知条件式化简,然后利用诱导公式一和三把sin(2π-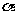 )化成-sin
)化成-sin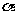 ,再用同角三角函数的平方关系即可.
,再用同角三角函数的平方关系即可.
事实上,已知条件即cos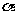 =
=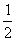 ,于是
,于是
sin(2π-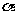 )=-sin
)=-sin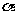 =-(-
=-(- )=
)= =
=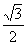
因此选A
公式二: 用弧度制可表示如下:
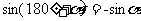
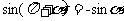
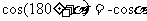
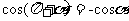

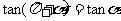
它刻画了角180º+ 与角
与角 的正弦值(或余弦值)之间的关系,这个关系是:以角
的正弦值(或余弦值)之间的关系,这个关系是:以角 终边的反向延长线为终边的角的正弦值(或余弦值)与角
终边的反向延长线为终边的角的正弦值(或余弦值)与角 的正弦值(或余弦值)是一对相反数.这是因为若设
的正弦值(或余弦值)是一对相反数.这是因为若设 的终边与单位圆交于点P( x,y),则角
的终边与单位圆交于点P( x,y),则角 终边的反向延长线,即180º+
终边的反向延长线,即180º+ 角的终边与单位圆的交点必为P´(-x,-y)(如图4-5-1).由正弦函数、余弦函数的定义,即可得sin
角的终边与单位圆的交点必为P´(-x,-y)(如图4-5-1).由正弦函数、余弦函数的定义,即可得sin =y, cos
=y, cos =x,
=x,
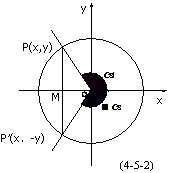 sin(180º+
sin(180º+ )=-y, cos(180º+
)=-y, cos(180º+ )=-x,
)=-x,
所以 :sin(180º+ )=-sin
)=-sin ,cos(180º+
,cos(180º+ )=-cos
)=-cos .
.
公式三: 
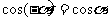
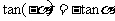
它说明角- 与角
与角 的正弦值互为相反数,而它们的余弦值相等.这是因为,若没
的正弦值互为相反数,而它们的余弦值相等.这是因为,若没 的终边与单位圆交于点P(x,y),则角-
的终边与单位圆交于点P(x,y),则角- 的终边与单位圆的交点必为P´(x,-y)(如图4-5-2).由正弦函数、余弦函数的定义,即可得
的终边与单位圆的交点必为P´(x,-y)(如图4-5-2).由正弦函数、余弦函数的定义,即可得
sin =y, cos
=y, cos =x,
=x,
sin(- )=-y,
cos(-
)=-y,
cos(- )=x,
)=x,
所以:sin(- )= -sin
)= -sin , cos(-
, cos(- )= cosα
)= cosα
公式二、三的获得主要借助于单位圆及正弦函数、余弦函数的定义.根据点P的坐标准确地确定点P´的坐标是关键,这里充分利用了对称的性质.事实上,在图1中,点P´与点P关于原点对称,而在图2中,点P´与点P关于x轴对称.直观的对称形象为我们准确写出P´的坐标铺平了道路,体现了数形结合这一数学思想的优越性.
公式四: 用弧度制可表示如下:

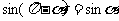
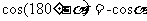
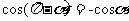
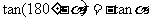
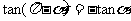
公式五:
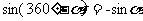
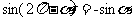


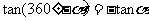
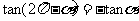
这两组公式均可由前面学过的诱导公式直接推出(公式四可由公式二、三推出,公式五可由公式一、三推出),体现了把未知问题化为已知问题处理这一化归的数学思想.公式的推导并不难,然而推导中的化归意识和策略是值得我们关注的.
五组诱导公式可概括为:
 +k·360º(k∈Z),-
+k·360º(k∈Z),- ,180º±
,180º± ,360º-
,360º- 的三角函数值,等于
的三角函数值,等于 的同名函数值,前面加上一个把
的同名函数值,前面加上一个把 看成锐角时原函数值的符号.
看成锐角时原函数值的符号.
这里的“同名三角函数值”是指等号两边的三角函数名称相同;“把 看成锐角”是指
看成锐角”是指 原本是任意角,这里只是把它视为锐角处理;“前面加上一个……符号”是指
原本是任意角,这里只是把它视为锐角处理;“前面加上一个……符号”是指 的同名函数值未必就是最后结果,前面还应添上一个符号(正号或负号,主要是负号,正号可省略),而这个符号是把任意角
的同名函数值未必就是最后结果,前面还应添上一个符号(正号或负号,主要是负号,正号可省略),而这个符号是把任意角 视为锐角情况下的原角原函数的符号.应注意讲清这句话中每一词语的含义,特别要讲清为什么要把任意角α看成锐角.建议通过实例分析说明.
视为锐角情况下的原角原函数的符号.应注意讲清这句话中每一词语的含义,特别要讲清为什么要把任意角α看成锐角.建议通过实例分析说明.
诱导公式一:
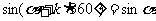
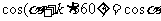
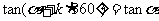 (其中
(其中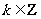 )
)
用弧度制可写成
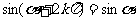
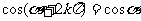
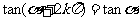 (其中
(其中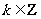 )
)
诱导公式(一)的作用:把任意角的正弦、余弦、正切化为0º―360º之间角的正弦、余弦、正切,其方法是先在0º―360º内找出与角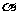 终边相同的角,再把它写成诱导公式(一)的形式,然后得出结果
终边相同的角,再把它写成诱导公式(一)的形式,然后得出结果
这组公式可以统一概括为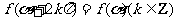 的形式,其特征是:等号两边是同名函数,且符号都为正
的形式,其特征是:等号两边是同名函数,且符号都为正
由这组公式还可以看出,三角函数是“多对一”的单值对应关系,明确了这一点,为今后学习函数的周期性打下基础
3.运用公式时,注意“弧度”与“度”两种度量制不要混用,如写成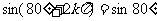 ,
,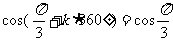 是不对的.
是不对的.
具有完全相同的组成的原子排列,但互为镜像,在三维空间不能重叠的分子,互称为
。有手性异体的分子叫手性分子。
思考:形成手性异构的条件?
无机含氧酸的酸性:
通常在无机含氧酸中非羟氧的数目 ,酸性越强;对于同一种元素的含氧酸,
该元素的 越高,含氧酸酸性越强。
试题枚举
[例1]下列分子的立体结构,其中属于直线型分子的是 ( )
A.H2O B.CO2 C.C2H2 D. P4
解析:多原子分子若要属于直线型分子,中心原子应采用sp杂化,且无孤对电子
答案:B C。
[例2]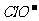 、
、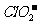 、
、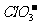 、
、 中Cl都是以sp3杂化轨道与O原子成键的,试推测下列微粒的立体结构
中Cl都是以sp3杂化轨道与O原子成键的,试推测下列微粒的立体结构
|
微粒 |
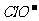 |
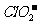 |
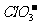 |
 |
|
立体结构 |
|
|
|
|
解析:杂化轨道数相同,但孤对电子数同
答案:直线;V型;三角锥形;正四面体
[例3]下列物质的分子中,键角最小的是
A.H2O B.BF3 C.NH3 D.CH4
解析:BF3中的硼为sp2杂化,无孤对电子,键角120°;H2O、NH3、CH4中中心原子均为sp3杂化,H2O 中有两对孤对电子,对共用电子对“压迫”较大,键角最小
答案:A
[例4]铵根离子中存在的化学键类型按离子键、共价键和配位键分类,应含有
A.离子键和共价键 B.离子键和配位键 C.配位键和共价键 D.离子键
解析:铵根离子中N原子最外层5个电子,采用sp3杂化形成4个杂化轨道,其中一个杂化轨道被孤对电子占据,与H+的空轨道形成配位键;另三个轨道与H形成共价键
答案:C
[例5]根据“相似相溶”规律,你认为下列物质在水中溶解度较大的是( )
A .乙烯 B .二氧化碳 C.二氧化硫 D.氢气
解析:A B D非极性分子。
答案:C
[例6]下列氯元素含氧酸酸性最强的是 ( )
A.HClO B.HClO2 C.HClO3 D.HClO4
解析: D分子中非羟基氧数目大。
答案:D
[例7]在有机物分子中,若某个碳原子连接着四个不同的原子或原子团,这种碳原子称为“手性碳原子”。凡有一个手性碳原子的物质一定具有光学活性,物质
 CH3COOCH2-CH-CHO有光学活性,发生下列反应后生成的有机物无光学活性的是
CH3COOCH2-CH-CHO有光学活性,发生下列反应后生成的有机物无光学活性的是
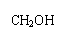
A.与甲酸发生酯化反应 B.与NaOH水溶液共热
C.与银氨溶液作用 D.在催化剂存在下与H2作用
解析: 手性碳原子应连接着四个不同的原子或原子团
答案:B D
正电中心和负电中心不重合的分子叫 分子,分子的极性来自化学键的极性,只含非极性键的分子一定是非极性分子;含有极性键的分子是否具有极性可根据极性键的极性的 是否等于零来判断。
思考:为什么BF3是非极性分子而NH3是极性分子?
非极性溶质一般易溶于 ,极性溶质一般易溶于 ,这一经验规律叫做“相似相溶”,若溶质与溶剂分子能形成氢键,则溶解性好。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com