
2.关于加速度的方向,下列说法中正确的是( )
A.总与初速度方向一致
B.总与平均速度方向一致
C.总与速度变化的方向一致
D.总与位移的方向一致
[解析] 加速度的方向与速度变化的方向一致,与初速度、平均速度及位移的方向没有关系.
[答案] C
1.关于加速度的概念,下列说法正确的是( )
A.加速度就是加出来的速度
B.加速度反映了速度变化的大小
C.加速度反映了速度变化的快慢
D.加速度为正值,表示速度的大小一定越来越大
[解析] 加速度是反映速度变化快慢的物理量,等于速度的变化量与所用时间的比值,而速度变化量的大小与所取时间长短无关,故C正确,B错误.加速度为正值,说明加速度的方向与所取正方向一致,这与速度变大变小无关.速度是否增加,取决于加速度方向与速度方向的关系,故D错.
[答案] C
4.速度变化快慢的描述--加速度

(本栏目内容,在学生用书中以活页形式分册装订!)
15.已知双曲线x2-y2=2的右焦点为F,过点F的动直线与双曲线相交于A、B两点,点C的坐标是(1,0).
(Ⅰ)证明: ·为常数;
(Ⅱ)若动点M满足=++(其中O为坐标原点),求点M的轨迹方程.
解:由条件知F(2,0),设A(x1,y1),B(x2,y2).
(Ⅰ)当AB与x轴垂直时,可设点A、B的坐标分别为(2,)、(2,-),此时·=(1,)·(1,-)=-1.
当AB不与x轴垂直时,设直线AB的方程是y=k(x-2)(k≠±1).
代入x2-y2=2有(1-k2)x2+4k2x-(4k2+2)=0.
则x1、x2是上述方程的两个实根,所以x1+x2=,x1x2=.
于是·=(x1-1)(x2-1)+y1y2
=(x1-1)(x2-1)+k2(x1-2)(x2-2)
=(k2+1)x1x2-(2k2+1)(x1+x2)+4k2+1
=-+4k2+1
=(-4k2-2)+4k2+1=-1.
综上所述,·为常数-1.
(Ⅱ)解法一:设M(x,y),则=(x-1,y),=(x1-1,y1),=(x2-1,y2),=(-1,0).由=++得:,即
于是AB的中点坐标为(,).
当AB不与x轴垂直时,==,即y1-y2=(x1-x2).
又因为A、B两点在双曲线上,所以x-y=2,x-y=2,两式相减得
(x1-x2)(x1+x2)=(y1-y2)(y1+y2),即(x1-x2)(x+2)=(y1-y2)y.
将y1-y2=(x1-x2)代入上式,化简得x2-y2=4.
当AB与x轴垂直时,x1=x2=2,求得M(2,0),也满足上述方程.
所以点M的轨迹方程是x2-y2=4.
解法二:同解法一得.①
当AB不与x轴垂直时,由(Ⅰ)有x1+x2=,②
y1+y2=k(x1+x2-4)=k(-4)=.③
由①、②、③得x+2=, ④
y=.⑤
当k≠0时,y≠0,由④、⑤得,=k,将其代入⑤有y==.整理得x2-y2=4.
当k=0时,点M的坐标为(-2,0),满足上述方程.
当AB与x轴垂直时,x1=x2=2,求得M(2,0),也满足上述方程.
故点M的轨迹方程是x2-y2=4.
14.已知两条直线l1:2x-3y+2=0和l2:3x-2y+3=0,有一动圆(圆心和半径都动)与l1、l2都相交,且l1、l2被圆截得的弦长分别是定值26和24,求圆心的轨迹方程.
解:设动圆的圆心为M(x,y),半径为r,点M到直线l1,l2的距离分别为d1和d2.
由弦心距、半径、半弦长间的关系得,
即
消去r得动点M满足的几何关系为d-d=25,
即-=25.
化简得(x+1)2-y2=65.
此即为所求的动圆圆心M的轨迹方程.
13.
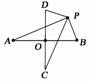
如右图所示,线段AB与CD互相垂直平分于点O,|AB|=2a(a>0),|CD|=2b(b>0),动点P满足|PA|·|PB|=|PC|·|PD|.求动点P的轨迹方程.
解:以O为坐标原点,直线AB、CD分别为x轴、y轴建立直角坐标系,

12.
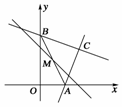
如右图所示,已知点C的坐标是(2,2),过点C的直线CA与x轴交于点A,过点C且与直线CA垂直的直线CB与y轴交于点B.设点M是线段AB的中点,求点M的轨迹方程.
解法一:(参数法):设M的坐标为(x,y).
若直线CA与x轴垂直,则可得到M的坐标为(1,1).
若直线CA不与x轴垂直,设直线CA的斜率为k,则直线CB的斜率为-,故直线CA方程为:y=k(x-2)+2,
令y=0得x=2-,则A点坐标为(2-,0).
CB的方程为:y=-(x-2)+2,令x=0,得y=2+,
则B点坐标为(0,2+),由中点坐标公式得M点的坐标为①
消去参数k得到x+y-2=0(x≠1),
点M(1,1)在直线x+y-2=0上,
综上所述,所求轨迹方程为x+y-2=0.
解法二:(直接法)设M(x,y),依题意A点坐标为(2x,0),B点坐标为(0,2y).
∵|MA|=|MC|,
∴=,
化简得x+y-2=0.
解法三:(定义法)依题意|MA|=|MC|=|MO|,
即:|MC|=|MO|,所以动点M是线段OC的中垂线,故由点斜式方程得到:x+y-2=0.
11.已知△ABC的边AB长为6,点C到A、B两点的距离之比为2∶1,则点C的轨迹方程为________.
答案:(x-5)2+y2=16(y≠0)
解析:
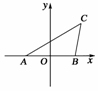
以AB所在直线为x轴,线段AB中点为原点,建立平面直角坐标系,则A(-3,0),B(3,0).设C(x,y),
由题意=2,
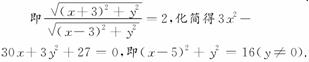
10.平面上有三点A(-2,y),B(0,),C(x,y),若⊥,则动点C的轨迹方程为________.
答案:y2=8x
解析:=(2,-), =(x,).
∵⊥,∴·=0,得2·x-·=0,
得y2=8x.
9.已知△ABC的顶点B(0,0),C(5,0),AB边上的中线长|CD|=3,则顶点A的轨迹方程为________.
答案:(x-10)2+y2=36(y≠0)
解法一:直接法,设A(x,y),y≠0,则D(,),
∴|CD|==3,
化简得:(x-10)2+y2=36,由于A、B、C三点构成三角形,
所以A不能落在x轴上,即y≠0.
解法二:

定义法.如右图所示,设A(x,y),D为AB的中点,过A作AE∥CD交x轴于E,
∵|CD|=3,∴|AE|=6,则E(10,0)
∴A到E的距离为常数6,
∴A的轨迹为以E为圆心,6为半径的圆,
即(x-10)2+y2=36,又A、B、C不共线,故A点纵坐标y≠0,
故A点轨迹方程为(x-10)2+y2=36(y≠0).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com