
1.下列各组词语中加点字的注音,全都正确的一组是 ( )
A.吮(shǔn)吸 果实累累(léi ) 订(dīng)正 心宽体胖(pán)
B.谙(ān)练 戛(jiá)然而止 针灸(jiū) 博闻强识(zhì)
C.拮据(jū) 颓壁残垣(yuán) 矗立(chù) 力能扛(gāng)鼎
D.顷刻(qīng) 酩酊(dǐng)大醉 宽宥(yòu) 一哄(hōng)而散
25. 抛物线
抛物线 与直线y=x+1交于A、C两点,与y轴交于B,AB∥x轴,且
与直线y=x+1交于A、C两点,与y轴交于B,AB∥x轴,且 ,(1)求抛物线的解析式。
,(1)求抛物线的解析式。

(2)P为x轴负半轴上一点,以AP、AC为边作 ,是否存在P,使得Q点恰好在此抛物线上?若存在,请求出P、Q的坐标;若不存在,请说明理由。
,是否存在P,使得Q点恰好在此抛物线上?若存在,请求出P、Q的坐标;若不存在,请说明理由。
(3)AD⊥X轴于D,以OD为直径作⊙M,N为⊙M上一动点,(不与O、D重合),过N作AN的垂线交x轴于R点,DN交Y轴于点S,当N点运动时,线段OR、OS是否存在确定的数量关系?写出证明。
24.图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合)。
(1)操作:固定△ABC,将△C′D′E′绕点C顺时针旋转30°得到△CDE,连结AD、BE,CE的延长线交AB于F(图2);
探究:在图2中,线段BE与AD之间有怎样的大小关系?试证明你的结论。
(2)操作:将图2中的△CDE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR(图3);
请问:经过多少时间,△PQR与△ABC重叠部分的面积恰好等于 ?
?
(3)操作:图1中△C′D′E′固定,将△ABC移动,使顶点C落在C′E′的中点,边BC交D′E′于点M,边AC交D′C′于点N,设∠AC C′=α(30°<α<90,图4);
探究:在图4中,线段C N·E
N·E M的值是否随α的变化而变化?如果没有变化,请你求出C
M的值是否随α的变化而变化?如果没有变化,请你求出C N·E
N·E M的值,如果有变化,请你说明理由。
M的值,如果有变化,请你说明理由。

23.已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产甲、乙两种型号的时装共80套.已知做一套甲种型号的时装或一套乙种型号的时装所需A、B两种布料如下表:
|
布料 时装 |
甲 |
乙 |
|
A种(米) |
0.6 |
1.1 |
|
B种(米) |
0.9 |
0.4 |
若销售一套甲种型号的时装可获利润45元,销售一套乙种型号的时装可获利润50元.设生产乙种型号的时装为x套,用这批布料生产这两种型的时装所为y元.
(1)写出y(元)与x(套)的函数关系式,并写出自变量的取值范围;
(2)雅美服装厂在生产这批时装中,当生产两种型号的时装各多少套时,获得的总利润最大?最大利润是多少元?
22. 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF ∥AC交BA的延长线于F.
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF ∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB = 15,EF = 10,求AE的长.
21.已知点A(2, )在直线
)在直线 上.
上.
(1)点A(2, )向左平移3个单位后的坐标是
;直线
)向左平移3个单位后的坐标是
;直线 向左平移3个单位后的直线解析式是
;
向左平移3个单位后的直线解析式是
;
(2)点A(2, )绕原点顺时针旋转90°所走过的路径长为__________;
)绕原点顺时针旋转90°所走过的路径长为__________;
(3)求直线 绕点P(-1,0)顺时针旋转90°后的直线解析式.
绕点P(-1,0)顺时针旋转90°后的直线解析式.
20.武汉某中学2009年元旦晚会上,主持人安排了抽奖活动.具体方法是:设置如下表所示的翻板,每次抽奖翻开一个数字,数字背面写有所中奖品或新年祝词.
|
1 |
2 |
3 |
|
4 |
5 |
6 |
|
7 |
8 |
9 |
|
奖MP4一个 |
万事如意 |
学业进步 |
|
身体健康 |
新年快乐 |
奖MP3一个 |
|
奖笔记本一个 |
奖钢笔一支 |
心想事成 |
(1)主持人想知道“第一个人抽奖中奖”的概率,而且觉得翻版牌太麻烦,请你设计一个简便的模拟抽奖方法,并估计“第一个人抽奖中奖”的概率.
(2)若晚会开始前给每名入场的学生发一张入场券,其中有100张后标有“新年快乐”.晚会进行中主持人任意邀请台下50名同学上台合唱“同一首歌”,并宣布这50名同学的入场券后标有“新年快乐”的参与抽奖,结果有4人中奖,中奖率为40%,请估计参加本次晚会的学生人数.
19.已知:如图,已知:D是△ABC的边AB上一点,CN∥AB,DN交AC于,若MA=MC,
求证:CD=AN.
18.先化简,再求值: 并代入你喜欢且有意义的x值。
并代入你喜欢且有意义的x值。

17.解方程: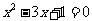
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com