
18、(1)证明:……(略)……………………………………………………5分
(2)证明:……(略)……………………………………………………4分
17、解:原式=
=2(a+1)-(a-1)
=2a+2-a+1
=a+3………………………………………………………………6分
当a=cot30°=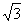 时……………………………………………8分
时……………………………………………8分
原式= ……………………………………………………9分
……………………………………………………9分
说明:只要化简正确给6分。
11、5.8×105 12、3(x+3)(x-3) 13、x>2 14、25° 15、2π 16、①②
1、C 2、A 3、D 4、C 5、A 6、B 7、D 8、D 9、C 10、B
26、已知,如图,抛物线y=ax2+bx+c(a≠0)经过x轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,- ),⊙P的圆心P在y轴上,且经过B、C两点,若b=
),⊙P的圆心P在y轴上,且经过B、C两点,若b= ,AB=2
,AB=2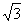 。
。
(1)求抛物线的对称轴及其中C的值。
(2)求抛物线的解析式。
(3)直线BP与⊙P交于另一点D,求证D点在抛物线对称轴上,并求过点D⊙P的切线的解析式。
 犍为县2009级毕业调考数学试题参考答案及评分意见
犍为县2009级毕业调考数学试题参考答案及评分意见
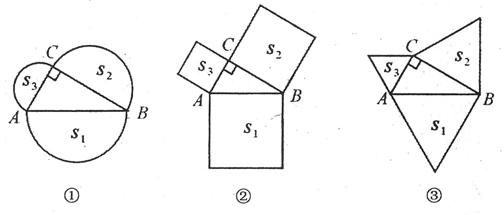
25、如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难证明S1=S2+S3.
(1)如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3有什么关系?(不必证明)
(2)如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3之间的关系并加以证明。
(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1、S2、S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件?证明你的结论。
(4)类比(1)、(2)、(3)的结论,请你总结出一个更具一般意义的结论。
24、如图,⊙0是△ABC的外接圆,且AB=AC,点D在劣弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连接AD、BD。
(1)求证:∠ADB=∠E.
(2)当D点运动到什么位置时,DE是⊙O的切线?说明理由.
(3)当AB=5,BC=6时,求⊙O的半径。

23、关于X的一元二次方程x2+(2m-1)x+m2=0有两根为x1,x2。
(1)求m的取值范围。
(2)当X12-X22=0时,求m的值。
22、如图,某学习小组为了测量河对岸AB的高度,在塔底部B的正对岸点C处,测得仰角∠ACB=30°.
(1)若河宽BC=60米,求塔AB的高。
 (2)若河宽BC的长度元法度量,如何没量塔AB的高度呢?小明想出了另一种方法:从点C出发,沿河岸CD的方向(点B、C、D在同一平面内,且CD⊥BC)走a米,到达D处,测得∠BDC=60°,这样就可以求得塔AB的高度了,请你用这种方法求出塔AB的高,(用含a的代数式表示)
(2)若河宽BC的长度元法度量,如何没量塔AB的高度呢?小明想出了另一种方法:从点C出发,沿河岸CD的方向(点B、C、D在同一平面内,且CD⊥BC)走a米,到达D处,测得∠BDC=60°,这样就可以求得塔AB的高度了,请你用这种方法求出塔AB的高,(用含a的代数式表示)
21、如图,一次函数y=kx+b的图象经过点A(-1,0)和点(1,4)交y轴于点B。
(1)求一次函数解析式和B点坐标。
(2)过B点的另一直线1与直线AB垂直,且交X轴正半轴于点P,求点P的坐标。
(3)点M(0,a)为y轴正半轴上的动点,点N(b,O)为X轴正半轴上的动点,当直线
MN⊥直线AB时,求a:b的值。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com