
8.(2009福建卷文)若双曲线 的离心率为2,则
的离心率为2,则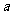 等于
等于
A. 2
B. 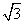


C. 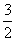 D.
1
D.
1
解析解析 由 ,解得a=1或a=3,参照选项知而应选D.
,解得a=1或a=3,参照选项知而应选D.
7.(2009宁夏海南卷文)已知圆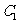 :
: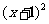 +
+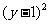 =1,圆
=1,圆 与圆
与圆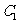 关于直线
关于直线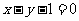 对称,则圆
对称,则圆 的方程为
的方程为
(A)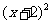 +
+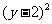 =1
(B)
=1
(B)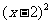 +
+ =1
=1
(C)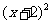 +
+ =1
(D)
=1
(D)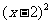 +
+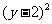 =1
=1
[答案]B
[解析]设圆 的圆心为(a,b),则依题意,有
的圆心为(a,b),则依题意,有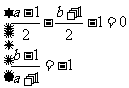 ,解得:
,解得: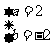 ,对称圆的半径不变,为1,故选B。.
,对称圆的半径不变,为1,故选B。.
6.(2009辽宁卷文)已知圆C与直线x-y=0 及x-y-4=0都相切,圆心在直线x+y=0上,则圆C的方程为
(A)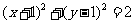 (B)
(B) 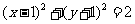
(C)
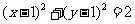 (D)
(D) 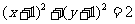
[解析]圆心在x+y=0上,排除C、D,再结合图象,或者验证A、B中圆心到两直线的距离等于半径即可.
[答案]B
5.(2009天津卷文)设双曲线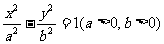 的虚轴长为2,焦距为
的虚轴长为2,焦距为 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A 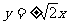 B
B 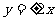 C
C 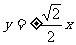 D
D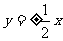
[答案]C
[解析]由已知得到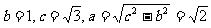 ,因为双曲线的焦点在x轴上,故渐近线方程为
,因为双曲线的焦点在x轴上,故渐近线方程为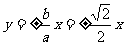
[考点定位]本试题主要考查了双曲线的几何性质和运用。考察了同学们的运算能力和推理能力。
4.(2009安徽卷文)直线 过点(-1,2)且与直线垂直,则
过点(-1,2)且与直线垂直,则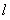 的方程是
的方程是
A.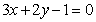 B.
B.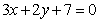
C. 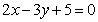 D.
D.
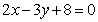
[解析]可得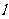 斜率为
斜率为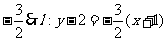 即
即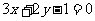 ,选A。
,选A。
[答案]A
3.(2009安徽卷文)下列曲线中离心率为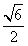 的是21世纪教育网
的是21世纪教育网 

A. B.
B.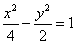 C.
C.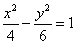 D.
D.
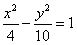
[解析]依据双曲线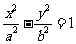 的离心率
的离心率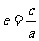 可判断得.
可判断得.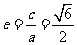 .选B。
.选B。
[答案]B
2.(2009山东卷文)设斜率为2的直线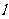 过抛物线
过抛物线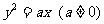 的焦点F,且和
的焦点F,且和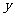 轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).
轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ). 

A.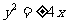 B.
B.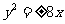 C.
C. 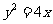 D.
D. 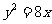
[解析]: 抛物线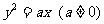 的焦点F坐标为
的焦点F坐标为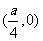 ,则直线
,则直线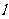 的方程为
的方程为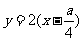 ,它与
,它与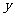 轴的交点为A
轴的交点为A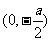 ,所以△OAF的面积为
,所以△OAF的面积为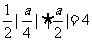 ,解得
,解得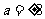 .所以抛物线方程为
.所以抛物线方程为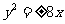 ,故选B.
,故选B. 

答案:B.
[命题立意]:本题考查了抛物线的标准方程和焦点坐标以及直线的点斜式方程和三角形面积的计算.考查数形结合的数学思想,其中还隐含着分类讨论的思想,因参数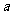 的符号不定而引发的抛物线开口方向的不定以及焦点位置的相应变化有两种情况,这里加绝对值号可以做到合二为一.
的符号不定而引发的抛物线开口方向的不定以及焦点位置的相应变化有两种情况,这里加绝对值号可以做到合二为一.
1.(2009浙江文)已知椭圆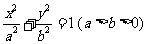 的左焦点为
的左焦点为 ,右顶点为
,右顶点为 ,点
,点 在椭圆上,且
在椭圆上,且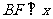 轴, 直线
轴, 直线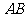 交
交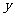 轴于点
轴于点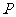 .若
.若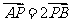 ,则椭圆的离心率是( )21世纪教育网
,则椭圆的离心率是( )21世纪教育网 

A.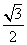 B.
B.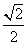 C.
C. D.
D.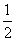
答案:D [命题意图]对于对解析几何中与平面向量结合的考查,既体现了几何与向量的交汇,也体现了数形结合的巧妙应用.
[解析]对于椭圆,因为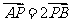 ,则
,则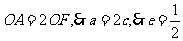 21世纪教育网
21世纪教育网 

10、D (A、火亘xuǎn;B、见jiàn;C、葸xǐ)
9、A(B、蔓wàn;C、瞠chēng;D、间jiān)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com