
2.已知函数f(x)=x4-4x3+10x2,则方程f(x)=0在区间[1,2]上的根有
A.3个 B.2个 C.1个 D.0个
3.导数是研究函数问题的工具,注意它在其它数学问题中的综合与应用。
同步练习 11.5 导数的综合应用
[选择题]
1某物体作s=2(1-t)2的直线运动,则t=0.8 s时的瞬时速度为 ( )
A.4 B.-4 C-4.8 D-0.8
2.利用导数证明不等式有两种方法:
1.利用导数求解不等式问题的核心是利用导数判定函数的单调性,这就转化为一般的函数问题;
由= +得M的坐标为(x,y), 由x0,y0满足C的方程,得点M的轨迹方程为:
+ =1 (x>1,y>2)
(Ⅱ)| |2= x2+y2, y2= =4+ ,
∴| |2=
x2-1++5≥4+5=9 且当x2-1= ,即x=>1时,上式取等号
且当x2-1= ,即x=>1时,上式取等号
故||的最小值为3
[研讨欣赏](2006湖北) 设x=3是函数f(x)=(x2+ax+b)e3-x(x∈R)的一个极值点.
(1)求a与b的关系式(用a表示b),并求f(x)的单调区间;
(2)设 >0,
>0, =(
=(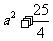 )
) .若存在
.若存在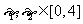 使得|
使得|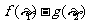 |<1成立,求
|<1成立,求 的取值范围.
的取值范围.
解:(1)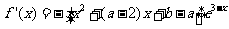
由f′(3)=0得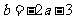
所以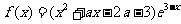

令f′(x)=0得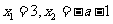
由于x=3是f(x)的极值点,故x1≠x2,即a≠-4
当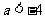 时,
时,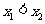 ,故f(x)在
,故f(x)在 上为减函数,在
上为减函数,在 上为减函数,在
上为减函数,在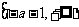 上为增函数
上为增函数
当a>4时,x1>x2,故f (x)在(-∞,-a-1]上为减函数,在[-a-1,3]上为增函数,在[3,+∞)上为减函数.
(2)当a>0时,-a-1<0,故f(x)在[0,3]上为增函数,在[3,4]上为减函数,在[3,+∞)上为减函数
因此f(x)在[0,4]上的值域为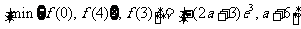
而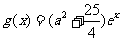 在[0,4]上为增函数,所以值域为
在[0,4]上为增函数,所以值域为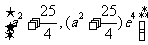
注意到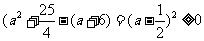 ,
,
故由假设知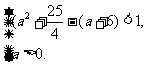 解得
解得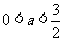
故 的取值范围是
的取值范围是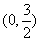
考查知识:函数、不等式和导数的应用知识,考查综合运用数学知识解决问题的能力.
[例1]证明:当x>0时,有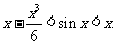
证明:设f(x)=x-sinx,于是f(0)=0.
∵f/(x)=1-cosx(仅在x=2kπ(k∈Z)处f/(x)=0
∴当x>0时,f(x)单调递增,从而有f(x)>f(0)
即x-sinx>0, x>sinx(x>0)
为证不等式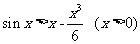 ,设
,设
g(x)=sinx-x+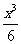 ,则g(0)=0,
,则g(0)=0,
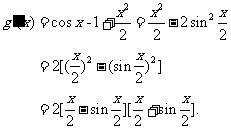
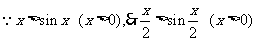
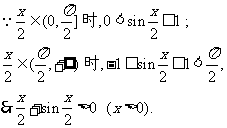
于是g/(x)>0,∴g(x)在x>0时递增,从而有g(x)>g(0)=0
即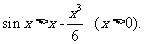
故当x>0时有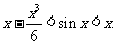
提炼方法:证不等式的依据I:
(1) 若函数f(x)在x>a可导,且递增,则f(x)>f(a);
(2) 若函数f(x)在x>a可导,且递减,则f(x)《f(a);
关键在于构造恰当的函数,一般是左-右,右-左,左÷右等。
[例2]已知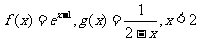
求证:函数f(x)图像上的点不可能在函数g(x)图像的上方。
证明:设F(x)=(2-x)ex-1,(x<2)
∵F/(x)=(1-x)ex-1,
当x<1时,F/(x)>0,当1<x<2时,F/(x)<0.
∴x=1时,F(x)有极大值,也就是最大值。
∴F(x)≤F(1)=1,又x<2,
∴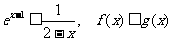
∴函数f(x)图像上的点不可能在函数g(x)图像的上方。
提炼方法:证不等式的依据II:
(1)若函数f(x)在某一范围内有最小值m,则f(x)≥m.
(2)若函数f(x)在某一范围内有最大值M,则f(x)≤m.
[例3](2006全国Ⅰ)已知函数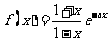
(Ⅰ)设a>0,讨论y=f(x)的单调性;
(Ⅱ)若对任意x∈(0,1)恒有f(x)>1,求a的取值范围
解(Ⅰ)f(x)的定义域为(-∞,1)∪(1,+∞)。 对f(x)求导数得 f '(x)= e-ax
(ⅰ)当a=2时, f '(x)= e-2x, f '(x)在(-∞,0), (0,1)和(1,+ ∞)均大于0, 所以f(x)在(-∞,1), (1,+∞) 为增函数;
(ⅱ)当0<a<2时, f '(x)>0, f(x)在(-∞,1), (1,+∞)为增函数;
(ⅲ)当a>2时, 0<<1, 令f '(x)=0 ,解得x1= - 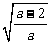 , x2=
, x2= 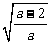
当x变化时, f '(x)和f(x)的变化情况如下表:
|
x |
(-∞, -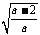 ) ) |
(-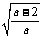 , ,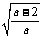 ) ) |
(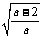 ,1) ,1) |
(1,+∞) |
|
f '(x) |
+ |
- |
+ |
+ |
|
f(x) |
↗ |
↘ |
↗ |
↗ |
f(x)在(-∞, -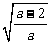 ), (
), (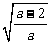 ,1), (1,+∞)为增函数, f(x)在(-
,1), (1,+∞)为增函数, f(x)在(-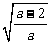 ,
,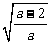 )为减函数。
)为减函数。
(Ⅱ)(ⅰ)当0<a≤2时, 由(Ⅰ)知: 对任意x∈(0,1)恒有f(x)>f(0)=1
(ⅱ)当a>2时, 取x0= 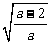 ∈(0,1),则由(Ⅰ)知 f(x0)<f(0)=1
∈(0,1),则由(Ⅰ)知 f(x0)<f(0)=1
(ⅲ)当a≤0时, 对任意x∈(0,1),恒有 >1且e-ax≥1,得
f(x)= e-ax≥ >1 综上当且仅当a∈(-∞,2]时,对任意x∈(0,1)恒有f(x)>1 。
综上当且仅当a∈(-∞,2]时,对任意x∈(0,1)恒有f(x)>1 。
特别提示:对于求单调区间、极值、最值问题,根据导数的零点把定义区间分开,列出表格,再分析各区间导数的符号,进而确定单调区间、极值最值,清楚直观不易出错。
[例4] (2006全国Ⅰ) 在平面直角坐标系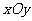 中,有一个以
中,有一个以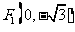 和
和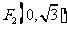 为焦点、离心率为
为焦点、离心率为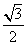 的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与
的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与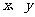 轴的交点分别为A、B,且向量
轴的交点分别为A、B,且向量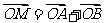
 求:
求:
(Ⅰ)点M的轨迹方程;
(Ⅱ)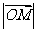 的最小值。
的最小值。
解: 椭圆方程可写为: + =1 式中a>b>0 , 且 得a2=4,b2=1,所以曲线C的方程为: x2+ =1 (x>0,y>0) y=2(0<x<1) y '=-
y=2(0<x<1) y '=-
设P(x0,y0),因P在C上,有0<x0<1, y0=2, y '|x=x0= - ,得切线AB的方程为:
6.设f(x)=x3-3x+c,则 (x)=3x2-3=3(x2-1).
(x)=3x2-3=3(x2-1).
当x∈(0,1)时, (x)<0恒成立.
(x)<0恒成立.
∴f(x)在(0,1)上单调递减.
∴f(x)的图象与x轴最多有一个交点.
因此方程x3-3x+c=0在[0,1)上至多有一实根.
5. y′=-4x2+b,若y′值有正、有负,则b>0.答案:b>0
6.方程x3-3x+c=0在[0,1]上至多有_______个实数根.
简答:1-4.DBDC;
5.若函数y=-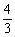 x3+bx有三个单调区间,则b的取值范围是________.
x3+bx有三个单调区间,则b的取值范围是________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com