19. 如图，在棱长为1的正方体中，AP=BQ=b(0<b<1)，截面PQEF∥，截面PQGH∥．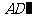

(Ⅰ)证明：平面PQEF和平面PQGH互相垂直；

(Ⅱ)证明：截面PQEF和截面PQGH面积之和是定值，

并求出这个值；

(Ⅲ)若，求与平面PQEF所成角的正弦值．

18. 甲、乙、丙3人投篮,投进的概率分别是,　 , .现3人各投篮1次,求:

(Ⅰ)3人都投进的概率;

(Ⅱ)3人中恰有2人投进的概率.

17.设锐角三角形的内角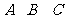的对边分别为，．

(Ⅰ)求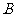的大小；

(Ⅱ)求的取值范围．

19. 如图，已知点P在正方体ABCD－A₁B₁C₁D₁的对角线BD₁上，∠PDA=60°。

(1)求DP与CC₁所成角的大小；

(2)求DP与平面AA₁D₁D所成角的大小。

18. 盒中装着标有数字1，2，3，4的卡片各2张，从盒中任意任取3张，每张卡片被抽出的可能性都相等，求：

(Ⅰ)抽出的3张卡片上最大的数字是4的概率；

(Ⅱ)抽出的3张中有2张卡片上的数字是3的概念；

(Ⅲ)抽出的3张卡片上的数字互不相同的概率.

17. 设函数f(x)=a·b，其中向量a=(2cosx，1)，b=(cosx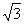， sin2x)，x∈R.

(Ⅰ)若f(x)=1－且x∈[－，]，求x；

(Ⅱ)若函数y=2sin2x的图象按向量c=(m，n)(|m|<)平移后得到函数y=f(x)的图象，求实数m、n的值.

19. 如图，在四棱锥中，侧面PAD⊥底面ABCD,侧棱PA=PD=,底面ABCD为直角梯形，其中BC∥AD,AB⊥CD,AD=2AB=2BC=2,O为AD中点。

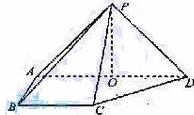(1)求证：PO⊥平面ABCD;

(2)求异面直线PB与CD所成角的余弦值；

(3)求点A到平面PCD的距离

18. 某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意出取2件产品进行检验。设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品。

(I)求取6件产品中有1件产品是二等品的概率。

(II)若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品被用户拒绝的概率。

17.已知函数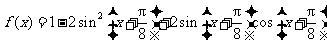．求：

(I)函数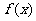的最小正周期；

(II)函数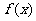的单调增区间．

19. 如图，在四棱锥中，底面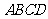四边长为1的菱形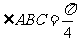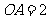，, , ,为的中点，为的中点。

(Ⅰ)证明：直线；

(Ⅱ)求异面直线AB与MD所成角的大小；

(Ⅲ)求点B到平面OCD的距离。