
实验原理:DNA遇甲基绿呈绿色,RNA可被吡罗红染成红色
 实验步骤
实验步骤
|
步骤 |
器材与试剂 |
 作用与原理 作用与原理 |
|
(1)制片 |
①将牙签刮下的口腔上皮细胞置于载玻片上0.9%的NaCl溶液滴 ②载玻片烘干 |
1 0.9%的NaCl溶液防止细胞破裂,2 维持细胞形态。 3 烘干使细胞固定在载玻片上 |
|
(2)水解 |
8%HCl中30℃保温5分钟 |
盐酸能改变细胞膜的通透性,加速染色剂进入细胞,同时使染色体中的DNA与蛋白质分离。 |
|
(3)冲洗 |
用蒸馏水缓流冲洗10分钟 |
|
|
(4)染色 |
2滴吡罗红甲基绿染色5分钟 |
甲基绿使DNA染上绿色 吡罗红使RNA染上红色 |
|
(5)观察 |
显微镜下观察 |
|
实验结果: 细胞核呈绿色,细胞质呈红色.
分布:真核生物的DNA主要分布在细胞核中,线粒体和叶绿体内也含有少量的DNA;RNA主要分布在细胞质中。
|
2、考点解读:
|
内容 |
说明 |
|
(1)教材中有关的实验原理、方法和技能 (2)教材实验的外延和拓展,运用所学方法技能设计简单实验 (3)设计实验 考察实验思路,实验设计的合理程序及其严密性。 培养以及学生对实验的评价能力。 |
实验是培养学生能力的有效手段,也是区分学生成绩的方法,实验,尤其是实验设计是很多学生的软肋。 |
生物实验一是高考每年的必考内容,从近几年高考实验题题型变化来看,借助实验方法创设新情境,越来越侧重于考查学生的实验思维能力,主要考查学生理解实验原理的情况、分析实验结果的能力和灵活运用实验知识的能力,考察不同情境下迁移知识的能力。近几年的高考理综测试题中,生物实验部分有比较固定的模式:一般第二卷有一道大的实验题,主要包括观察实验、分析实验和设计实验等形式。第一卷叶占有一定的分值。与实验有关的试题一般在30分左右。
针对高考形式和近几年的情况,我们应该:
⑴对于教材要求完成实验中的有些内容尤其是实验原理、方法和技能等,要求学生准确记住,比如颜色反应,叶绿体中色素分离和提取的试剂等等。培养学生的动手能力,比如有丝分裂林时装片的制作等实验。
⑵通过实验课的学习,不但可以独立完成课本上的实验,还应该有举一反三的能力,并运用自己学到的知识和技能设计简单的实验,并且说出设计原理和方法,评价自己的实验。也就是说,考生要能从所学的实验中提炼、归纳可以应用到生活的知识。,如建立模型进行研究的方法等,并能迁移到新的情境中,运用其解决问题。这类要求不但要求学生能够设计实验的思想,比如要验证甲状腺激素的作用。如果只是会实验方法,可以设计实验,而不懂得甲状腺激素的作用 ,那么设计出来也不会太完美,这类实验往往依托于教材已知的实验,是课本实验的拓展和外延,
⑶新课标要求培养学生探究能力,一般步骤包括作出观察现象→作出假设→设计实验→进行实验→结果和结论,进行交流的能力,从近几年的高考来看,考生往往在这部分失分较多,这部分内容考察学生的综合分析能力,设计方案,归纳总结能力等方面的能力,考察比较广泛,在平时应该多注意培养。
|
|
|
 二、知识网络
二、知识网络
(主要实验)
|

1、考点盘点
14.已知矩阵M有特征值 1=4及对应的一个特征向量e1=
1=4及对应的一个特征向量e1=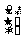 ,并有特征值
,并有特征值 2=-1及对应的一个特征向量e2=
2=-1及对应的一个特征向量e2=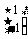 .
.
(1)求矩阵M;(2)求M2 008e2.
解 (1)设M=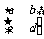 ,
,
则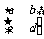
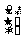 =4
=4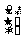 =
=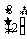 ,
,
故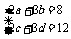 .
.
又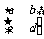
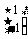 =(-1)
=(-1)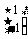 =
=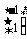 ,
,
故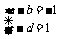 .
.
联立以上两个方程组,
解得a=1,b=2,c=3,d=2,故M=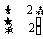 .
.
(2)M2 008e2=
 e2=(-1)2
008
e2=(-1)2
008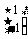 =
=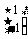 .
.
13.已知矩阵A= ,求特征值及特征向量.
,求特征值及特征向量.
解 矩阵A的特征多项式为f( )=
)=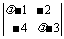 .
.
令f( )=0,即
)=0,即 2-4
2-4 -5=0,得
-5=0,得 1=-1,
1=-1,  2=5,
2=5,
所以矩阵A的特征值为 1=-1,
1=-1,  2=5.
2=5.
将 1=-1代入二元一次方程组
1=-1代入二元一次方程组
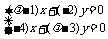 .
①
.
①
即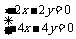 ,得x=y,它有无穷多个非零解
,得x=y,它有无穷多个非零解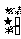 ,
,
其中x≠0,故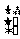 为矩阵属于特征值
为矩阵属于特征值 =-1的特征向量.
=-1的特征向量.
同样,将 1=5代入二元一次方程组①,
1=5代入二元一次方程组①,
则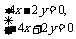 得y=2x,
得y=2x,
它有无穷多个非零解 ,其中x≠0,
,其中x≠0,
故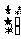 为矩阵属于特征值
为矩阵属于特征值 =5的特征向量.
=5的特征向量.
12.(2008·江苏)在平面直角坐标系xOy中,设椭圆4x2+y2=1在矩阵A= 对应的变换下得到曲线F,求F的方程.
对应的变换下得到曲线F,求F的方程.
解 设P(x0,y0)是椭圆上任意一点,点P(x0,y0)在矩阵A对应的变换下变为点P′( ,
, ),则有
),则有
 =
=
 ,即
,即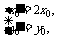 所以
所以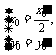
又因为点P在椭圆上,故4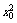 +
+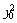 =1,
=1,
从而( )2+(
)2+( )2=1.
)2=1.
所以曲线F的方程为x2+y2=1.
11.(2008·如东质检)已知矩阵A= ,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3).
,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3).
(1)求实数a的值;
(2)求矩阵A的特征值及特征向量.
解(1)由
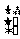 =
=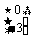
得a+1=-3 a=-4.
a=-4.
(2)由(1)知A=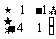
则矩阵A的特征多项式为
f( )=
)=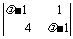 =(
=( -1)2-4=
-1)2-4= 2-2
2-2 -3
-3
令f( )=0,得矩阵A的特征值为-1或3.
)=0,得矩阵A的特征值为-1或3.
设矩阵A的特征向量为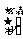
当 =-1时,
=-1时,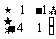
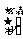 =(-1)
=(-1) 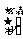
即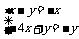 ,所以y=2x.
,所以y=2x.
∴矩阵A的属于特征值-1的一个特征向量为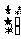 .
.
当 =3时,
=3时,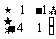
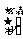 =3
=3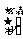 ,
,
即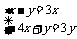 ,所以2x+y=0.
,所以2x+y=0.
∴矩阵A的属于特征值3的一个特征向量为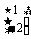 .
.
10.已知二阶矩阵M有特征值 =8及对应的一个特征向量e1=
=8及对应的一个特征向量e1=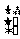 ,并且矩阵M对应的变换将点(-1,2)变换成(-2,4).
,并且矩阵M对应的变换将点(-1,2)变换成(-2,4).
求直线l:x-y+1=0在矩阵M的变换下的直线l′的方程.
解 设M=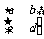 ,则
,则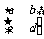
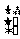 =8
=8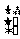 =
= ,
,
故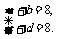
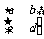
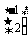 =
=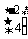 ,
,
故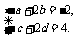
联立以上两方程组解得a=6,b=2,c=4,d=4,
故M= .
.
设点(x,y)是直线l上的任一点,其在矩阵M的变换下对应的点的坐标为(x′,y′),
则 =
=
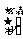 =
=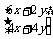 ,
,
即x=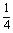 x′-
x′-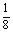 y′,y=-
y′,y=-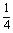 x′+
x′+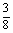 y′,
y′,
代入直线l的方程后并化简得x′-y′+2=0,
即x-y+2=0.
所以变换后的直线方程为x-y+2=0.
9.试求曲线y=sinx在矩阵MN变换下的函数解析式,其中M=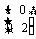 ,N=
,N= .
.
解 MN=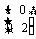
 =
= ,
,
即在矩阵MN变换下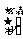 →
→ =
=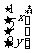 ,
,
则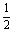 y′=sin2x′,即曲线y=sinx在矩阵MN变换下的函数解析式为y=2sin2x.
y′=sin2x′,即曲线y=sinx在矩阵MN变换下的函数解析式为y=2sin2x.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com