2．下列各句中加点成语的使用恰当的一项是

(　)

A．秋天到了，行将就木的落叶任秋风卷起，到处飘零，而连绵的秋雨不停地下着，这一切勾起了游子们绵绵的乡愁。

B．反对克隆技术的人的一个重要理由，是害怕克隆出“本·拉登”式的人物，其实这只是杯弓蛇影。

C．当你养尊处优、春风得意的时候，一定要居安思危，决不能丧失忧患意识。

D．当年，飓风“卡特里娜”横扫了美国密西西比州的不少地区，并给该州带来了迄今为止最惨重的洪水灾害，致使生灵涂炭，不少难民流离失所。

[解析]　A项“行将就木”指人将要死去，不能用于形容落叶。B项“杯弓蛇影”，看见酒杯中所映现的弓的影子而误以为酒杯里有蛇，比喻因疑神疑鬼而妄自惊慌。在这里应用“杞人忧天”。D项“生灵涂炭”形容政治混乱时期人民处在极端困苦的环境中。用错对象。

[答案]　C

1．下列句子中加点的成语，使用正确的一项是

(　)

A．最近一段时间，在巴基斯坦发生的一系列耸人听闻的恐怖事件，再次给这个饱受社会动乱之苦的国家敲响了警钟。

B．面对一位谦谦君子，我不会展露本性，因为我看不清他温和文雅的外衣下藏着颗怎样的本心。君子是个面具，是一具没有生命的躯壳，至少我是这样认为的。

C．我国许多城市都建立了食品质量报告制度，定期向社会公布有关部门的检验结果，从而使那些劣质食品在劫难逃。

D．菏泽牡丹属中原牡丹种群，花色五花八门，花型千变万化。其主要花色为粉、红(含紫红)、紫、蓝、黄、白、黑、绿、复色九大色系。

[解析]　B项“谦谦君子”指谦虚谨慎，能够严格要求自己、品格高尚的人。A项“耸人听闻”指故意言过其实，夸大其辞，使人听了感到震惊。应改为“骇人听闻”。属不理解成语含义用错。C项“在劫难逃”，迷信地认为命中注定要遭受灾祸，想逃是逃不了的，现指灾祸不可避免，语境不合。D项“五花八门”比喻花样多端，种类繁多。此处用“丰富多彩”比较妥当。

[答案]　B

12.若直线y＝2a与函数y＝|a^x－1|(a＞0且a≠1)的图象有两个公共点，求a的取值范围.

解：当0＜a＜1时，y＝|a^x－1|的图象如右图所示，

由已知得0＜2a＜1，∴0＜a＜.

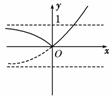当a＞1时，y＝|a^x－1|的图象如右图所示.

由题意可得：0＜2a＜1，

∴0＜a＜，与a＞1矛盾.

综上可知：0＜a＜.

11.函数f(x)的图象是如图所示的折线段OAB，其中点A(1,2)、B(3,0)，函数g(x)＝(x－1)f(x)，则函数g(x)的最大值为　　.

解析：依题意得f(x)

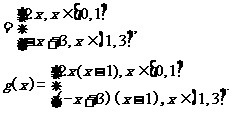
当x∈[0,1]时，g(x)＝2x(x－1)＝2x²－2x＝2(x－)²－的最大值是0；

当x∈(1,3]时，g(x)＝(－x+3)(x－1)＝－x²+4x－3＝－(x－2)²+1的最大值是1.

因此，函数g(x)的最大值为1.

答案：1

10.(文)使log₂(－x)＜x+1成立的x的取值范围是　　　　　　　　　　　　　　 (　)

A.(－1,0)　　B.[－1,0)　　　 C.(－2,0)　　D.[－2,0)

解析：作出y＝log₂(－x)，y＝x+1的图象，知满足条件的x∈(－1,0).

答案：A

(理)(2010·平顶山模拟)f(x)的定义域为R，且f(x)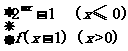＝若方程f(x)＝x+a有两不同实根，则a的取值范围为　　　　　　　　　　　　　　　　　　 (　)

A.(－∞，1) 　　　　　　　　　　　　　B.(－∞，1]

C.(0,1)　 　　　　　　　　　　　　　　　D.(－∞，+∞)

解析：x≤0时，f(x)＝2^－x－1，

1＜x≤2时，0＜x－1≤1，f(x)＝f(x－1).

故x＞0时，f(x)是周期函数，如图，

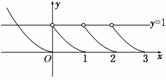
欲使方程f(x)＝x+a有两解，即函数f(x)的图象与直线y＝x+a有两个不同交点，故a＜1，则a的取值范围是(－∞，1).

答案：A

9.(2010·东北师大附中模拟)函数y＝f(x)的图象是圆心在原点的单位圆的两段弧(如图)，则不等式f(x)＜f(－x)+x的解集为　　　　　　　　　　　　　　　　　　 (　)

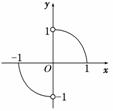
A.{|－＜x＜0或＜x≤1}

B.{x|－1＜x＜－或＜x≤1}

C.{x|－1＜x＜－或0＜x＜}

D.{x|－＜x＜且x≠0}

解析：由图象可知，该函数f(x)为奇函数，故原不等式可等价转化为f(x)＜x，

当x＝1时，f(x)＝0＜，显然成立，

当0＜x＜1时，f(x)＝，

∴1－x²＜x²，∴＜x＜1.

当－1≤x＜0时，－＜x，

∴1－x²＞x²，∴－＜x＜0.

综上所述，不等式f(x)＜f(－x)+x的解集为

{x|－＜x＜0或＜x≤1}.

答案：A

8.函数f(x)＝的图象如图所示，则a+b+c＝　　.

解析：由图象可求得直线的方程为y＝2x+2，又函数y＝log_c(x+)

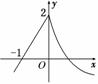的图象过点(0,2)，将其坐标代入可得c＝，

所以a+b+c＝2+2+＝.

答案：

7.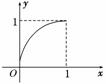已知定义在区间[0,1]上的函数y＝f(x)的图象如图所示，对于满足0＜x₁＜x₂＜1的任意x₁、x₂，给出下列结论：

①f(x₂)－f(x₁)＞x₂－x₁；

②x₂f(x₁)＞x₁f(x₂)；

③＜f ().

其中正确结论的序号是　　(把所有正确结论的序号都填上).

解析：由f(x₂)－f(x₁)＞x₂－x₁，可得＞1，即两点(x₁，f(x₁))与(x₂，f(x₂))连线的斜率大于1，显然①不正确；由x₂f(x₁)＞x₁f(x₂)得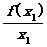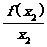＞，即表示两点(x₁，f(x₁))、(x₂，f(x₂))与原点连线的斜率的大小，可以看出结论②正确；结合函数图象，容易判断③的结论是正确的.

答案：②③

6.(2010·包头模拟)已知下列曲线：

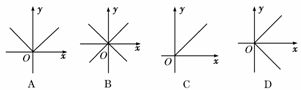
以及编号为①②③④的四个方程：

①－＝0；②|x|－|y|＝0；③x－|y|＝0；④|x|－y＝0.

请按曲线A、B、C、D的顺序，依次写出与之对应的方程的编号　　.

解析：按图象逐个分析，注意x、y的取值范围.

答案：④②①③

5.函数f(x)＝·a^x(a＞1)图象的大致形状是　　　　　　　　　　　　　　　　　 (　)

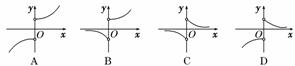
解析：f(x)是分段函数，根据x的正负写出分段函数的解析式，f(x)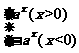＝，∴x＞0时，图象与y＝a^x在第一象限的图象一样，x＜0时，图象与y＝a^x的图象关于x轴对称，故选B.

答案：B