
在函数或数列的极限都是存在的前提下,才能运用极限的运算法则进行计算;当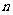 无限增大(或x无限的趋向于某值)时,分式的分子、分母都无限增大,分子、分母都没有极限(分式的分子、分母都趋向于0), 则极限运算法则不能直接运用;无穷等比数列各项的和公式;化循环小数为分数的方法
无限增大(或x无限的趋向于某值)时,分式的分子、分母都无限增大,分子、分母都没有极限(分式的分子、分母都趋向于0), 则极限运算法则不能直接运用;无穷等比数列各项的和公式;化循环小数为分数的方法
5.化循环小数为分数:(1) (2)
(2)
答案:(1)3/11 (2)34/111
4.求下列无穷等比数列各项的和:
(1)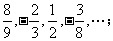 (2)
(2)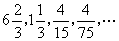
答案:(1)32/63 (2) 5/6
3.求下列极限:(1)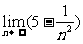 ;
(2)
;
(2)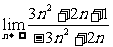 ;
;
解:(1)
(2)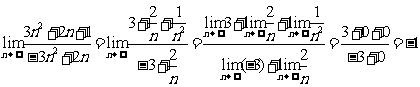 .
.
2. 已知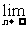 an=2,
an=2,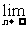 bn=-
bn=-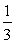 ,求下列极限.
,求下列极限.
(1) 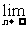 (2an+3bn-1) (2)
(2an+3bn-1) (2)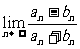
解:(1)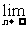 (2an+3bn-1)=
(2an+3bn-1)=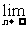 (2an)+
(2an)+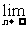 (3bn)-
(3bn)-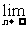 1
1
=2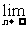 an+3
an+3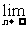 bn-1=2·2+3·(-
bn-1=2·2+3·(-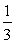 )-1=2.
)-1=2.
(2)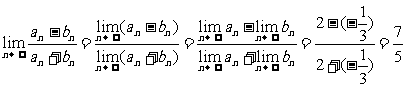
1.求下列极限:
(1)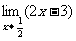 ;(2)
;(2)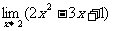 ;(3)
;(3)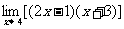 ;
(4)
;
(4)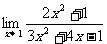 ;(5)
;(5) ;(6)
;(6)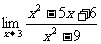 ;
;
(7)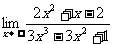 ;(8)
;(8)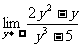

答案:⑴-2 ⑵3 ⑶49 ⑷2/3 ⑸-2 ⑹1/6 ⑺0 ⑻0
(三)公比绝对值小于1的无穷等比数列前n项和的极限
公比的绝对值小于1的无穷等比数列前n项的和,当n无限增大时的极限,叫做这个无穷等比数列各项的和.
设无穷等比数列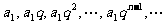 的公比
的公比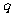 的绝对值小于1,则其各项的和S为
的绝对值小于1,则其各项的和S为 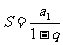
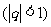
例7 求无穷等比数列0.3, 0.03, 0.003,… 各项的和.
解:0.3, 0.03, 0.003,…的首项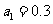 ,公比
,公比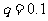
所以 s=0.3+ 0.03+ 0.003+…=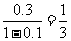
例8 将无限循环小数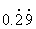 化为分数.
化为分数.
解: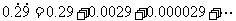
=
(二)先求和再求极限
例6 求下列极限:
(1)  ;(2)
;(2)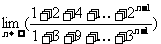
解:(1) 
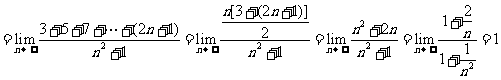 (2)
(2)
(一)运用极限的四则运算法则求数列的极限
例1 求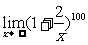 .(利用公式法,
.(利用公式法,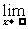 [f(x)]n=[
[f(x)]n=[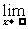 f(x)]n.)
f(x)]n.)
解:
例2 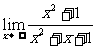 .(利用
.(利用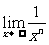 =0)
=0)
解: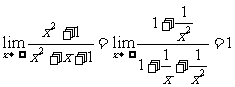
例3 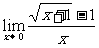 .(分子有理化法.)
.(分子有理化法.)
解: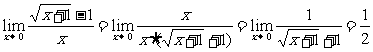
例4 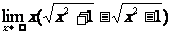 .(分子有理化法)
.(分子有理化法)
解: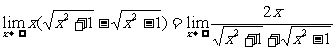
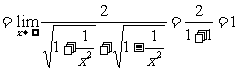
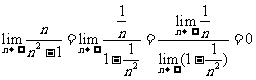
例5 求下列有限:(1)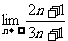 (2)
(2)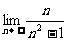
分析:(1)(2)当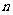 无限增大时,分式的分子、分母都无限增大,分子、分母都没有极限,上面的极限运算法则不能直接运用
无限增大时,分式的分子、分母都无限增大,分子、分母都没有极限,上面的极限运算法则不能直接运用
解:(1)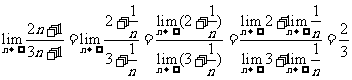
(2)
7. 对于函数极限有如下的运算法则:
如果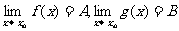 ,那么
,那么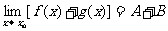 ,
,
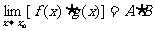 ,
, 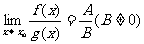

当C是常数,n是正整数时: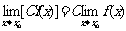 ,
,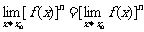
这些法则对于 的情况仍然适用
的情况仍然适用 
8 数列极限的运算法则:
与函数极限的运算法则类似, 如果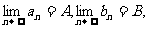 那么
那么
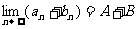
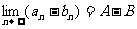
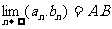
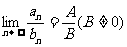

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com