
3.(江西省五校2008届高三开学联考)已知向量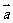 ≠
≠ ,|
,| |=1,对任意t∈R,恒有|
|=1,对任意t∈R,恒有|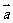 -t
-t |≥|
|≥|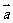 -
- |,则
( )
|,则
( )
A.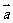 ⊥
⊥ B.
B. ⊥(
⊥(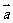 -
- ) C.
) C.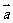 ⊥(
⊥(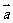 -
- ) D.(
) D.(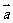 +
+ )⊥(
)⊥(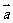 -
- )
)
答案:B
2.(安徽省皖南八校2008届高三第一次联考)已知向量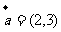 ,
,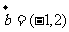 ,若
,若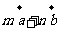 与
与  共线,则
共线,则 等于( )
等于( )
A.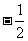 ; B.
; B.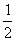 ; C.
; C. ; D.
; D. ;
;
答案 A
1.(江苏省启东中学高三综合测试四)在 中,
中, =a,
=a, =b,M为OB的中点,N为AB的中点,ON,AM交于点P,则
=b,M为OB的中点,N为AB的中点,ON,AM交于点P,则 =
( )
=
( )
A.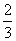 a-
a-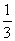 b B.-
b B.-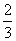 a+
a+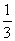 b C.
b C.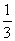 a-
a-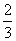 b D.-
b D.-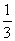 a+
a+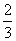 b
b
答案 B
25.(安徽省江南十校2009年高三高考冲刺)在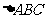 中,
中,
 ,记
,记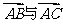 的夹角为
的夹角为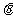 .
.
(Ⅰ)求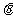 的取值范围;
的取值范围;
(Ⅱ)求函数 的最大值和最小值.
的最大值和最小值.
解 (1)由余弦定理知: ,又
,又 ,
,
所以 ,又
,又 即为
即为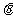 的取值范围;
的取值范围;
(Ⅱ)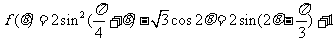 ,因为
,因为
 ,所以
,所以 ,因此
,因此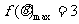 ,
,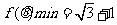 .
. 
2007--2008年联考题
24.(2009年宁波市高三“十校”联考)已知向量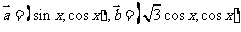 且
且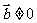 ,函数
,函数
(I)求函数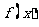 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(II)若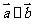 ,分别求
,分别求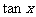 及
及 的值。
的值。
(I)解;

得到的单调递增区间为
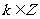
(II)
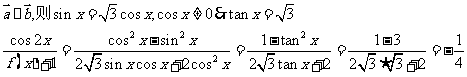
23.(山东日照2009年模拟)已知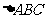 中,角
中,角 的对边分别为
的对边分别为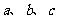 ,且满足
,且满足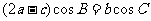 。
。
(I)求角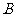 的大小;
的大小;
(Ⅱ)设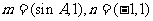 ,求
,求 的最小值。
的最小值。
解 (I)由于弦定理 ,
,
有
代入 得
得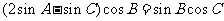 。
。
即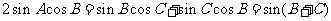 .
.
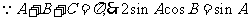



(Ⅱ) ,
,
由 ,得
,得 。
。
所以,当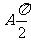 时,
时, 取得最小值为0,
取得最小值为0,
22.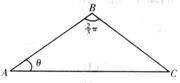 (山东临沂2009年模拟)如图,已知△ABC中,|AC|=1,∠ABC=
(山东临沂2009年模拟)如图,已知△ABC中,|AC|=1,∠ABC= ,∠BAC=θ,记
,∠BAC=θ,记 。
。
(1) 求 关于θ的表达式;
关于θ的表达式;
(2) 求 的值域。
的值域。
解:(1)由正弦定理,得




(2)由 ,得
,得

∴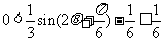 ,即
,即 的值域为
的值域为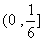 .
.
21.(山东省滨州市2009年模拟)已知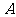 、
、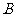 、
、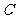 分别为
分别为 的三边
的三边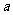 、
、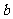 、
、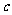 所对的角,向量
所对的角,向量 ,
,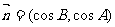 ,且
,且 .
.
(Ⅰ)求角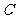 的大小;
的大小;
(Ⅱ)若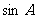 ,
, ,
, 成等差数列,且
成等差数列,且 ,求边
,求边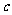 的长.
的长.
解 (Ⅰ)
在 中,由于
中,由于 ,
,
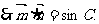
又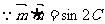 ,
,

又 ,所以
,所以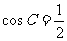 ,而
,而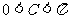 ,因此
,因此 .
.
(Ⅱ)由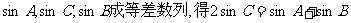 ,
,
由正弦定理得
 ,
,
即 ,由(Ⅰ)知
,由(Ⅰ)知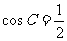 ,所以
,所以
由余弦弦定理得 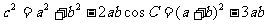 ,
,
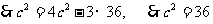 ,
,
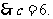
20.(2009广东江门模拟)如图4,已知点 和
和
单位圆上半部分上的动点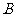 .
.
⑴若 ,求向量
,求向量 ;
;
⑵求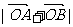 的最大值.
的最大值.
解 依题意, ,
, (不含1个或2个端点也对)
(不含1个或2个端点也对)
 ,
,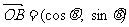 (写出1个即可)---------3分
(写出1个即可)---------3分
因为 ,所以
,所以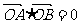 ---------4分,即
---------4分,即 -
-
解得 ,所以
,所以 .
.
⑵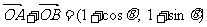 ,
,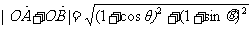
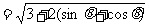 ------11分
------11分  ------12分
------12分
当 时,
时,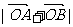 取得最大值,
取得最大值,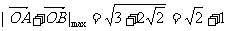 .
.
19.(黄山市2009届高中毕业班第一次质量检测)已知△ABC的面积S满足

(1)求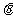 的取值范围;
的取值范围;
(2)求函数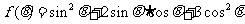 的最大值
的最大值
解 (1)由题意知 .
.

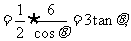
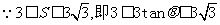 ,
,

(2)
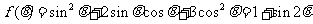



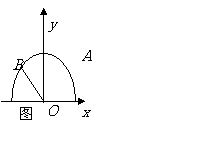
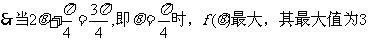 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com