
4.已知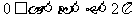 ,
,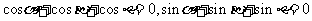 ,求
,求 。
。
3.化简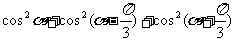 。
。
2.若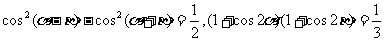 ,求
,求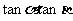 。
。
1.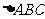 中,
中,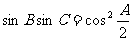 ,试判断
,试判断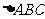 的形状。
的形状。
3.不仅要熟练掌握基本公式,更要做到思路开阔,善于选择适当的公式进行变换。对于有条件的求值、化简、证明问题,关键是找出条件与结论之间角、函数名称等之间的差异及联系。
2.三角变换主要有变名、变角与变形三种,如利用两角和与差的三角函数、二倍角公式、降幂公式等。
1.熟记以下公式:
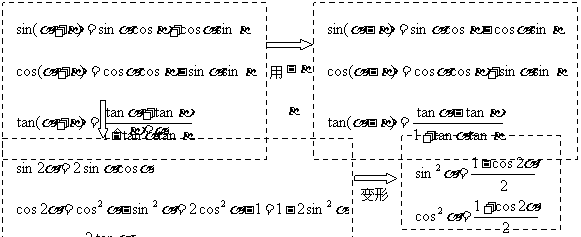
你能在空白纸上独立地默写一遍吗?你还记得万能代换公式和其他常用结论吗?与你的同桌比一比,看谁写得多?
10. 求证:在非Rt△ABC中,若a>b,ha、hb分别表示a、b边上的高,则必有a+ha>b+hb.
证明:设S表示△ABC的面积,则
S=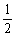 aha=
aha=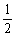 bhb=
bhb=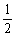 absinC.
absinC.
∴ha=bsinC,hb=asinC.
∴(a+ha)-(b+hb)=a+bsinC-b-asinC
=(a-b)(1-sinC).
∵C≠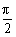 ,∴1-sinC>0.
,∴1-sinC>0.
∴(a-b)(1-sinC)>0.
∴a+ha>b+hb.
[探索题]已知x,y,z∈(0,1)且x+y+z=2,记u=xy+yz+zx,求证: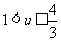
证明:3u=xy+yz+zx+2xy+2yz+2zx

=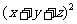 =4,故
=4,故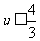 。又
。又
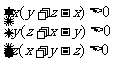 三式相加得
三式相加得
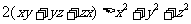 ,两边加上
,两边加上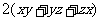 得
得
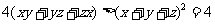
∴ u>1,原不等式得证。
9. 设x>0,y>0且x≠y,求证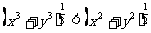
证明:由x>0,y>0且x≠y,要证明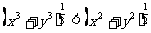
只需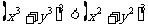 即
即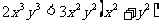
只需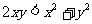
由条件,显然成立.∴原不等式成立
8.己知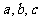 都是正数,且
都是正数,且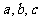 成等比数列,
成等比数列,
求证: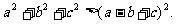
证明: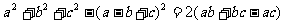

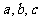 成等比数列,
成等比数列,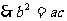

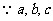 都是正数,
都是正数,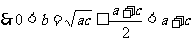


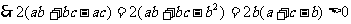

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com