
4.电功率与热功率之间的关系
纯电阻电路中,电功率等于热功率,非纯电阻电路中,电功率只有一部分转化成热功率.
纯电阻电路:电路中只有电阻元件,如电熨斗、电炉子等.
非纯电阻电路:电机、电风扇、电解槽等,其特点是电能只有一部分转化成内能.
[例4]一只标有“220 V,60 W”字样的灯泡,在额定电压下工作时,灯丝中通过的电流多大?如果线路电压下降到200V时,它的功率多大?(假设灯丝电阻不随温度而变化)
解析:灯泡上标有“220 V,60 W”的字样,表明灯泡的额定电压(即正常一作的电压)为 220 V,只有在这个电压下,它的功率才是额定功率60w.如果实际的电压不是220V,那么它的功率就不再是60 W.由题意可认为它相当于一个阻值不变的电阻.
灯泡的工作电流I=P/U=60/220=0。27(A) 灯泡的电阻R=U2/P=2202/60=807(Ω)
灯泡的实际功率 P/=U/2/R=2002/807= 50(W)
点评:由公式P=U2/R可知,当用电器电阻R不变时,P∝U2,可用P1/P2=U12/U22来计算,这样就不必算出灯丝的电阻.用电器实际功率的大小,是由加在用电器两端的实际电压的大小决定的.
[例5]直流电动机线圈的电阻为R,当电动机工作时通过线圈的电流是I,此时它两端的电压为U,则电动机的输出功率为( )
A.UI;B.IU+I2R C.IU一I2R; D.U2/R
解析:该题不少学生选了D,其原因是同电源输出功率混淆,认为输出功率就是端电压与电流乘积,而这里不是电源输出而是电机输出.
答案:C
点评:(l)处理该类题目首先应当注意这是非纯电阻电路.
(2)这里的输入功率UI=转化成机械能的功率十转化成内能的功率.
[例6]某脉冲激光器的耗电功率为2×l03W,每秒钟输出10个光脉冲,每个脉冲持续的时间10-8s,携带的能量为 0.2J。则每个脉冲的功率为 W。该激光器将电能转化为激光能量的效率为
解析:P=W/t=2×107W。每秒 钟转化为光脉的能量是 E= 0.2J× 10=2 J,该激光器将电能转化为激光能量的效率η=E/E总=0.001
规律方法 1.电功、电功率的计算
(1)用电器正常工作的条件:
①用电器两端的实际电压等于其额定电压.
②用电器中的实际电流等于其额定电流.
③用电器的实际电功率等于其额定功率.
由于以上三个条件中的任何一个得到满足时,其余两个条件必定满足,因此它们是用电器正常工作的等效条件.灵活选用等效条件,往往能够简化解题过程.
(2)用电器接入电路时:
①纯电阻用电器接入电路中,若无特别说明,应认为其电阻不变.
②用电器实际功率超过其额定功率时,认为它将被烧毁.
[例7]微型吸尘器的直流电动机内阻一定,当加上0.3V的电压时,通过的电流为0.3A,此时电动机不转,当加在电动机两端的电压为2.0V时,电流为0.8A,这时电动机正常工作,则吸尘器的效率为多少?
 解析:当加0.3V电压时,电动机不转,说明电动机无机械能输出,它消耗的电能全部转化为热能,此时电动机也可视为纯电阻,则r=U1/I1=1Ω,当加2.0V电压,电流为0.8A时,电协机正常工作,有机械能输出,此时的电动机为非纯电阻用电器,消耗的电能等于转化机械能和热能之和。转化的热效率由P=I22r=0.82×1= 0.64 W计算,总功率由 P0=
I2U2=0.8×2.0=1.6W计算。所以电动机的效率为η=(P-P0)/P=60%。
解析:当加0.3V电压时,电动机不转,说明电动机无机械能输出,它消耗的电能全部转化为热能,此时电动机也可视为纯电阻,则r=U1/I1=1Ω,当加2.0V电压,电流为0.8A时,电协机正常工作,有机械能输出,此时的电动机为非纯电阻用电器,消耗的电能等于转化机械能和热能之和。转化的热效率由P=I22r=0.82×1= 0.64 W计算,总功率由 P0=
I2U2=0.8×2.0=1.6W计算。所以电动机的效率为η=(P-P0)/P=60%。
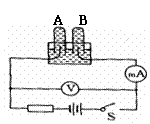
[例8]如图所示为电解水的实验装置,闭合开关S后观察到电压表的示数为6. 0 V,电流表的示数为100 mA.
(1)在实验过程中消耗了何种形式的能量?转化成了何种形式的能量?
(2)若通电10 min, A管中将生成多少毫升气体.
(3)已知每mol水被电解消耗280. 8 kJ的能量,则10 min内增加了多少化学能?
(4)在电解池中产生了多少内能,在该实验中两极间液体的电阻是多大?
解析:(1)在电解水的过程中,消耗了电能,转化了化学能和内能,由能量转化及守恒定律,消耗的电能等于化学能和内能的总和.
(2)因I=q/t,故q=It=0.1×600 C= 60 C.
到达阴极的板离于和电子结合成氢原子,再结合成氢分子.每个电子带电e=1. 6×10-19 C,在10min内,在阳极生成氢气的物质的量为:n=q/2eNA=60/(2×1. 6×10-19 × 6. 02×1023)mol=3.11×10-4mol
在标准状况下每摩尔氢气的体积为22.4L,所以在A管中生成氢气的体积:V=3.11×10-4×22.4 L=6.97 mL
(3) 10 min内增加的化学能,E化=3.11×10-4×280. 8 × 103J=87.3J
(4)由能量守恒定律求得电解池中产生的内能
Q=E电一E化=IUt一E化=6×0.I×600J-87.3J=272: 7 J.
再根据焦耳定律可求出电解池内两极间电阻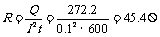
3.焦耳定律;电流通过一段只有电阻元件的电路时,在 t时间内的热量Q=I2Rt.
纯电阻电路中W=UIt=U2t/R=I2Rt,P=UI=U2/R=I2R
非纯电阻电路W=UIt,P=UI
2.电功率:电流做功的快慢,即电流通过一段电路电能转化成其它形式能对电流做功的总功率,P=UI
1.电功:电荷在电场中移动时,电场力做的功W=UIt,
电流做功的过程是电能转化为其它形式的能的过程.
3、 导体的伏安特性曲线:研究部分电路欧姆定律时,常画成I-U或U-I图象,对于线性元件伏安特性曲线是直线,对于非线性元件,伏安特性曲线是非线性的.
导体的伏安特性曲线:研究部分电路欧姆定律时,常画成I-U或U-I图象,对于线性元件伏安特性曲线是直线,对于非线性元件,伏安特性曲线是非线性的.
注意:①我们处理问题时,一般认为电阻为定值,不可由R=U/I认为电阻R随电压大而大,随电流大而小.
②I、U、R必须是对应关系.即I是过电阻的电流,U是电阻两端的电压.
[例1]来自质子源的质子(初速度为零),经一加速电压为800kV的直线加速器加速,形成电流强度为1mA的细柱形质子流。已知质子电荷e=1.60×10-19C。这束质子流每秒打到靶上的质子数为_________。假定分布在质子源到靶之间的加速电场是均匀的,在质子束中与质子源相距L和4L的两处,各取一段极短的相等长度的质子流,其中的质子数分别为n1和n2,则n1∶n2=_______。
 解:按定义,
解:按定义,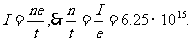
由于各处电流相同,设这段长度为l,其中的质子数为n个,
则由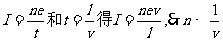 。而
。而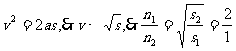
点评:解决该题的关键是:(1)正确把握电流强度的概念 I=Q/t而 Q=ne。所以n=Q/e=It/e,(2)质子源运动路程上的线密度与其瞬时速度成反比,因为I=neSv,所以当电流I一定时,n与v成反比.
[例2]用某种金属制成粗细均匀的导线,通以一定大小的恒定电流,过一段时间后,导线升高的温度( )
A.跟导线的长度成正比 B.跟导线的长度成反比
C.跟导线的横截面积成正比 D.跟导线的横截面积成反比
解析:金属导线的电阻为R=ρL/S,通电后产生的电热为Q=I2Rt=I2ρt/S.设金属导体升高的温度为ΔT,由热学知识可知导体需要的热量为 Q/=cmΔT= cρ密 LSΔT.电流产生的全部热量均被导线所吸收,即:I2ρt/S=cρ密 LSΔT,ΔT=I2ρt/cρ密LS2,上式说明了 D选项正确.
[例3]试研究长度为l、横截面积为S,单位体积自由电子数为n的均匀导体中电流的流动,在导体两端加上电压U,于是导体中有匀强电场产生,在导体内移动的自由电子(-e)受匀强电场作用而加速.而和做热运动的阳离子碰撞而减速,这样边反复进行边向前移动,可以认为阻碍电子运动的阻力大小与电子移动的平均速度v成正比,其大小可以表示成kv(k是常数).
(1)电场力和碰撞的阻力相平衡时,导体中电子的速率v成为一定值,这时v为
A.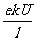 B.
B.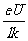 C.
C.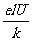 D.
D.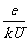
(2)设自由电子在导体中以一定速率v运动时,该导体中所流过的电流是___________.
(3)该导体电阻的大小为___________(用k、l、n、s、e表示).
[答案] 据题意可得kv=eE,其中E=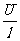 ,因此v=
,因此v=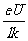 .据电流微观表达式I=neSv,可得I=
.据电流微观表达式I=neSv,可得I= ,再由欧姆定律可知R=
,再由欧姆定律可知R= .
.
2、适用于金属导电体、电解液导体,不适用于空气导体和某些半导体器件.
1、导体中的电流I跟导体两端的电压成正比,跟它的电阻R成反比。 I=U/R
15.[解析]⑴根据万有引力定律和向心力公式:
G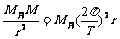 (1)
mg = G
(1)
mg = G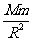 (2)
(2)
解(1)(2)得:r =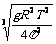 (3)
(3)
⑵设月球表面处的重力加速度为g月,根据题意:
V0=g月t/2 (4) g月 = GM月/r2
解(4)(5)得:M月 =2v0r2/Gt
[答案](1)r =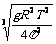 (2)M月 =2v0r2/Gt
(2)M月 =2v0r2/Gt
15.(启东市高三第一次调研卷.物理.14) 我国在2010年实现探月计划--“嫦娥工程”。同学们也对月球有了更多的关注。
⑴若已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的周期为T,月球绕地球的运动近似看做匀速圆周运动,试求出月球绕地球运动的轨道半径;
⑵若宇航员随登月飞船登陆月球后,在月球表面某处以速度v0竖直向上抛出一个小球,经过时间t,小球落回抛出点。已知月球半径为r,万有引力常量为G,试求出月球的质量M月
14.[解析]①卫星在离地600km处对卫星加速度为a,由牛顿第二定律
 又由
又由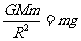 可得a=8 m/s2
可得a=8 m/s2
(2) 卫星离月面200km速度为v,由牛顿第二定律得:
卫星离月面200km速度为v,由牛顿第二定律得:
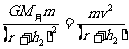 …由
…由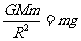 及M月/M=1/81
及M月/M=1/81
得:V2=2.53×106km2/s2
由动能定理,对卫星
W=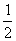 mv2-
mv2-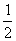 mv02
mv02
[答案](1)8 m/s2 (2)W=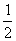 mv2-
mv2-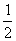 mv02
mv02
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com