
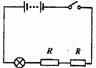
2、供电电路
供电电路一般由电源和滑动变阻器按一定的连接方式组成,滑动变阻器在供电电路中有两种接线方式:限流式和分压式如图.限流式可省一个耗电支路,分压式电压调节范围大,应根据需要选用.
 变阻器的分压与限流接法,虽然两种电路均可调节负载电阻电压和电流的大小,但在不同条件下,调节效果大不一样.
变阻器的分压与限流接法,虽然两种电路均可调节负载电阻电压和电流的大小,但在不同条件下,调节效果大不一样.
a.负载电阻的阻值Rx远大于变阻器的总电阻R,须用分压式电路.
b.要求负载上电压或电流变化范围较大,且从零开始连续可调,须用分压式电路
c.负载电阻的阻值Rx小于变阻器总电阻R或相差不多,且电压电流变化不要求从零调起时,可采取限流接法.
d两种电路均可使用的情况下,应优先采用限流式接法,因为限流接法总功率较小.
e.特殊问题中还要根据电压表和电流表量程以及电阻允许通过的最大电流值来反复推敲,以便能减小误差的连接方式为好.
1、测量电路
测量电路有两种方法:电流表内接法和电流表外接法.
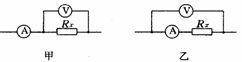 甲图中:
甲图中: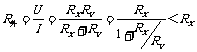 ,误差ΔR=R外-RX=
,误差ΔR=R外-RX=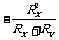
乙图中: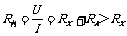 , 误差ΔR=R内-RX=RA
, 误差ΔR=R内-RX=RA
确定内接法还是外接法,有三种方法:
a直接比较法:当Rx >>RA时用内接法,当Rx<<Rv时用外接法.
b.临界值计算法:当内、外接法相对误差相等时,有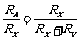
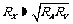 (RA<<Rv)为临界值.当
(RA<<Rv)为临界值.当 ,(即Rx为大电阻)时用内接法;当
,(即Rx为大电阻)时用内接法;当 (即Rx为小电阻)时用外接法;
(即Rx为小电阻)时用外接法;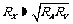 时内、外接法均可.
时内、外接法均可.
当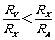 时,用电流表外接法;当
时,用电流表外接法;当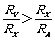 时,用电流表内接法.
时,用电流表内接法.
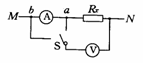 c.测试判断法:当Rx,RA,Rv大约值都不清楚时用此法.
c.测试判断法:当Rx,RA,Rv大约值都不清楚时用此法.
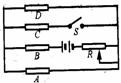
如图所示,将单刀双掷开关S分别接触a点和b点,若看到电流表读数变化较大,说明电压表分流影响较大,应该选用内接法;若看到电压表读数变化较大,说明电流表分压影响较大,应该选用外接法.
在测定金属电阻率电路中,由于电阻丝电阻较小,所以实验室采用电流表外接法;而测电池的电动势和内电阻,通常只采用电流表内接法.(对R来说)
4、含电容器电路的分析与计算
电容器是一个储存电能的元件.在直流电路中,当电容器充放电时,电路里有充放电电流,一旦电路达到稳定状态,电容器在电路中就相当于一个阻值无限大(只考虑电容器是理想的不漏电的情况)的元件,在电容器处电路看作是断路,简化电路时可去掉它.简化后若要求电容器所带电荷量时,可在相应的位置补上.分析和计算含有电容器的直流电路时,需注意以下几点:
(1)电路稳定后,由于电容器所在支路无电流通过.所以在此支路中的电阻上无电压降,因此电容器两极间的电压就等于该支路两端的电压.
(2)当电容器和用电器并联后接入电路时,电容器两极间的电压与其并联用电器两端的电压相等.
(3)电路的电流、电压变化时,将会引起电容器的充(放)电.如果电容器两端电压升高,电容器将充电;如果电压降低,电容器将通过与它并联的电路放电.电容器两根引线上的电流方向总是相同的,所以要根据正极板电荷变化情况来判断电流方向。
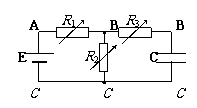 ⑷如果变化前后极板带电的电性相同,那么通过每根引线的电荷量等于始末状态电容器电荷量的差;如果变化前后极板带电的电性改变,那么通过每根引线的电荷量等于始末状态电容器电荷量之和。
⑷如果变化前后极板带电的电性相同,那么通过每根引线的电荷量等于始末状态电容器电荷量的差;如果变化前后极板带电的电性改变,那么通过每根引线的电荷量等于始末状态电容器电荷量之和。
[例15]如图电路中,电源内阻不计.为使电容器的带电量增大,可采取以下哪些方法()
A.增大R1; B.增大R2; C.增大R3 D.减小R1
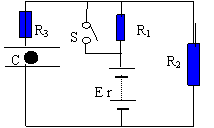 解析:由于在直流电路中稳定后电容器相当于断路,因此R3上无电流,电容器相当于和R2并联.为使电容器的带电量增大,根据Q=CU,应增大电容器C两端的电压。分析电路中的电压分配。只有增大R2或减小R1才能增大R2两端的电压(即电容器C两端的电压),从而增大电容器C的带电量。改变R3不能改变电容器的带电量。正确答案为BD.
解析:由于在直流电路中稳定后电容器相当于断路,因此R3上无电流,电容器相当于和R2并联.为使电容器的带电量增大,根据Q=CU,应增大电容器C两端的电压。分析电路中的电压分配。只有增大R2或减小R1才能增大R2两端的电压(即电容器C两端的电压),从而增大电容器C的带电量。改变R3不能改变电容器的带电量。正确答案为BD.
[例16]如图所示,E=10 V, r=1Ω, R1=R3=5 Ω, R2=4Ω,C=100μF。当S断开时,电容器中带电粒子恰好处于静止状态。求:
(1)S闭合后,带电粒子加速度的大小和方向;
(2)S闭合后流过R3的总电荷量。
解析:开始带电粒子恰好处于静止状态,必有qE=mg且qE竖直向上。S闭合后,qE=mg的平衡关系被打破。
S断开,带电粒子恰好处于静止状态,设电容器两极板间距离为d,有
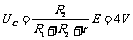 ,qUC/d=mg。S闭合后,
,qUC/d=mg。S闭合后,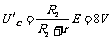
设带电粒子加速度为a,则qU/C/d-mg= ma,解得a=g,方向竖直向上。
(2 )S闭合后,流过R3的总电荷量等于电容器上电荷的增加量,所以ΔQ=C ( U/c一Uc)=4×10-4 C.
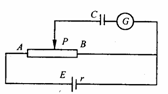 [例17]电动势为E、内电阻为r的电源与粗细均匀的电阻丝相联,组成如图所示的电路。电阻丝长度为L,电阻为R.C为平行板电容器,其相对面积为S,两板间的距离为d.在滑动触头向右滑的过程中,电流计中有电流通过,为什么?若电流计允许通过的最大电流为Im,求P滑动时,所允许的最大速度是多少?
[例17]电动势为E、内电阻为r的电源与粗细均匀的电阻丝相联,组成如图所示的电路。电阻丝长度为L,电阻为R.C为平行板电容器,其相对面积为S,两板间的距离为d.在滑动触头向右滑的过程中,电流计中有电流通过,为什么?若电流计允许通过的最大电流为Im,求P滑动时,所允许的最大速度是多少?
解析:电容器的电压等于电阻丝PB段上的电压,如果P不滑动,电阻丝PB段长度不变,加在电容C上的电压也不变,电流计G中无电流通过。若P向右滑动,PB段长度减少,电阻减少,电压也减小,电容器就要放电。电流计G中的电流就是电容器放电的电流。由于滑动的速度越大,电容器上电压减小越快,放电电流越大。因此电流计G允许通过电流的最大值就决定了P滑动的最大速度。
设滑动触头P滑动的速度为v,那么在Δt时间内滑过的距离为ΔL = vΔt .若P1,P2为滑动触头的初末位置.那么P1,P2与B点间的电压分别为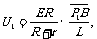
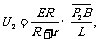
滑动触头P从P1滑至P2的过程中,触头P与B点间的电压减小量为
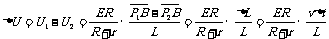
在此过程中,电容器的放电量为ΔQ=CΔU=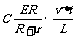 ,其中,电容器的电容为
,其中,电容器的电容为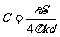
那么.根据电流的定义,流过电流计的电流为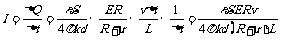
又因为流过电流计的电流I≤Im,所以触头P滑动时,所允许的最大速度为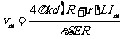
试题展示
 电路的测量
电路的测量
基础知识 一、电路设计
电路设计具有培养和检查创造性思维能力、分析综合能力以及实验能力等多方面的能力的特点,它包括测量电阻值Rx、电阻率ρ,电功率p和电源电动势E、内阻r.
电路设计的基本原则是:安全性好,误差小,仪器少,耗电少,操作方便.
伏安法实验电路一般可分为两部分:测量电路部分和供电电路部分.
3、电路中的能量关系的处理
要搞清以下概念:
 (1)电源的功率。电源消耗的功率、化学能转变为电能的功率、整个电路消耗的功率都是指εI或I2(R外+r)
(1)电源的功率。电源消耗的功率、化学能转变为电能的功率、整个电路消耗的功率都是指εI或I2(R外+r)
(2)电源的输出功率、外电路消耗的功率都是指:IU或Iε一 I2r或I2R外
(3)电源内阻消耗的功率:I2r
(4)整个电路中 P电源= P外十P内
[例11]电源输出功率和效率的讨论.
 分析:电源的输出功率为P出=I2R=
分析:电源的输出功率为P出=I2R=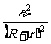 R=
R=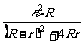 =
=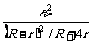
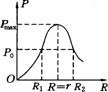
当R=r时,P出有最大值即Pm=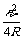 =
=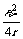 .P出与外电阻R的这种函数关系可用如图9-19的图象定性地表示.由图象还可知,对应于电源的非最大输出功率 P可以有两个不同的外电阻R1和R2,由图象还可知:当R<r时,若R增加,则P出增大;当R>r时,若R增大,则P 出减小.值得注意的是,上面的结论都是在电源的电动势ε和内电阻r不变的情况下适用.例如图9一20电路中ε=3v,r=0.5Ω,Ro= 1.5 Ω,变阻器的最大阻值R=10Ω.在R=?时,R消耗的功率才最大.此种情况可以把R0归入内电阻,即当R=r+Ro=2Ω时,R消耗功率最大为Pm=
.P出与外电阻R的这种函数关系可用如图9-19的图象定性地表示.由图象还可知,对应于电源的非最大输出功率 P可以有两个不同的外电阻R1和R2,由图象还可知:当R<r时,若R增加,则P出增大;当R>r时,若R增大,则P 出减小.值得注意的是,上面的结论都是在电源的电动势ε和内电阻r不变的情况下适用.例如图9一20电路中ε=3v,r=0.5Ω,Ro= 1.5 Ω,变阻器的最大阻值R=10Ω.在R=?时,R消耗的功率才最大.此种情况可以把R0归入内电阻,即当R=r+Ro=2Ω时,R消耗功率最大为Pm=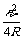 =
=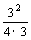 =9/8w;那么当R=?时,R0消耗的功率才最大呢?有些同学又会用了上述的方法来求解,把R归为内阻,调节R使内阻R+r=R0,这样会用是错误的!因为 Ro是定值电阻,由 P=I2R0知,只要电流最大,P就最大,所以当把R调到零时,R0上有最大功率.Pm/=
=9/8w;那么当R=?时,R0消耗的功率才最大呢?有些同学又会用了上述的方法来求解,把R归为内阻,调节R使内阻R+r=R0,这样会用是错误的!因为 Ro是定值电阻,由 P=I2R0知,只要电流最大,P就最大,所以当把R调到零时,R0上有最大功率.Pm/=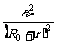 R0=
R0=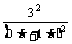 ×1.5=
×1.5=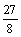 W.
W.
由上述分析可知,在研究电阻R上消耗的最大功率时,应注意区分“可变与定值”这两种情况,两种情况中求解的思路和方法是不相同的.
电源的效率η=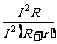 =
=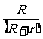 =
=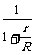 .所以当R增大时,效率η提高.当R=r,电源有最大输出功率时,效率仅为50%,效率并不高.
.所以当R增大时,效率η提高.当R=r,电源有最大输出功率时,效率仅为50%,效率并不高.
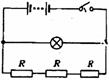
[例12]将一个标有“24 V、48 W’的电灯接在电动势ε=36 V.内阻r=2 Ω的直流电源下使用,今有“2Ω、50W”的定值电阻R若干只可供选用,请设计两种简单电路使电灯正常发光:
 (1)定值电阻与电灯串联作分压电阻使用;
(1)定值电阻与电灯串联作分压电阻使用;
(2)定值电阻与电灯并联作分流电阻使用(写出设计根据要点,画出电路图)
(3)在你设计的两种电路中,哪种方法较好?说明理由。
解析:电灯额定电流I0=P0/U0=2A.电阻R0=U02/P0=12Ω.定值电阻R的额定电流I=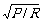 =5A。
=5A。
(1) R总=ε/I0 =36/2=18Ω,
 R串=R总一 R0 -r=18-12=4Ω=2R
R串=R总一 R0 -r=18-12=4Ω=2R
(2)R并=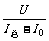 =
=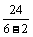 =6Ω=3R
=6Ω=3R
(3)第1种万法:电源消耗总功率 P1=I1ε=2×36=72W
效率ηl=P0/P1=48/72=67%。
第2种方法:电源消耗总功率P2=I总ε=6×36=216 W,效率η2=P0/P2=48/216=22%。
第1种万法好:节能.效率高
[例13]在图中,发电机的内阻r=0。1Ω,每根连接导线的电阻r1=0.1Ω,负载电阻R=22Ω,电路中的电流强度I=10A,求:(1)负载两端的电压UR;(2)外电路上的电压U端;(3)发电机的电动势;(4)整个外电路上消耗的功率P外;(5)负载上消耗的功率;(6)导线上消耗的功率;(7)发电机内部消耗的功率;(8)发电机的功率.
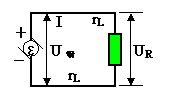 解析:(1)、负载两端的电压 UR=IR=10×22 V=220 V.
解析:(1)、负载两端的电压 UR=IR=10×22 V=220 V.
(2)外电路上的电压 U端=IR外=I(R十2rL)=10 ×(22+2 × 0.1)V=222 V.
(3)电源电动势 ε=U端十Ir=(222+10×0.1)V=223 V.
(4)外电路上消耗的功率 P外=IU端=10×222 W=2.2 kw.
(5)负载上消耗的功率 P负=IU负=10×220=2.2kw
(6)导线上消耗的功率 P导=2I2r=2×102 ×0.2W= 20 W
(7)发电机内部消耗的功率 P内=I2r=102×0.1w=10W
(8)发电机的功率P= Iε= 10 ×223 W= 2.23 kw
[例14]如图所示;电源的电动势为50V.电源内阻为1.0Ω,定值电阻R为14Ω.M为直流电动机,电枢电阻R为2.0Ω。电动机正常运转时,伏特表的读数为35V。求在100s的时间内电源做的功和电动机上转化为机械能的部分是多少。
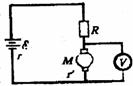 解析:由题设条件知r和R上的电压降之和为(ε-U),所以电路中的电流为 I=
解析:由题设条件知r和R上的电压降之和为(ε-U),所以电路中的电流为 I=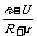 =
=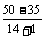 =1.0A
=1.0A
所以在100 s内电源做的功为
WE=εIt=50×1×100 J=5.0×103J。
在100s内电动机上把电能转化为机械能的部分是
ΔE=IUt-I2 r/t=(1.0×35×100一12×2×100)J=3.3×103J
(1)内、外电路
①内电路:电源两极(不含两极)以内,如电池内的溶液、发电机的线圈等.内电路的电阻叫做内电阻.
②外电路:电源两极,包括用电器和导线等.外电路的电阻叫做外电阻.
(2) 闭合电路的欧姆定律
①内容:闭合电路的电流跟电源的电动势成正比,与内、外电路的电阻之和成反比,即I=ε/(R+r)
②ε=U+Ir可见电源电势能等于内外压降之和;
③适用条件:纯电阻电路
(3)路端电压跟负载的关系
①路端电压:外电路的电势降落,也就是外电路两端的电压.U=ε-Ir, 路端电压随着电路中电流的增大而减小;
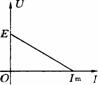 ②U一I关系图线
②U一I关系图线
当电路断路即I=0时,纵坐标的截距为电动势E;当外电路电压为U=0时,横坐标的截距I短 =E/r为短路电流;图线的斜率的绝对值为电源的内电阻.
(4).闭合电路的输出功率
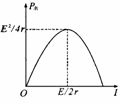 ①功率关系:P总=EI=U外I十U内I= UI+I2r,
①功率关系:P总=EI=U外I十U内I= UI+I2r,
②电源的输出功率与电路中电流的关系:P出=EI-I2r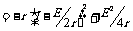
当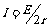 时,电源的输出功率最大,
时,电源的输出功率最大,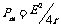
 ③电源的输出功率与外电路电阻的关系:
③电源的输出功率与外电路电阻的关系: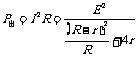
当R=r时也即I=E/2r时,电源的输出功率最大, 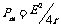
由图象可知,对应于电源的非最大输出功率P可以有两个不同的外电阻Rl和R2,不难证明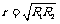 .由图象还可以看出:当R<r时,若R增大,则P出增大;当R>r时,若R增大,则P出减小.应注意:对于内外电路上的固定电阻,其消耗的功率仅取决于电路中的电流大小
.由图象还可以看出:当R<r时,若R增大,则P出增大;当R>r时,若R增大,则P出减小.应注意:对于内外电路上的固定电阻,其消耗的功率仅取决于电路中的电流大小
④电源的供电效率
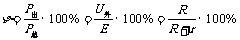
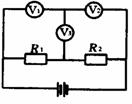
 [例1]如图所示,电压表 Vl、V2串联接入电路中时,示数分别为8 V和4 V,当电压表V2接入电路中时,如图(2)所示,示数为 10 V,求电源的电动势为多少?
[例1]如图所示,电压表 Vl、V2串联接入电路中时,示数分别为8 V和4 V,当电压表V2接入电路中时,如图(2)所示,示数为 10 V,求电源的电动势为多少?
解析:当两电压表接入电路时,电路中的电流强度为Il,当一个电压表接入电路时,电路中的电流强度为I2,则由图可知
I1=(ε一12)/r= 4/Rv2……①
I2=(ε-10)/r=10/Rv2……②
(l)÷(2)后得(ε一12)/(ε-10)=4/10解得 E= 13.3 V
点评:还可以根据串联电路的电压分配与电阻成正比列出关系式.(ε一12)/4=r/Rv2和(ε-10)/10=r/Rv2,等量代换后,即得E=13.3V.
 [例2]
如图所示,RB= 4Ω,A、C、D是额定电压和额定功率均相同的三个用电器、电源内阻是lΩ.S闭合后,当变阻器的电阻调为5Ω时,各用电器均正常工作.
[例2]
如图所示,RB= 4Ω,A、C、D是额定电压和额定功率均相同的三个用电器、电源内阻是lΩ.S闭合后,当变阻器的电阻调为5Ω时,各用电器均正常工作.
(1)S断开后,若仍要各用电器正常工作,变阻器电阻R应调为多少?
(2)S闭合和断开时, RB上的电功率之比PB∶PB/=?变阻器上消耗的功率之比 P∶ P/=?
解析:(1)在图所示的电路中,A、C、D三个用电器是并联的,且正常工作,其额定功率相等,说明三个用电器的电流均相等,设每个用电器的额定电流为I,
若S闭合,有3I=(ε-U)/(RB+R+r)………①
若 S断开,则有2I=(ε-U)/(RB+Rx+r)………②
由①、②解得Rx= 10Ω
(2)在 S闭合和断开两种情况下,电阻RB上消耗的电功率之比应为其通过电流的平方比 PB∶PB/=(3I/2I)2=9/4,变阻器上消耗的功率应等于通过的电流平方与电阻乘积之比P∶ P/=(3I/2I)2×(R/Rx)=9/8
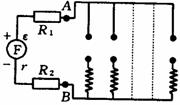 [例3]在图电路中,直流发电机ε=250V,r=3Ω:R1=R2=1Ω,电热器组中装有50只完全相同的电热器,每只电热器的额定电压为 200V,额定功率为1000W,其它电阻不计,并且不计电热器电阻随温度的变化.问:
[例3]在图电路中,直流发电机ε=250V,r=3Ω:R1=R2=1Ω,电热器组中装有50只完全相同的电热器,每只电热器的额定电压为 200V,额定功率为1000W,其它电阻不计,并且不计电热器电阻随温度的变化.问:
(1)当接通几只电热器时,实际使用的电热器都能正常工作?
(2)当接通几只电热器时,发电机输出功率最大?
(3)当接通几只电热器时,电热器组加热物体最快?
(4)当接通几只电热器时,电阻R1、R2上消耗的功率最大?
(5)当接通几只电热器时,实际使用的每只电热器中电流最大?
解析:不计用电器电阻随温度的变化,则每只电热器的电阻R0=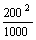 =40Ω,每只电热器的额定电流I0=
=40Ω,每只电热器的额定电流I0=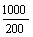 =5A
=5A
(1) 要使用电器正常工作,必须使电热器两端的实际电压等于额定电压200V ,因此干路电流

而每只电热器额定电流为5A,则电热器的只数n1=10/5=2只
(2)要使电源输出功率最大,必须使外电阻等于内*电阻,由此可得电热器总电阻为R=r-(R1+R2)=3-(1+1)=1Ω,故有n2=R0/R=40/1=40只
(3)要使电热器组加热物体最快,就必须使电热器组得到的电功率最大,把R1、R2视为等效(电源)内电阻,则其总电阻为
R/=R1+R2+r=1+l+3=5Ω 所以n3=R0/R/=40/5=8只,
(4)要使R1、R2上消耗功率最大,必须使其电流为最大,由此电路中总电阻必须是小.即当50只电热器全接通时,可满足要求.所以n4=50只.
(5)要使实际使用的每只电热器中电流最大.则须使UAB最大,这样A、B间的电阻应最大,所以n5=1只
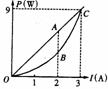 [例4]如图所示,直线AOC为某一电源的总功率P总随电流i变化的图线,抛物线OBC为同一直流电源内部热功率Pr随电流I变化的图象.若A、B对应的横坐标为2A,那么线段AB表示的功率及I=2A时对应的外电阻是( ).
[例4]如图所示,直线AOC为某一电源的总功率P总随电流i变化的图线,抛物线OBC为同一直流电源内部热功率Pr随电流I变化的图象.若A、B对应的横坐标为2A,那么线段AB表示的功率及I=2A时对应的外电阻是( ).
A.2W,0.5Ω; B.4W,2Ω;C.2W,lΩ;D.6W,2Ω;
解析:由图象知,直线OAC表示电源的P总-I的关系,即P总=ε·I
在C点,I=3A, P总=9W,所以 ε=P总/I=9/3V=3V
抛物线OBC表示电源的Pr-I的关系,即Pr=I2 r,
在C点,I=3A,Pr=9W,所以r=Pr/I2=9/32=lΩ
根据闭合电路的欧姆定律,当I=2A时,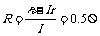
线段AB表示的功率即电源的输出功率,有PAB=UI=I2R=22×0.5=2W
规律方法 1、动态电路的分析与计算
动态电路变化的分析是根据欧姆定律及串、并联电路的性质,来分析电路中某一电阻变化而引起的整个电路中各部分电学量的变化情况,常见方法如下:
(1)程序法:基本思路是“部分→整体→部分” 部分电路欧姆定律各部分量的变化情况。
即R局增大减小→R总增大减小→I总增大减小→U总增大减小→I分U分
(2)直观法:即直接应用“部分电路中R、I、U的关系”中的两个结论。
①任一电阻R阻值增大,必引起该电阻中电流I的减小和该电阻两端电压U的增大
②任一电阻R阻值增大,必将引起与这并联的支路中电流I并的增大和与之串联的各电路电压 U串的减小。
(3)极限法:即因变阻器滑动引起电路变化的问题,可将变阻器的滑动端分别滑至两个极端去讨论。
(4)特殊值法。对于某些双臂环路问题,可以采取代入特殊值去判定,从而找出结论。
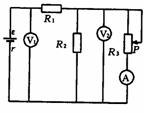 [例5]如图所示,当滑动变阻器的滑动片P向上端移动时,判断电路中的电压表、电流表的示数如何变化?
[例5]如图所示,当滑动变阻器的滑动片P向上端移动时,判断电路中的电压表、电流表的示数如何变化?
解析:先认清电表A测量R3中的电流,电表V2测量R2和R3并联的电压,电表V1测量路端电压.再利用闭合电路欧姆定律判断主干上的一些物理量变化:P向上滑,R3的有效电阻增大,外电阻R外增大,干路电流I减小,路端电压U增大,至此,已判断出V1示数增大.再进行分支上的分析:由I减小,知内电压U/和R1的端电压UR1减小,由U外增大知R2和R3并联的电压U2增大--判断出V2示数增大.由U2增大和R3有效电阻增大,无法确定A示数如何变化,这就要从另一条途径去分析:由V2示数增大知通过R2的电流I2增大,而干路电流I减小,所以R3中的电流减小,即A示数减小
说明:当电路中任一部分发生变化时,将引起电路中各处的电流和电压都随之发生变化,可谓“牵一发而动全身”.判断此类问题时,应先由局部的变化推出总电流的变化、路端电压的变化,再由此分析对其它各部分电路产生的影响.
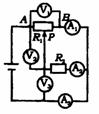 [例6]如图所示,R1和R2阻值相同,电源内阻不计,当滑动变阻器R1的滑动片P由A向B移动时,试分析电路中各电表示数的变化情况。
[例6]如图所示,R1和R2阻值相同,电源内阻不计,当滑动变阻器R1的滑动片P由A向B移动时,试分析电路中各电表示数的变化情况。
解析:先去掉伏特表,短接安培表,可见该电路为一分压电路,如图所示。
首先用程序法(极端法也行)判断:
当 P由 A→B时有RAP↑→R总↑→I总↓→U端↑
V1测出的是U端,示数增大,A3测的是总电流I总,示数变小。
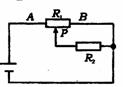 先假设RAP不变,用直观法可判知:比较可得,A2示数减小,V2增大,V3减小,而Al不能确定。
先假设RAP不变,用直观法可判知:比较可得,A2示数减小,V2增大,V3减小,而Al不能确定。
再利用特殊值法,令R1=R2=2R,则P位于AB两端点时,均有I1=ε/2R,当P位于R1中点时,有I1/=2ε/5R(按串、并联特征计算),显然I1/<I1,所以Al示数先减小后增大。
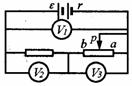 [例7]在如图所示的电路中,在滑线变阻器滑动片p由a滑到b的过程中,三只理想电压表示数变化的绝对值分别为ΔU1、ΔU2、ΔU3,则下列各组数据中可能出现的是( )
[例7]在如图所示的电路中,在滑线变阻器滑动片p由a滑到b的过程中,三只理想电压表示数变化的绝对值分别为ΔU1、ΔU2、ΔU3,则下列各组数据中可能出现的是( )
A.ΔU1=0、ΔU2=2 V、ΔU3=2 V B.ΔU1=1V、ΔU2=2 V、ΔU3=3 V
C:ΔU1=3V、ΔU2=1V、ΔU3=2V D.ΔU1=1V、ΔU2=1V、ΔU3=2V
解析:在闭合回路中,内、外电路电压降之和等于电源的电动势.在滑线变阻器的滑动片P由a滑到b的过程中,滑线变阻器连入电路中的电阻在减小,它的分压作用在减小,也就是电压表V3的示数要减小.由于滑线变阻器连入电路中的电阻在减小,由闭合回路的欧姆定律可知电路的总电流是增大的,电压表V2的示数是增大的.电压表V1测量的是电源的路端电压U,由U=ε-Ir式可知,电压表V1的示数变化反映了内电路上电压的变化值,且它们大小相等,符号相反(路端电压是减小的,但是内电路上的电压降U/是增大的).由ε=U+U/可知,由于电源的电动势ε不变,在闭合回路中,电压的变化量之和就为零,也可以说是电压减小的值与电压增大值之和相等,即ΔU1十ΔU2=ΔU3,根据此式可以排除 C选项,对于A选项,由于ΔU1是反映电源内电路上的电压降的变化,电源有内阻,ΔU1=0显然是错误的,所以只有B和D选项是正确的.
点评:路端电压 U等于外电路上各部分电压降之和,并不意味着应有ΔU1=ΔU2十ΔU3。(因为题设中 强调这是三只理想电压表示数变化的绝对值).由于是滑线变阻器的电阻变小,它两端的电压减小,从而导致其余电阻(包括内电阻)的分压作用增大,应有的关系式是第三只电压表中示数的减小量应等于其它两电压表示数变化量的绝对值之和.
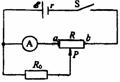 [例8]如图所示,安培表为理想电表,电源电动势为6V、内阻为1Ω,滑动变阻器的总电阻为11Ω,电阻R0为3Ω,问当S闭合时,变阻器的滑动触头P在R上滑动时,电流表的读数范围为多少?
[例8]如图所示,安培表为理想电表,电源电动势为6V、内阻为1Ω,滑动变阻器的总电阻为11Ω,电阻R0为3Ω,问当S闭合时,变阻器的滑动触头P在R上滑动时,电流表的读数范围为多少?
解析:当 S闭合后,电路中的总电流为
I=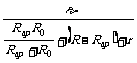 =
=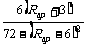
U1=U0,I1Rap=(I-I1)R0,I1=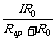 =
=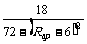
当Rap=6Ω时,Il有最小值。电流表的读数为Il=18/72=0.25A
当Rap=0时,即滑动触头P位于a端时,I1有最大值。电流表的读数为I1/=18/(72-36)=0.5A.
所以电流表的读数范围为 0.25A≤I≤ 0.5A;
2、电路故障分析与黑盒子问题
闭合电路黑盒。其解答步骤是:
①将电势差为零的两接线柱短接
②在电势差最大的两接线柱间画电源
③根据题给测试结果,分析计算各接线柱之间的电阻分配,并将电阻接在各接线柱之间。
[例9]如图所示的电路中,灯泡A和B原来都是正常发光。忽然灯泡B比原来变暗了些,而灯泡A比原来变亮了些,试判断电路中什么地方出现断路的故障?(设只有一处出现了故障)
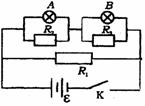 解析:依题意,整个电路只有一处发生了断路,下面分别对不同区域进行讨论:
解析:依题意,整个电路只有一处发生了断路,下面分别对不同区域进行讨论:
(1)若R1断路.电路中总电阻变大.电流变小.路端电压升高.A、B两灯均未亮.不合题意。
(2)若R3断路。B与R3并联.该段电路中电阻变大,电压升高,B中的电流增大,B灯变亮,不合题意
(3)若R2断路,A与R2并联,这段电路中电阻变大,使总电阻变大,总电流变小,各部分压降变小,A灯两端电压升高,A中电流增大,A灯变亮;因B灯两端电压减小,B灯中电流变小,B灯变暗,与题中条件相符。
 (4)4灯、B灯所在支路或其他部分发生断路,则两灯均不会发光,不合题意,故应是R2断路。
(4)4灯、B灯所在支路或其他部分发生断路,则两灯均不会发光,不合题意,故应是R2断路。
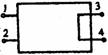
[例10]一盒子里装有由导线和几个阻值相同的电阻组成的电路,盒外有接线柱1、2、3、4,已知1、2间的电阻是1、3间电阻的1.5倍,是2、4间电阻的3倍,而3、4间没有明显电阻,欲使盒内电路所含电阻数最少,请画出盒内的电路图。
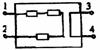 解析:①因3、4间没有明显电阻,将3、4短路得图.
解析:①因3、4间没有明显电阻,将3、4短路得图.
②依题意,Rl2=1.5Rl3=3R24,为使电阻数最少,取 R24为一个电阻, R12为三个电阻串联, R13为二个电阻串联。根据R12为三个电阻串联可把图补画成图。
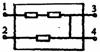 ③再满足R24为一个电阻和R23为二个电阻串联,把图又进而画成图,于是得所求结果。
③再满足R24为一个电阻和R23为二个电阻串联,把图又进而画成图,于是得所求结果。
3.电动势是标量.要注意电动势不是电压;
2.电动势:非静电力搬运电荷所做的功跟搬运电荷电量的比值,ε=W/q。表示电源把其它形式的能转化成电能本领的大小,在数值上等于电源没有接入电路时两极板间的电压,单位:V
1.电源是将其它形式的能转化成电能的装置.
①并联电路中各支路两端的电压相同.U=U1=U2=U3……
②并联电路子路中的电流等于各支路的电流之和I=I1+I2+I3=……
③并联电路总电阻的倒数等于各个导体的电阻的倒数之和。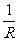 =
=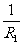 +
+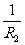 +…+
+…+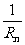 ,当并联电路是由n个相同的电阻R并联而成时,总电阻R总=
;当并联电路只有两个支路时,则总电阻为R总=
,当并联电路是由n个相同的电阻R并联而成时,总电阻R总=
;当并联电路只有两个支路时,则总电阻为R总=
④并联电路中通过各个电阻的电流踉它的阻值成反比,即I1R1=I2R2=…=InRn= U.
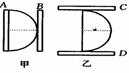 ⑤并联电路中各个电阻消耗的功率跟它的阻值成反比,即P1R1=P2R2=…=PnRn=U2.
⑤并联电路中各个电阻消耗的功率跟它的阻值成反比,即P1R1=P2R2=…=PnRn=U2.
[例1]如图所示,P为一块均匀的半圆形薄电阻合金片,先将它按图甲方式接在电极A、B之间,测出电阻为R,然后再将它按图乙方式接在C、D之间,这时P的电阻为( )
A·R; B·½R ;C·;R/4; D·4R
简析:将半圆形合金片从中间(图中虚线所示)割开,分成完全相同的两块,设每块电阻力R0,则图中甲连接方式相当于两个电阻并联,图乙连接相当于两个电阻串联.
 RAB=R0/2=R RCD=2R0=4R答案:D
RAB=R0/2=R RCD=2R0=4R答案:D
点评:巧妙选取相同的电阻,运用电阻的串并联特点来分析是解决此题的特点.
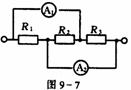
[例2]如图9-7中三个R1、R2、R3,电流表的内阻忽略不计,则通过三个电阻的电流强度之比和两个电流表读数之比各为多少?
解析:原图可变换成附图所示电路,三个电阻组成并联电路.流过三个电阻电流强度之比I1:I2:I3=1/ R1:1/ R2:1/ R3=R2R3:R1R3:R1R2
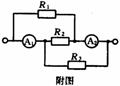 电流表A1和A2的读数之比I1/:I2/=(I2+ I3):(I1+ I2)=R1(R2+R3):R3(R1+R2)
电流表A1和A2的读数之比I1/:I2/=(I2+ I3):(I1+ I2)=R1(R2+R3):R3(R1+R2)
答案:I1:I2:I3=1/ R1:1/ R2:1/ R3,I1/:I2/=R1(R2+R3):R3(R1+R2)
[例3]图中电源电压U=5 V,内阻不计,V1、V2、V3、三个电压表的内电阻相同,其中V1、V2的读数分别为3V、2V,试求电压表V3的读数.
 简析:V1表的读数大于V2表的读数,V1表通过的电流I1大于V2表通过的电流I2, 并且等于V2表和V3表通过的电流之和,
简析:V1表的读数大于V2表的读数,V1表通过的电流I1大于V2表通过的电流I2, 并且等于V2表和V3表通过的电流之和,
即I1=I2十I3, 三个电压表的内阻相同,设为RV,则
I1RV= I2 RV十I3 RV
得:V1=V2+V3
V3=V1-V2=3V-2V=1V
点评:电压表的示数为本身的电压值,此题是把三个电压表当成三个相同的电阻来讨论的.
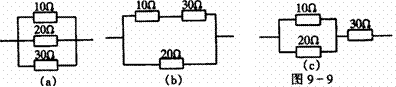
[例4]有三个电阻,其阻值分别为10 Ω、20Ω、30Ω,现在它们分别按不同方式连接后加上相同的直流电压,问:
(1)在总电路上可能获得的最大电流和最小电流之比为多少?
(2)对20Ω电阻来说,在各种可能连接方式中能使它获得最大功率的,有哪些连接方式?获得最小功率的有哪些连接方式?(只要求画电路图表示)
解析:如图所示(1)在电压不变的情况下,三电阻并联时总电阻最小,电流最大;三电阻串联时总电阻最大,电流最小.
 =
=  +
+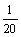 +
+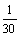 ,R并=60/11Ω R串=10+20+30,R串=60 Ω,I最大/I最小=R串/R并=11
,R并=60/11Ω R串=10+20+30,R串=60 Ω,I最大/I最小=R串/R并=11
(2)使20 Ω电阻获得最大功率的连接方式有:a、b,获得最小功率的连接方式是C。
答案:(1)11;(2)20 Ω电阻获得最大功率的是 a、b,最小功率的是C.
[例5]如图所示,A、B两点间的电压为U,C1= nC2,两个完全相同的电压表的示数分别为:
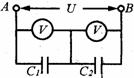 A.U1=U/(n+1),U2=nU/(n+1); B.U1=U/2,U2=U/2;
A.U1=U/(n+1),U2=nU/(n+1); B.U1=U/2,U2=U/2;
C.U1=nU/(n+1),U2=U/(n+1) D.无法判断两电压表的示数
解析:电压表串联接在电压U上,所示两只相同的电压表的分压作用相同,它们的示数相同,均为U/2.而两电容器是分别与两电压表并联,两电容器两端的电压分别与两电压表两端的电压相等,所以是B选项正确.
[点评]两电容器是串联接在电路上,若是认为两电压表是测电容器两端的电压,这就犯了定势思维的错误、电容器两端的电压不能用电压表来测量,只能用静电计测量,不要把电压表看成是测电压的,而应把两电压表看成两个相同的电阻串联接在电源上,而电容器两端的电压在电路中总是等于与它并联的电阻两端的电压.在阻容电路中,电容器两端的电压总是等于与它并联的电阻两端的电压,这是一个基本原则.
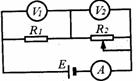 [例6]图中的 A为理想电流表,V1和V2为理想电压表,R1为定值电阻,R2为可变电阻,电池E内阻不计,下列说法中不正确的是
[例6]图中的 A为理想电流表,V1和V2为理想电压表,R1为定值电阻,R2为可变电阻,电池E内阻不计,下列说法中不正确的是
A.R2不变时,V2读数与A读数之比等于R1
B.R2不变时,V1读数与A读数之比等于R1
C.R2改变一定量时,V2读数的变化量与V1读数变化量之和一定为零
D.R2改变一定量时,V2读数的变化量与V1读数变化量之和不一定为零
解析:根据电路的连接形式可知:任意一个电压表的读数与电流表的读数之比均等于与电压表并联的电阻,所以B选项正确;电池的内阻不计,说明电源两端电压不变,则两电压表之和不变,而当R2变化时,则两电压表的变化和一定为零(一个增加,一个减小),C选项正确.
点评:本题为高考试题,考查的是对电路连接形式的认识,两电压表分两电阻并联,当一个电阻变化时,它的分压作用变化,导致另一个电阻的分用也发生了变化.
规律方法 1、电路结构分析
电路的基本结构是串联和并联,分析混联电路常用的方法是:
节点法:把电势相等的点,看做同一点.
回路法:按电流的路径找出几条回路,再根据串联关系画出等效电路图,从而明确其电路结构
其普遍规律是:⑴凡用导线直接连接的各点的电势必相等(包括用不计电阻的电流表连接的点)。
⑵在外电路,沿着电流方向电势降低。
⑶凡接在同样两个等势点上的电器为并联关系。
⑷不加声明的情况下,不考虑电表对电路的影响。
[例7]图中所示电路由8个不同的电阻组成,已知R1=12 Ω,其余电阻阻值未知,测得A、B之间总电阻为4Ω。今将R1换成6Ω的电阻,则A、B间的总电阻变为 Ω。
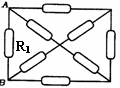 解析:利用等效代换的办法处理:即将除去R1之后的7个不同的电阻对A、B两点间的等效阻值设为R,则总的对A、B间的等效电阻值就为R1与R之并联等效值,由并联电路规律有
解析:利用等效代换的办法处理:即将除去R1之后的7个不同的电阻对A、B两点间的等效阻值设为R,则总的对A、B间的等效电阻值就为R1与R之并联等效值,由并联电路规律有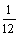 +
+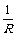 =
=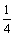 ,
, +
+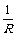 =
=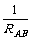 ,联立求得RAB=3Ω。
,联立求得RAB=3Ω。
[例8] 已知如图,两只灯泡L1、L2分别标有“110V,60W”和“110V,100W”,另外有一只滑动变阻器R,将它们连接后接入220V的电路中,要求两灯泡都正常发光,并使整个电路消耗的总功率最小,应使用下面哪个电路?
 A.
B.
C.
D.
A.
B.
C.
D.
解:A、C两图中灯泡不能正常发光。B、D中两灯泡都能正常发光,它们的特点是左右两部分的电流、电压都相同,因此消耗的电功率一定相等。可以直接看出:B图总功率为200W,D图总功率为320W,所以选B。
[例9]电饭锅是一种可以自动煮饭并自动保温,又不会把饭烧焦的家用电器。如图,它的电路由控制部分AB和工作部分BC组成。K1是限温开关,手动闭合,当温度达到103℃时自动断开,不能自动闭合.K2是自动开关,当温度超过800C时自动断开,温度低于700C时自动闭合。R2是限流电阻,阻值2140 Ω, R 1是工作电阻,阻值60Ω.锅中放好适量的米和水,插上电源(220'V,50 Hz),手动闭合K1后,电饭锅就能自动煮好米饭并保温。(1)简述手动闭合K1后,电饭锅加热、保温过程的工作原理。(2)加热过程电饭锅消耗的电功率P1是多大?K1,K2都断开时电饭锅消耗的电功率P2是多大?(3)若插上电源后没有手动闭合K1,能煮熟饭吗?为什么?
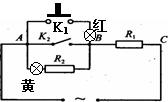 解析:(1)插上电源,手动闭合K1后由于室温肯定低于700C所以当时K2也是闭合的,红灯亮,所以R2被短路,只有R1工作,功率P1较大,使米和水被加热,当温度升到800C时K2断开。但K1仍闭合,R2仍被短路,功率仍为P1,所以温度继续升高,把水烧开,这时温度将保持在1000C直到水分蒸发完毕,温度继续升高到1030C时K1断开且不再自动闭合,这时饭已煮好,R1,R2串联,黄灯亮,热功率P2较小,电饭锅发出的电热小于它向外释放的热,温度开始降低,当温度降低到700C时,K2自动闭合,功率又变为P1,使饭的温度升高,到800C时K2自动断开,温度又开始降低……如此使电饭锅处于保温状态,直到关闭电源。
解析:(1)插上电源,手动闭合K1后由于室温肯定低于700C所以当时K2也是闭合的,红灯亮,所以R2被短路,只有R1工作,功率P1较大,使米和水被加热,当温度升到800C时K2断开。但K1仍闭合,R2仍被短路,功率仍为P1,所以温度继续升高,把水烧开,这时温度将保持在1000C直到水分蒸发完毕,温度继续升高到1030C时K1断开且不再自动闭合,这时饭已煮好,R1,R2串联,黄灯亮,热功率P2较小,电饭锅发出的电热小于它向外释放的热,温度开始降低,当温度降低到700C时,K2自动闭合,功率又变为P1,使饭的温度升高,到800C时K2自动断开,温度又开始降低……如此使电饭锅处于保温状态,直到关闭电源。
(2)加热过程电饭锅消耗的电功率P1=U2/R1=807W;K1, K2都断开时,电饭锅消耗的电功率P2=U2/(R1+R2)=22 W.
(3)若K1未闭合,开始K2总是闭合的,R2被短路,功率为P1,当温度上升到800C时,K2自动断开,功率降为P2,温度降低到700C,K2自动闭合……温度只能在700C-800C变化,不能把水烧开,不能煮熟饭.
[例10]在图所示的电路中,A、B、C分别表示理想电流表或电压表,它们的示数以安或伏为单位.当电键S闭合后,A、B、C三表示数分别为1、2、3时,灯L1、L2正好均正常发光.已知灯L1、L2的额定功率之比为3∶1,则可判断
A.A、B、C均为电流表 B.A、B、C均为电压表
C.B为电流表,A、C为电压表 D.B为电压表,A、C为电流表
 解答:若三个表均为电流表,则电路出现短路,灯不可能正常发光,故选项A错;若三个表均为电压表,则电路出现断路,灯亦不能正常发光,故选项B错;若B为电流表,A和C为电压表,则两灯串联,A表测L1的电压,C表测L2的电压,即为
解答:若三个表均为电流表,则电路出现短路,灯不可能正常发光,故选项A错;若三个表均为电压表,则电路出现断路,灯亦不能正常发光,故选项B错;若B为电流表,A和C为电压表,则两灯串联,A表测L1的电压,C表测L2的电压,即为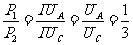 ≠
≠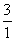 ,故选项C错;
,故选项C错;
若B为电压表,A和C为电流表,则两灯并联,A表测L2的电流,C表测L1的电流,故有
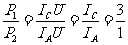 ,故选项D正确.[答案] D
,故选项D正确.[答案] D
2、电表的改装
(1)灵敏电流表(也叫灵敏电流计):符号为?,用来测量微弱电流,电压的有无和方向.其主要参数有三个:①内阻Rg.②满偏电流Ig:即灵敏电流表指针偏转到最大刻度时的电流,也叫灵敏电流表的电流量程.③满偏电压Ug:灵敏电流表通过满偏电流时加在表两端的电压.以上三个参数的关系Ug= Ig Rg.其中Ig和Ug均很小,所以只能用来测量微弱的电流或电压.
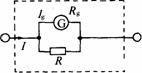 (2)电流表:符号?,用来测量电路中的电流,电流表是用灵敏电流表并联一个分流电阻改装而成.如图所示为电流表的内部电路图,设电流表量程为I,扩大量程的倍数n=I/Ig,由并联电路的特点得:Ig·Rg=(I-Ig)R,
(2)电流表:符号?,用来测量电路中的电流,电流表是用灵敏电流表并联一个分流电阻改装而成.如图所示为电流表的内部电路图,设电流表量程为I,扩大量程的倍数n=I/Ig,由并联电路的特点得:Ig·Rg=(I-Ig)R,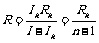
内阻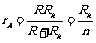 ,由这两式子可知,电流表量程越大,Rg越小,其内阻也越小.
,由这两式子可知,电流表量程越大,Rg越小,其内阻也越小.
 (3)电压表:符号?,用来测量电路中两点之间的电压.电压表是用灵敏电流表串联一个分压电阻改装而成,如图所示是电压表内部电路图.设电压表的量程为U,扩大量程的倍数为n=U/Ug,由串联电路的特点,得:
(3)电压表:符号?,用来测量电路中两点之间的电压.电压表是用灵敏电流表串联一个分压电阻改装而成,如图所示是电压表内部电路图.设电压表的量程为U,扩大量程的倍数为n=U/Ug,由串联电路的特点,得:
U=Ug+IgR, Ig =Ug /Rg, 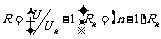
 电压表内阻
电压表内阻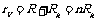 ,由这两个式子可知,电压表量程越大,分压电阻就越大,其内阻也越大.
,由这两个式子可知,电压表量程越大,分压电阻就越大,其内阻也越大.
(4)半值分流法(也叫半偏法)测电流表的内阻,其原理是:
当S1闭合、S2打开时: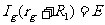
当S2再闭合时: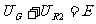 ,
,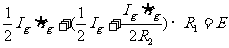
联立以上两式,消去E可得: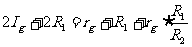
得: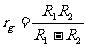 可见:当R1>>R2时, 有:
可见:当R1>>R2时, 有: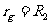
(5)非理想电表对电路的影响不能忽略,解题时应把它们看作是能显示出本身电压或电流的电阻器.
①用电压表测得的电压实际上是被测电路与电压表并联后两端的电压,由于电压表内阻不可能无限大,因此测得的电压总比被测电路两端的实际电压小,表的内阻越大,表的示数越接近于实际电压值.
②用电流表测得的电流,实质上是被测量的支路(或干路)串联一个电阻(即电流表内阻)后的电流.因此,电流表内阻越小,表的示数越接近于真实值.
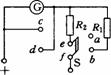 [例11]电流一电压两用电表的电路如图所示.已知图中S是双刀双掷开关,a, b,c、d,e、f为接线柱.双刀双掷开关的触刀掷向a,b,e与a接通,f与b接通;掷向c, d, e与c接通,f与d接通.电流表G的量程是0. 001
A,内阻是100Ω,电阻R1的阻值为9900Ω, R2的阻值是1.0l Ω,
[例11]电流一电压两用电表的电路如图所示.已知图中S是双刀双掷开关,a, b,c、d,e、f为接线柱.双刀双掷开关的触刀掷向a,b,e与a接通,f与b接通;掷向c, d, e与c接通,f与d接通.电流表G的量程是0. 001
A,内阻是100Ω,电阻R1的阻值为9900Ω, R2的阻值是1.0l Ω,
(1)触刀掷向a,b时,此两用表是什么表?量程是多大?
(2)触刀掷向c, d时,此两用表是什么表?量程是多大?
分析:用?改装成电流表时需要并联一个电阻, ?改装成电压表时需要串联一个电阻,根据这个原理可以判断出是什么表,并算出其量程.
解析:(1)触刀掷向ab时,R1与?串联,是电压表,其量程为U=Ig(R1+Rg)=0.001×(100+9900)=10V.
(2)触刀掷向cd时,R2与?并联,是电流表,其量程为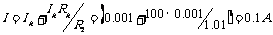
[例12]如图所示,四个相同的表头分别改装成两个安培表和两个伏特表。安培表A1的量程大于A2的量程,伏特表V1的量程大于V2的量程,把它们按图接入电路,则
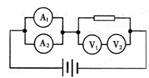 安培表A1的读数
安培表A2的读数;
安培表A1的读数
安培表A2的读数;
安培表A1的偏转角 安培表A2的偏转角;
伏特表V1的读数 伏特表V2的读数;
伏特表V1的偏转角 伏特表V2的偏转角;
(填“大于”,“小于”或“等于”)
解:两电流表并联,两表头两端的电压相同,流过的电流相同,故偏角相同,但因A1的量程大,故A1的示数大于A2的示数. 当把V1和V2串联使用时,组成电压表的电流表和分压电阻都是串联关系,通过完全相同的两只电流表的电流强度也相等,指针偏转角度相等.根据串联电路的电压分配关系,分配在V1和V2两端电压,即V1和V2读数之比等于两只电压表的内阻之比. 伏特表V1的量程大,所以读数大。
[例13]将两个相同的表头,分别改装成一只电流表和一只电压表,一个同学在做实验时误将这两个表串联起来,则
A.两表指针都不偏转 B.两表指针偏角相同
C.电流表指针有偏转,电压表指针几乎不偏转
D.电压表指针有偏转,电流表指针几乎不偏转
解答:把完全相同的表头,分别改制成一只电流表和一只电压表,串联接入电路中时,电流表中均有电流通过,两表指针都偏转,只是电压表中的电流表处在干路中通过的电流大,偏转角也大.
[例14]电源的电动势和内阻都保持一定,现用两个不同的电压表先后直接接到电源的两极上,电压表Ⅰ的读数是U1,电压表Ⅱ的读数是U2,已知电压表的内阻依次是R1、R2,且R1>R2,那么由于两电压表内阻不同,将是
A.U1一定小于U2 B.U1一定大于U2
C.若将两个电压表同时并接在电源的两极时,读数一定不同
D.若将两个电压表串联后接在电源的两极时,两电压表读数之和一定大于U1
解答:因R1>R2,则用电压表I测量时电路总电阻大于用电压表Ⅱ测量.由闭合电路欧姆定律可知I1<I2,因此,用电压表Ⅰ测量时因内电压小而路端电压大,即U1>U2.若两个电压表并联测量时,因两电压表并联,则测量电压必相同.若两电压表串联接在电源两极,因总电阻大于R1,总电源小于I1,故内电压必小于单独用电压表Ⅰ测量时的内电压,因此,路端电压(即两电压表读数之和)一定大于U1.答案BD
试题展示
 闭合电路的欧姆定律
闭合电路的欧姆定律
基础知识 一、电源
2.部分电路欧姆定律的应用
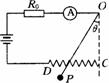 [例9]如图所示是一种测定风作用力的仪器原理图,P为金属球,悬挂在一细长金属丝下面,O是悬点,R0是保护电阻,CD是水平放置的光滑电阻丝,与细金属丝始终保护良好接触.无风时,金属丝与电阻丝在C点接触,此时?示数为I0;有风时金属丝将偏转一角度θ,角θ与风力大小有关,设风力方向水平向左,OC=h,CD=L,金属球质量为m,电阻丝单位长度的阻值为k,电源内阻和金属丝电阻不计,金属丝偏角为θ时,?的示数为I/,此时风力为F,试写出:
[例9]如图所示是一种测定风作用力的仪器原理图,P为金属球,悬挂在一细长金属丝下面,O是悬点,R0是保护电阻,CD是水平放置的光滑电阻丝,与细金属丝始终保护良好接触.无风时,金属丝与电阻丝在C点接触,此时?示数为I0;有风时金属丝将偏转一角度θ,角θ与风力大小有关,设风力方向水平向左,OC=h,CD=L,金属球质量为m,电阻丝单位长度的阻值为k,电源内阻和金属丝电阻不计,金属丝偏角为θ时,?的示数为I/,此时风力为F,试写出:
(1)F与θ的关系式.
 (2)F与I/的关系式.
(2)F与I/的关系式.
解析:(1)有风力时;对金属球P,受力如图,F=F1sinθ;mg=F1cosθ;F=mgtanθ
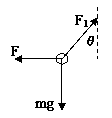 (2)无风时,电路中U=I0(R0+kL)
(2)无风时,电路中U=I0(R0+kL)
有风力时,电路中U=I/(R0+kL/), L/=L-htanθ
由以上各式解得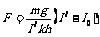
思考:本题你是怎样将实际问题抽象成简单的物理模型的?
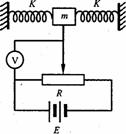 [例10]图为一种加速仪的示意图,质量为m的振子两端连有劲度系数均为K的轻弹簧,电源动势为E,不计内阻,滑动变阻器的总阻值为R,有效长度为L,系统静止时滑动触头位于滑动变阻器正中,这时电压表指针恰好在刻度盘正中。求:
[例10]图为一种加速仪的示意图,质量为m的振子两端连有劲度系数均为K的轻弹簧,电源动势为E,不计内阻,滑动变阻器的总阻值为R,有效长度为L,系统静止时滑动触头位于滑动变阻器正中,这时电压表指针恰好在刻度盘正中。求:
(1)系统的加速度a(以向右为正)和电压表读数U的函数关系式。
(2)将电压表刻度改为加速度刻度后,其刻度是均匀的还是不均匀的?为什么?
(3)若电压表指针指在满刻度的3/4位置,此时系统的加速度大小和方向如何?
解析:设加速度a向右,m向左平移了x,对m用牛顿第二定律有2Kx=ma;根据部分电路欧姆定律和电阻定律,电压表示数与左段电阻成正比,因此也和x成正比,所以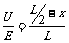 ,两式解得
,两式解得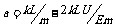 .
.
可见,a与U为一次函数关系,所以将电压表刻度改为加速度刻度后,其刻度是均匀的。
因为系统静止时滑动触头位于滑动变阻器正中,电压表指针恰好在刻度盘正中,U=E/2,所以电压表指针指在满刻度的3/4位置时,U=3E/4,带入a与U的一次函数关系式,得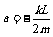 ,负号表示加速度方向向左。
,负号表示加速度方向向左。
试题展示
 散
串并联及混联电路
散
串并联及混联电路
基础知识 一、串联电路
①电路中各处电流相同.I=I1=I2=I3=……
②串联电路两端的电压等于各电阻两端电压之和.U=U1+U2+U3……
③串联电路的总电阻等于各个导体的电阻之和,即R=R1+R2+…+Rn
④串联电路中各个电阻两端的电压跟它的阻值成正比,即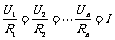
⑤串联电路中各个电阻消耗的功率跟它的阻值成正比,即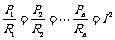
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com