
4.某服装制造商现有10m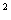 的棉布料,10m
的棉布料,10m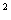 的羊毛料,和6 m
的羊毛料,和6 m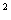 的丝绸料。做一条裤子需要1 m
的丝绸料。做一条裤子需要1 m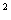 的棉布料,2 m
的棉布料,2 m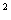 的羊毛料,1m
的羊毛料,1m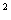 的丝绸料。一条裙子需要1 m
的丝绸料。一条裙子需要1 m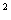 的棉布料,1 m
的棉布料,1 m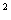 的羊毛料,1m
的羊毛料,1m 的丝绸料。一条裤子的收益是20元,一条裙子的收益是40元。为了使收益达到最大,需要同时生产这两种服装,请你列出生产这两种服装件数所满足的数学关系式,并画出图形。
的丝绸料。一条裤子的收益是20元,一条裙子的收益是40元。为了使收益达到最大,需要同时生产这两种服装,请你列出生产这两种服装件数所满足的数学关系式,并画出图形。
3.已知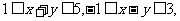 求
求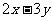 的取值范围。
的取值范围。
2.给定下面的线性规划问题:求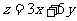 的最大值与最小值,使
的最大值与最小值,使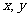 满足约束条件
满足约束条件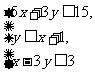 要使目标函数只有最小值而无最大值,请你改造条件中的一个不等式,那么新的约束条件应该是______________________。
要使目标函数只有最小值而无最大值,请你改造条件中的一个不等式,那么新的约束条件应该是______________________。
1.不等式组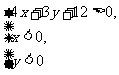 表示的平面区域内的整点坐标是_________________________
表示的平面区域内的整点坐标是_________________________
2. 电视台应某企业之约播放两套连续剧。其中,连续剧甲每次播放时间为80min,其中广告时间为1min,收视观众为60万;连续剧乙每次播放时间为40min,其中广告时间为1min,收视观众为20万。已知此企业与电视台达成协议,要求电视台每周至少播放6min广告,而电视台每周只能为该企业提供不多于320min的节目时间。如果你是电视台的制片人,电视台每周应播映两套连续剧各多少次,才能获得最高的收视率?
课外活动:
1. 给出平面区域如图1,若使目标函数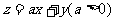 取得最大值的最优解有无穷多个,则
取得最大值的最优解有无穷多个,则 的值为___________。
的值为___________。
3.体会数学知识形成过程中所蕴涵的数学思想和方法
重点:求线性目标函数的最值问题
难点:求线性目标函数的最值问题
教 学 过 程 设 计
 活动1:1)若
活动1:1)若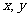 满足条件
满足条件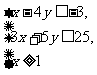 求
求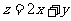 的最大值与最小值。
的最大值与最小值。
2)满足线性约束条件 的可行域中整点可行解为_______________________。
的可行域中整点可行解为_______________________。
3) 你能说出解决线性规划问题的步骤吗?
活动2:营养学家指出,成人良好的日常饮食应该至少提供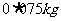 的碳水化合物,
的碳水化合物,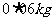 的蛋白质,
的蛋白质,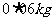 脂肪。1kg食物A含有
脂肪。1kg食物A含有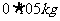 碳水化合物,
碳水化合物,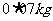 蛋白质,脂肪,花费28元;1kg食物B含有
蛋白质,脂肪,花费28元;1kg食物B含有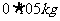 碳水化合物,
碳水化合物,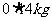 蛋白质,
蛋白质,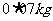 脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同
脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同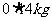 时使花费最低,需要同时食用食物A和食物B多少kg?
时使花费最低,需要同时食用食物A和食物B多少kg?
问题1.你能根据已知数据列表分析吗?
问题2:怎样解决此实际问题?
解:设___________________________________________________________
(线性约束条件是)
_____________________________________________
(目标函数是) _________________________
作出可行域(如下所示):
(找出最优解)__________________________________________________
答:
活动3:某工厂生产甲、乙两种产品,其产量分别为45个与55个,所用原料分别为A、B两种规格的金属板,每张面积分别为2m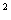 与3m
与3m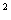 。用A种规格的金属板可造甲种产品3个,乙种产品5个;用B种规格的金属板可造甲、乙两种产品各6个。问A、B两种规格的金属板各取多少张,才能完成计划,并使总的用料面积最省?
。用A种规格的金属板可造甲种产品3个,乙种产品5个;用B种规格的金属板可造甲、乙两种产品各6个。问A、B两种规格的金属板各取多少张,才能完成计划,并使总的用料面积最省?
活动4:课内练习
2.能借助几何直观解决一些简单的线性规划问题
5、城市和城市化问题 巴西利亚 圣保罗 里约热内罗
例题1:读图填空
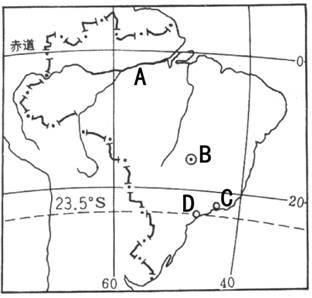
A________________(河流)该河流域有世界上最大的平原______________________。
B________________(首都)该城位于世界上最大的高原________________________。
C________________(城市)
4、热带雨林的危机 雨林破坏的原因 产生的后果
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com