
2.已知向量 =(3,1),
=(3,1), =(2k-1,k),
=(2k-1,k), ⊥
⊥ ,则k的值是
( )
,则k的值是
( )
A.-1
B. C.-
C.- D.
D.

1.若 ,则
,则 是
( )
是
( )
A. B.
B. C.
C. D.
D.
若把等式或不等式进行合理的变形后,能非常容易地画出等号或不等号两边函数的图象,则可以通过画图直接判断得出结果。尤其对于选择题、填空题这种方法更显方便、快捷。
 例10 (07安徽理科3)若对任意
例10 (07安徽理科3)若对任意 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
(A) 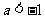 (B)
(B)  (C)
(C) 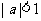 (D)
(D)
解析:对
 ,不等式
,不等式 恒成立
恒成立
则由一次函数性质及图像知 ,即
,即 。
。
上述例子剖析了近三年数学高考中恒成立问题的题型及解法,值得一提的是,各种类型各种方法并不是完全孤立的,虽然方法表现的不同,但其实质却都与求函数的最值是等价的,这也正体现了数学中的“统一美”。
利用分离参数法来确定不等式 ,(
,(  ,
, 为实参数)恒成立中参数
为实参数)恒成立中参数 的取值范围的基本步骤:
的取值范围的基本步骤:
(1) 将参数与变量分离,即化为 (或
(或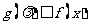 )恒成立的形式;
)恒成立的形式;
(2) 求 在
在 上的最大(或最小)值;
上的最大(或最小)值;
(3) 解不等式 (或
(或 ) ,得
) ,得 的取值范围。
的取值范围。
适用题型:(1) 参数与变量能分离;(2) 函数的最值易求出。
例8 (07年山东卷文15)当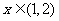 时,不等式
时,不等式 恒成立,则
恒成立,则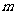 的取值范围是 .
的取值范围是 .
解析: 当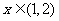 时,由
时,由 得
得 .令
.令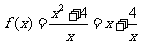 ,则易知
,则易知 在
在 上是减函数,所以
上是减函数,所以 时
时 ,则
,则 ∴
∴ .
.
例9(09年山东卷文21) 已知函数
已知函数 ,其中
,其中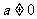 w.w.w.k.s.5…。
w.w.w.k.s.5…。
(1) 当 满足什么条件时,
满足什么条件时, 取得极值?
取得极值?
(2) 已知 ,且
,且 在区间
在区间 上单调递增,试用
上单调递增,试用 表示出
表示出 的取值范围.
的取值范围.
分析:此题虽有三个变量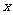 、
、 、
、 ,而
,而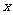 的范围已知,最终要用
的范围已知,最终要用 表示出
表示出 的取值范围,所以可以将
的取值范围,所以可以将 看成一个已知数,对
看成一个已知数,对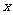 和
和 进行离参。
进行离参。
解析:(2)  在区间
在区间 上单调递增
上单调递增
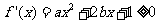 在
在 上恒成立
上恒成立
 恒成立
恒成立
 ,
, 。设
。设 ,
, ,令
,令 得
得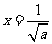 或
或 (舍去),
(舍去),
当 时,
时, ,当
,当 时
时 ,
, 单调增函数;
单调增函数;
当 时
时 ,
, 单调减函数,
单调减函数,


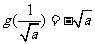 。
。
 。
。
当 时,
时, ,此时
,此时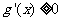 在区间
在区间 恒成立,所以
恒成立,所以 在区间
在区间 上单调递增,
上单调递增,

 ,
,
 。
。
综上,当 时,
时,  ; 当
; 当 时,
时, 。
。
某些含参不等式恒成立问题,在分离参数会遇到讨论的麻烦或者即使能容易分离出参数与变量,但函数的最值却难以求出时,可考虑变换思维角度。即把主元与参数换个位置,再结合其它知识,往往会取得出奇制胜的效果。
例6(07辽宁卷文科22)已知函数 ,
, ,且对任意的实数
,且对任意的实数  均有
均有 ,
, .
.
(Ⅰ) 求函数 的解析式;
的解析式;
(Ⅱ)若对任意的 ,恒有
,恒有 ,求
,求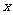 的取值范围.
的取值范围.
解析: (Ⅰ)  ,
,
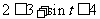 ,而
,而 ,
, 恒成立.则由二次函数性质得
恒成立.则由二次函数性质得 ,解得
,解得 ,
, ,
,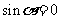

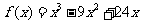 。
。
(Ⅱ) .令
.令 ,则
,则 即
即 .由于
.由于 ,则有
,则有 . 解得
. 解得  .所以
.所以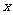 的取值范围为
的取值范围为 。
。
例7 (08安徽文科20).已知函数 ,其中
,其中 为实数.
为实数.
(Ⅱ)已知不等式 对任意
对任意 都成立,求实数
都成立,求实数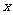 的取值范围.(节选)
的取值范围.(节选)
分析:已知参数 的范围,要求自变量
的范围,要求自变量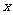 的范围,转换主参元
的范围,转换主参元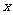 和
和 的位置,构造以
的位置,构造以 为自变量
为自变量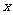 作为参数的一次函数
作为参数的一次函数 ,转换成
,转换成
 ,
,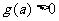 恒成立再求解。
恒成立再求解。
解析:由题设知“ 对
对
 都成立,即
都成立,即 对
对
 都成立。设
都成立。设 (
( ),
),
则 是一个以
是一个以 为自变量的一次函数。
为自变量的一次函数。 恒成立,则对
恒成立,则对
 ,
, 为
为 上的单调递增函数。 所以对
上的单调递增函数。 所以对
 ,
,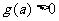 恒成立的充分必要条件是
恒成立的充分必要条件是 ,
, ,
,
 ,于是
,于是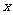 的取值范围是
的取值范围是 。
。
2、其它函数:
 恒成立
恒成立
 (注:若
(注:若 的最小值不存在,则
的最小值不存在,则 恒成立
恒成立
 的下界大于0);
的下界大于0); 恒成立
恒成立
 (注:若
(注:若 的最大值不存在,则
的最大值不存在,则 恒成立
恒成立
 的上界小于0).
的上界小于0).
例3(07年重庆卷理20)已知函数 在
在 处取得极值
处取得极值 ,其中
,其中 、
、 为常数.
为常数.
(1)试确定 、
、 的值;
的值;
(2)讨论函数 的单调区间;
的单调区间;
(3)若对任意 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。
分析:  恒成立,即
恒成立,即  ,要解决此题关键是求
,要解决此题关键是求 ,
, 。
。
解:(1)(2)略
(3)由(2)知, 在
在 处取得极小值
处取得极小值 ,此极小值也是最小值.
,此极小值也是最小值.
要使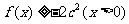 恒成立,只需
恒成立,只需 .即
.即 ,
,
从而 . 解得
. 解得 或
或 .
. 
 的取值范围为
的取值范围为 .
.
例4(08天津文21).设函数 ,其中
,其中 .
.
(Ⅲ)若对于任意的 ,不等式
,不等式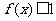 在
在 上恒成立,求
上恒成立,求 的取值范围.(节选)
的取值范围.(节选)
分析: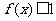 ,即
,即 ,
,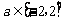 ,
,
 ,要解决此题关键是求
,要解决此题关键是求 。
。
解:(Ⅲ) 由条件
由条件 可知
可知
 ,从而
,从而 恒成立.当
恒成立.当 时,
时, ;当
;当 时,
时, .
.
因此函数 在
在 上的最大值是
上的最大值是 与
与 两者中的较大者.
两者中的较大者.
为使对任意 ,不等式
,不等式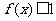 在
在 上恒成立,当且仅当
上恒成立,当且仅当 ,
,
即 ,即
,即 在
在 上恒成立.即
上恒成立.即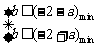 ,
,
所以 ,因此满足条件的
,因此满足条件的 的取值范围是
的取值范围是 .
.
例5(09年全国卷II文21)设函数 ,其中常数
,其中常数
(II)若当 时,
时, 恒成立,求
恒成立,求 的取值范围。(节选)
的取值范围。(节选) 

分析:利用导数求函数的最值,由恒成立条件得出不等式条件从而求出 的范围。
的范围。
解:(II)由(I)知,当 时,
时, 在
在 或
或 处取得最小值。
处取得最小值。

 ;
;
则由题意得 
 即
即 解得
解得 

 。
。
1、二次函数:
①.若二次函数 (或
(或 )在R上恒成立,则有
)在R上恒成立,则有 (或
(或 );
);
②.若二次函数 (或
(或 )在指定区间上恒成立,可以利用韦达定理以及根的分布等知识求解。
)在指定区间上恒成立,可以利用韦达定理以及根的分布等知识求解。
 例1(08年江西卷理12).已知函数
例1(08年江西卷理12).已知函数 ,若对于任一实数
,若对于任一实数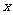 ,
, 与
与 的值至少有一个为正数,则实数
的值至少有一个为正数,则实数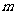 的取值范围是( )
的取值范围是( )
A.(0,2) B.(0,8) C.(2,8) D.(-∞,0)
分析: 与
与 的函数类型,直接受参数
的函数类型,直接受参数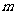 的影响,所以首先要对参
的影响,所以首先要对参
数进行分类讨论,然后转换成不等式的恒成立的问题利用函数性质及图像解题。
解析:当 时,
时, 在
在 上恒成立,而
上恒成立,而
在 上恒成立,显然不满足题意;(如图1)
上恒成立,显然不满足题意;(如图1)
当 时,
时, 在
在 上递减且
上递减且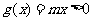 只在
只在 上恒成立,
上恒成立,
而 是一个开口向下且恒过定点(0,1)的二次函数,显然不满足题意。
是一个开口向下且恒过定点(0,1)的二次函数,显然不满足题意。
当 时,
时, 在
在 上递增且
上递增且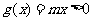 在
在 上恒成立,
上恒成立,
而 是一个开口向上且恒过定点(0,1)的二次函数,要使对任一实数
是一个开口向上且恒过定点(0,1)的二次函数,要使对任一实数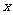 ,
,
 与
与 的值至少有一个为正数则只需
的值至少有一个为正数则只需 在
在 上恒成立。(如图3)
上恒成立。(如图3)
则有 或
或 解得
解得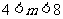 或
或 ,
,
综上可得 即
即 。 故选B。
。 故选B。
例2(09年江西卷文17)设函数 .
. 

(1)对于任意实数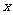 ,
, 恒成立,求
恒成立,求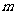 的最大值。(节选)
的最大值。(节选)
解析:(1) 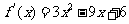 ,
,  对
对
 ,
,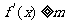 , 即
, 即 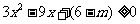 在
在 上恒成立,
上恒成立, 
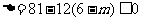 , 得
, 得 ,即
,即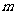 的最大值为
的最大值为 。
。
7.某运输公司有7辆可载的6t的A型卡车与4辆可载的10t的B型卡车,有9名驾驶员,建筑某段高速公路中,此公司承包了每天至少搬运360t沥青的任务,已知每辆卡车每天往返的次数为A型车8次,B型车6次,每辆卡车每天往返的成本费为A型车160元,B型车为252元,每天派出A型车和B型车各多少辆,公司所花的成本费最低?
6.某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台。已知生产这些家电产品每台所需工时和每台产值如下表:
|
家电名称 |
空调器 |
彩电 |
冰箱 |
|
工时 |
 |
 |
 |
|
产值/千元 |
4 |
3 |
2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)
5.某工厂生产甲、乙两种产品,计划每天生产量不少于15t,已知生产甲产品1t需煤9t,电力4 ,劳力3个;生产乙产品1t需煤4t,电力5
,劳力3个;生产乙产品1t需煤4t,电力5 ,劳力10个;甲产品每1t利润7万元,乙产品每1t利润12万元;但每天用煤不超过300t,电力不超过200
,劳力10个;甲产品每1t利润7万元,乙产品每1t利润12万元;但每天用煤不超过300t,电力不超过200 ,劳力只有300个。问每天各生产甲、乙两种产品多少,能使利润总额达到最大?
,劳力只有300个。问每天各生产甲、乙两种产品多少,能使利润总额达到最大?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com