
3.1999年8月,人们为有幸目睹20世纪最后一次日全食而兴奋不已的时候,英国信鸽协会的3000多名会员则十分沮丧:他们在出现日全食的一周内放出的鸽子,大多没有归巢。科学家认为,信鸽千里归巢是( )
A.靠辨别太阳的方位来导航的
B.对地形有极强的记忆力,但在日全食时无法辨别地形地貌
C.由地磁场导航,日全食干扰了地磁场的分布,从而使信鸽迷失方向
D.信鸽能发射并接收超声波而辨别方向,信鸽迷失与日全食无关,只是巧合
2.以下说法正确的是( )
A.根据E=F/q可知,在电场中某点的场强E与试探电荷电量q成反比,与其所受到的力F成正比
B.根据E=KQ/r2可知,空间某位置的场强E与产生该电场的点电荷Q的电荷量成正比
C.根据E=U/d可知,在电场中某点的场强E与两点间的距离d成反比,与这两点间的电压U成正比
D.电场中某点场强的方向与正点电荷在该点受力方向相同
1.为了防止静电的危害,下列措施中不正确的是( )
A.油罐车上拖一条与地面接触的铁链
B.在地毯中夹杂不锈钢纤维
C.飞机的机轮上装有搭地线或用导电橡胶做机轮胎
D.尽可能保持印刷厂里空气干燥
22.(本题满分14分)已知:直线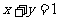 交椭圆
交椭圆 于
于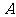 ,
,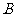 两点,且
两点,且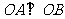 (
(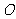 为坐标原点)
为坐标原点)
(1)求证:椭圆过定点;
(2)若椭圆的离心率在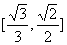 上变化时,求椭圆长轴的取值范围。
上变化时,求椭圆长轴的取值范围。
福建省福州八县(市)一中09-10学年高二上学期期末联考
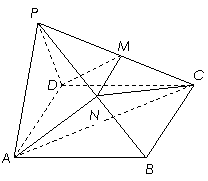
21.(本题满分12分)如图,在四棱锥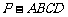 中,侧面
中,侧面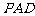 是正三角形,且与底面
是正三角形,且与底面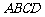 垂直,底面
垂直,底面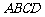 是边长为2的菱形,
是边长为2的菱形,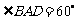 ,
,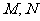 分别是
分别是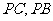 的中点。
的中点。
(1)求证: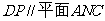 ;
;
(2)求证:平面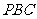 ⊥平面
⊥平面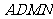 ;
;
(3)求点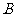 到平面
到平面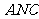 的距离
的距离

20.(本题满分12分)在平面直角坐标系中,直线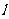 与抛物线
与抛物线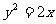 相交于
相交于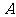 ,
,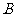 两点,
两点,
(1)求证:“如果直线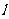 过点
过点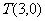 ,那么
,那么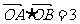 ”是真命题;
”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由。
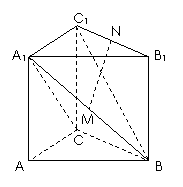
19.(本题满分12分)如图,在直三棱柱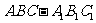 中,
中,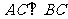 ,
, ,
,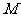 是
是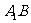 的中点,
的中点,
(1)在线段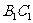 上是否存在一点
上是否存在一点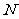 ,使得
,使得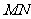 ⊥平面
⊥平面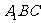 ?若存在,找出点
?若存在,找出点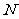 的位置幷证明;若不存在,请说明理由;
的位置幷证明;若不存在,请说明理由;
(2)求平面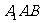 和平面
和平面 所成角的大小。
所成角的大小。

18.(本题满分12分)已知中心在原点的双曲线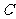 的右焦点为(2,0),右顶点为(
的右焦点为(2,0),右顶点为(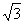 ,0)。
,0)。
(1)求双曲线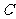 的方程;
的方程;
(2)若直线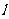 :
: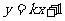 与双曲线
与双曲线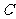 恒有两个不同的交点
恒有两个不同的交点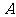 和
和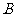 ,
,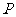 是弦
是弦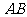 的中点,
的中点,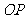 的斜率为
的斜率为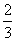 (其中
(其中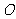 为原点),求
为原点),求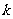 的值
的值
17.(本题满分12分)命题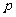 :4
:4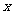 2+
2+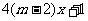 =0无实根,命题
=0无实根,命题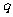 :
: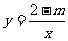 在区间(0,+
在区间(0,+ )上是减函数,若“
)上是减函数,若“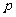 或
或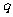 ”为真命题,求实数
”为真命题,求实数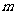 的取值范围。
的取值范围。
16.从双曲线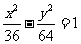 的左焦点
的左焦点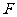 引圆
引圆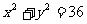 的切线,切点为
的切线,切点为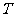 ,延长
,延长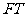 交双曲线右支于点
交双曲线右支于点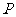 ,若
,若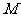 为线段
为线段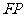 的中点,O为坐标原点,则
的中点,O为坐标原点,则 的值为
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
的值为
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com