
8.已知向量a=(1-sinθ,1),b=(,1+sinθ),且a∥b,则锐角θ等于 ( )
A.30° B.45° C.60° D.75°
解析:由a∥b可得(1-sinθ)(1+sinθ)-=0,即cosθ=±,而θ是锐角,故θ=45°.
答案:B
7.(2009·北京高考)已知向量a、b不共线,c=ka+b(k∈R),d=a-b.如果c∥d,那么( )
A.k=1且c与d同向
B.k=1且c与d反向
C.k=-1且c与d同向
D.k=-1且c与d反向
解析:不妨设a=(1,0),b=(0,1).依题意d=a-b=(1,-1),又c=ka+b=(k,1),∵c∥d,∴12-(-1)·k=0,
∴k=-1,又k=-1时,c=(-1,1)=-d,∴c与d反向.
答案:D
6.(2010·黄冈模拟)在平面直角坐标系中,O为坐标原点,设向量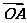 =a,
=a, =b,其中a=(3,1),b=(1,3).
=b,其中a=(3,1),b=(1,3). =λa+μb,且0≤λ≤μ≤1,C点所有可能的位置区域用阴影表正确的是
( )
=λa+μb,且0≤λ≤μ≤1,C点所有可能的位置区域用阴影表正确的是
( )

解析: =λa+μb=λ(3,1)+μ(1,3)=(3λ+μ,λ+3μ).
=λa+μb=λ(3,1)+μ(1,3)=(3λ+μ,λ+3μ).
∵0≤λ≤μ≤1,
∴0≤3λ+μ≤4,0≤λ+3μ≤4,且3λ+μ≤λ+3μ.
答案:A
|
题组三 |
平行(共线)向量的坐标表示 |
5.若α,β是一组基底,向量γ=x·α+y·β(x,y∈R),则称(x,y)为向量γ在基底α,β下的坐标,现已知向量a在基底p=(1,-1),q=(2,1)下的坐标为(-2,2),则a在另一组基底m=(-1,1),n=(1,2)下的坐标为 ( )
A.(2,0) B.(0,-2)
C.(-2,0) D.(0,2)
解析:由已知a=-2p+2q=(-2,2)+(4,2)=(2,4),
设a=λm+μn=λ(-1,1)+μ(1,2)=(-λ+μ,λ+2μ),
则由⇒,
∴a=0m+2n,∴a在基底m,n下的坐标为(0,2).
答案:D
4.在三角形ABC中,已知A(2,3),B(8,-4),点G(2,-1)在中线AD上,且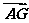 =2
=2 ,则点C的坐标是
( )
,则点C的坐标是
( )
A.(-4,2) B.(-4,-2)
C.(4,-2) D.(4,2)
解析:设C(x,y),则D(,),再由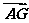 =2
=2 得(0,-4)=2(,),∴4+x=0,-2+y=-4,即C(-4,-2).
得(0,-4)=2(,),∴4+x=0,-2+y=-4,即C(-4,-2).
答案:B
3.在▱ABCD中,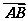 =a,
=a, =b,
=b,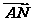 =3
=3 ,M为BC的中点,则
,M为BC的中点,则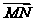 =________(用a、b表示).
=________(用a、b表示).
解析:由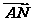 =3
=3 得4
得4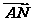 =3
=3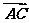 =3(a+b),
=3(a+b),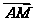 =a+b,所以
=a+b,所以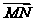 =(a+b)-(a+b)=-a+b.
=(a+b)-(a+b)=-a+b.
答案:-a+b
|
题组二 |
平面向量的坐标运算 |
2.(2010·温州模拟)已知直角坐标平面内的两个向量a=(1,3),b=(m,2m-3),使平平面内的任意一个向量c都可以唯一的表示成c=λa+μb,则m的取值范围是________.
解析:∵c可唯一表示成c=λa+μb,
∴a与b不共线,即2m-3≠3m,
∴m≠-3.
答案:{m∈R|m≠-3}
1.在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F.若
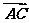 =a,
=a, =b,则
=b,则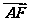 =
( )
=
( )
A.a+b B.a+b C.a+b D.a+b
 解析:如图所示,由△DEF∽△BEA知
解析:如图所示,由△DEF∽△BEA知
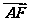 =
=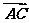 +
+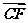 =a+
=a+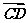
=a+(b-a)
=a+b.
答案:B
2、完成课本后面的练习1、2、3、4
★教学体会
思维方法是解决问题的灵魂,是物理教学的根本;亲自实践参与知识的发现过程是培养学生能力的关键,离开了思维方法和实践活动,物理教学就成了无源之水、无本之木。学生素质的培养就成了镜中花,水中月。
根据爱因斯坦质能方程自然界中物体的质量和能量间存在着一定对应关系:E=mc2,可见物质世界贮藏着巨大能量,问题是如何使贮藏的能量释放出来。人类以前利用的是燃料燃烧时释放的化学能。在发生化学反应时,是原子外层电子的得失,这种情况下人类获取的能量可以说属于原子的“皮能”。在核反应时,可以产生较大一些的质量亏损,从而使人类获得了大得多的能量,这里的变化属于原子核的变化,相应的能量称作原子核能。换句话说,即物体贮藏的能量是巨大的。迄今为止,人类所利用的能量还只是很小的一部分,如果人类在探索中能掌握新的方式,以产生更大的质量亏损,也就必然能够获得更为可观的能量, 这对解决人类的能源危机具有重要意义。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com