
2.了解小说《简•爱》的故事梗概及时代背景。
1.了解作者夏洛蒂•勃朗特。
4.简•爱
学习目标
4.制作一个容积为 的圆柱形容器(有底有盖),问圆柱底半径和
的圆柱形容器(有底有盖),问圆柱底半径和
高各取多少时,用料最省?(不计加工时的损耗及接缝用料)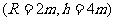
3.若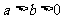 ,求证:
,求证: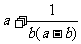 的最小值为3
的最小值为3
2.1°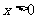 时求
时求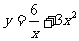 的最小值,
的最小值,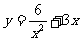 的最小值
的最小值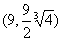
2°设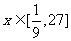 ,求
,求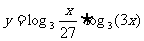 的最大值(5)
的最大值(5)
3°若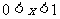 , 求
, 求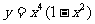 的最大值
的最大值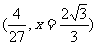
4°若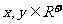 且
且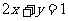 ,求
,求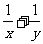 的最小值
的最小值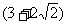
1.求下列函数的最值:
1° 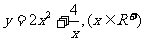 (min=6)
(min=6)
2°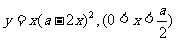 (
(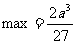 )
)
例1 求函数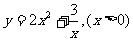 的最大值,下列解法是否正确?为什么?
的最大值,下列解法是否正确?为什么?
解一: 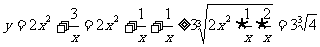 ,∴
,∴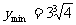
解二: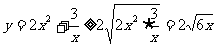 当
当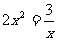 即
即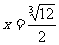 时,
时,
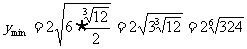

答:以上两种解法均有错误
解一错在取不到“=”,即不存在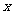 使得
使得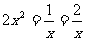 ;
;
解二错在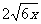 不是定值(常数)
不是定值(常数)
正确的解法是:
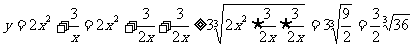
当且仅当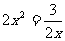 即
即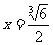 时
时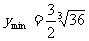

例2 若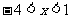 ,求
,求 的最值
的最值
解: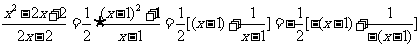
∵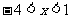 ∴
∴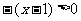
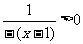
从而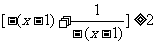
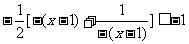
即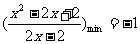

例3设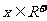 且
且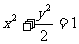 ,求
,求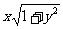 的最大值
的最大值
解:∵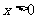 ∴
∴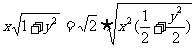

又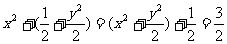 ,∴
,∴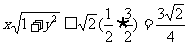

即 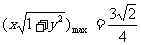

例4 已知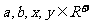 且
且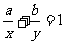 ,求
,求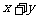 的最小值
的最小值
解: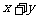
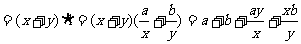
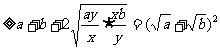

当且仅当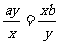 即
即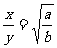 时
时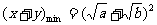

例5 将一块边长为 的正方形铁皮,剪去四个角(四个全等的正方形),作成一个无盖的铁盒,要使其容积最大,剪去的小正方形的边长为多少?最大容积是多少?
的正方形铁皮,剪去四个角(四个全等的正方形),作成一个无盖的铁盒,要使其容积最大,剪去的小正方形的边长为多少?最大容积是多少?
解:设剪去的小正方形的边长为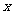 则其容积为
则其容积为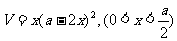

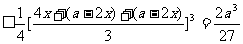
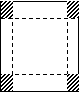 当且仅当
当且仅当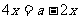 即
即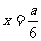 时取“=”
时取“=”
即当剪去的小正方形的边长为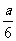 时,铁盒的容积为
时,铁盒的容积为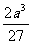

例6 已知0 < x
< 1, 0 < a < 1,试比较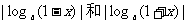 的大小
的大小
解一: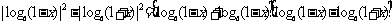
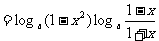

∵0 < 1 - x2 < 1, 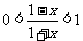 ∴
∴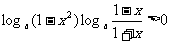
∴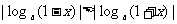

解二: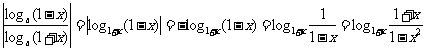
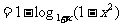

∵0 < 1 - x2 < 1, 1
+ x > 1, ∴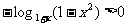
∴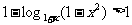 ∴
∴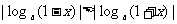

解三:∵0< x <1,∴0 < 1 - x < 1, 1< 1 + x
< 2, ∴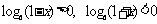
∴左 - 右
= 

∵0< 1 - x2 <1, 且0<
a <1 ∴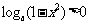 ∴
∴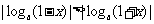

例7 已知x2 = a2 + b2,y2 = c2 + d2,且所有字母均为正,求证:xy≥ac + bd
证一:(分析法)∵a, b, c, d, x, y都是正数
∴要证:xy≥ac + bd
只需证:(xy)2≥(ac
+ bd)2
即 (a2 + b2)(c2
+ d2)≥a2c2 + b2d2 + 2abcd
展开得:a2c2 + b2d2 + a2d2
+ b2c2≥a2c2 + b2d2 + 2abcd
即 a2d2 + b2c2≥2abcd 
由基本不等式,显然成立,∴xy≥ac + bd
证二:(综合法)xy =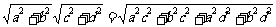
≥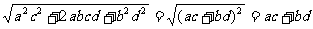

证三:(三角代换法)∵x2 = a2 + b2,∴不妨设a = xsina, b = xcosa
∵y2 = c2 + d2 ∴不妨设 c = ysinb, d
= ycosb
∴ac + bd = xysinasinb + xycosacosb = xycos(a - b)≤xy
例8 已知x1, x2均为正数,求证: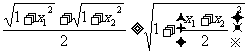
证一:(分析法)由于不等式两边均为正数,平方后只须证:
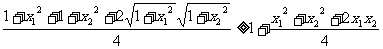

即 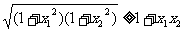

再平方 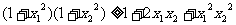

 化简整理得
化简整理得 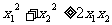 (显然成立) ∴原式成立
(显然成立) ∴原式成立
证二:(反证法)假设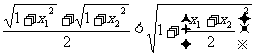
化简可得 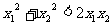 (不可能)∴原式成立
(不可能)∴原式成立
证三:(构造法)构造矩形ABCD,使AB = CD = 1, BP = x1, PC = x2
当ÐAPB = ÐDPC时,AP + PD为最短 取BC中点M,有ÐAMB = ÐDMC, BM = MC
=
取BC中点M,有ÐAMB = ÐDMC, BM = MC
=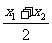 ,∴ AP + PD ≥ AM + MD
,∴ AP + PD ≥ AM + MD
即 
∴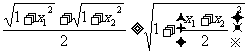
2.简述不等式证明的几种常用方法:比较、综合、分析、换元、反证、放缩、构造
1.基本不等式、极值定理;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com