
3.求简单的二面角的大小.
2.二面角的平面角的定义、作法.
1.二面角的定义、画法.
3.设 在平面
在平面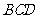 内的射影是直角三角形
内的射影是直角三角形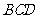 的斜边
的斜边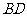 的中点
的中点 ,
,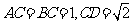 ,求(1)
,求(1) 与平面
与平面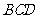 所成角的大小;(2)二面角
所成角的大小;(2)二面角 的大小;(3)异面直线
的大小;(3)异面直线 和
和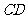 的大小
的大小
解:(1)∵ 面
面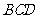 ∴
∴
∴ 为
为 与面
与面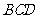 所成角
所成角
∵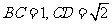 ∴
∴
∴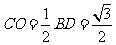 ∴
∴
 ∴
∴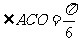
即 与平面
与平面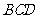 所成角的大小为
所成角的大小为

(2)取 中点
中点 ,连接
,连接 ∴
∴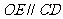
∵ ∴
∴
又∵ 面
面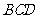 ∴
∴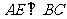
∴ 为二面角
为二面角 的平面角
的平面角
又∵
∵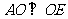 ∴
∴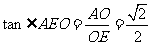 ∴
∴
即二面角 的大小为
的大小为

(3)取 的中点
的中点 ,连接
,连接 ,则
,则
∴ 与
与 所成的锐角或直角即为异面直线
所成的锐角或直角即为异面直线 和
和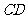 所成角
所成角
易求得

即异面直线 和
和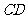 所成角为
所成角为

 1
1 ?如图所示,已知
?如图所示,已知 面
面 ,
,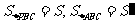 ,二面角
,二面角 的平面角为
的平面角为 ,
,
求证: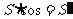
证明:过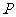 作
作 的垂线,垂足为
的垂线,垂足为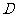 ,连接
,连接
∵ 平面
平面 ,
, 平面
平面 ,
,
∴
∴ 为二面角
为二面角 的平面角,
的平面角,
即
∵ 面
面 ∴
∴
∵ 是直角三角形 ∴
是直角三角形 ∴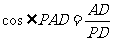
又∵
∴ ∴
∴ 即
即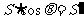
说明:这是推广的射影定理,也是求二面角平面角的一种方法
2.如图,在空间四边形 中,
中, 是正三角形,
是正三角形, 是等腰直角三角形,且
是等腰直角三角形,且 ,又二面角
,又二面角 为直二面角,求二面角
为直二面角,求二面角 的大小
的大小
 解:过
解:过 作
作 于
于
∵二面角 为直二面角 ∴
为直二面角 ∴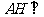 面
面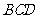
取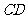 中点
中点 ,
, 为
为 中点,连接
中点,连接
∵ ∴
∴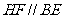
∴ ∴
∴
∴ 为二面角
为二面角 的平面角
的平面角
令 ,则
,则
∴ ∴在
∴在 中
中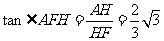
∴
即二面角 的大小为
的大小为

例1  在正四面体
在正四面体 中,求相邻两个平面所成的二面角的平面角的大小
中,求相邻两个平面所成的二面角的平面角的大小
 解:取
解:取 的中点
的中点 ,连接
,连接 ,
,
∵正四面体 ,∴
,∴ 于
于 ,
,
∴ 为二面角
为二面角 的平面角,
的平面角,
方法一:设正四面体的棱长为1,
则 ,由余弦定理得
,由余弦定理得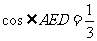
方法二:(向量运算)令 ,
, ,棱长为1,
,棱长为1,
∵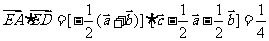 ,
,
又∵ ,∴
,∴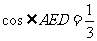
即相邻两个平面所成的二面角的平面角的大小为 .
.
例2.在棱长为1的正方体 中,
中,
(1)求二面角 的大小;
的大小;
(2)求平面 与底面
与底面 所成二面角
所成二面角 的平面角大小
的平面角大小
 解:(1)取
解:(1)取 中点
中点 ,连接
,连接 ,
,
∵正方体 ,∴
,∴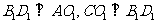 ,
,
∴ 即为二面角
即为二面角 的平面角,
的平面角,
在 中,
中,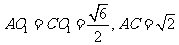 ,
,
可以求得 即二面角
即二面角 的大小为
的大小为 .
.
 (2)过
(2)过 作
作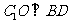 于点
于点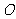 ,
,
∵正方体 ,∴
,∴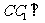 平面
平面 ,
,
∴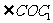 为平面
为平面 与平面
与平面 所成二面角
所成二面角 的平面角,
的平面角,
可以求得:
所以,平面 与底面
与底面 所成二面角
所成二面角 的平面角大小为
的平面角大小为 .
.
说明:求二面角的步骤:作--证--算--答
 例3.已知:二面角
例3.已知:二面角 且
且 到平面
到平面 的距离为
的距离为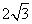 ,
, 到
到 的距离为
的距离为 ,求二面角
,求二面角 的大小
的大小
解:作 于点
于点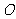 ,
, 平面
平面 于点
于点 ,连接
,连接 ,
,
∵ 于点
于点 ,
, 于点
于点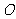 ,
,
∴ ,∴
,∴ 即为二面角
即为二面角 的平面角,
的平面角,
易知, ,
,
∴ 即二面角
即二面角 的大小为
的大小为 .
.
说明:利用三垂线定理作二面角的平面角是解决二面角问题中一种重要的方法,其特征是其中一个平面内一点作另一个平面的垂线 则已经有三种作二面角的平面角的方法,即:定义法、垂面法、三垂线法
则已经有三种作二面角的平面角的方法,即:定义法、垂面法、三垂线法
例4.如图, 平面
平面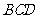 ,
, ,若
,若 ,求二面角
,求二面角 的正弦值
的正弦值
分析:要求二面角的正弦值,首先要找到二面角的平面角
解:过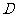 作
作 于
于 ,过
,过 作
作 交
交 于
于 ,连结
,连结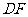 ,
,
则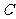 垂直于平面
垂直于平面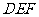 ,
,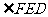 为二面角
为二面角 的平面角,
的平面角,
 ∴
∴ ,
,
又 平面
平面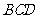 ,
,
∴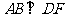 ,
, ,
,
∴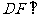 平面
平面 ,
,
∴ ,
, ,
,
又∵ ,
, ,
,
∴ 平面
平面 ,∴
,∴ ,
,
设 ,则
,则 ,
,
在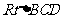 中,
中,
 ,∴
,∴ ,
,
同理,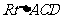 中,
中, , ∴
, ∴ ,
,
所以,二面角 的正弦值为
的正弦值为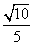 .
.
1  二面角的概念:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面
二面角的概念:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面 若棱为
若棱为 ,两个面分别为
,两个面分别为 的二面角记为
的二面角记为 ;二面角的图形表示:
;二面角的图形表示:
第一种是卧式法,也称为平卧式:


第二种是立式法,也称为直立式:


2.二面角的平面角:
(1)过二面角的棱上的一点 分别在两个半平面内作棱的两条垂线
分别在两个半平面内作棱的两条垂线 ,则
,则 叫做二面角
叫做二面角 的平面角
的平面角
(2)一个平面垂直于二面角 的棱
的棱 ,且与两半平面交线分别为
,且与两半平面交线分别为 为垂足,则
为垂足,则 也是
也是 的平面角
的平面角
说明:(1)二面角的平面角范围是 ;
;
(2)二面角的平面角为直角时,则称为直二面角,组成直二面角的两个平面互相垂直
4. 公式:已知平面a的斜线a与a内一直线b相交成θ角,且a与a相交成j1角,a在a上的射影c与b相交成j2角,则有
公式:已知平面a的斜线a与a内一直线b相交成θ角,且a与a相交成j1角,a在a上的射影c与b相交成j2角,则有 .
.
3.直线和平面所成角
(1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角
一直线垂直于平面,所成的角是直角
一直线平行于平面或在平面内,所成角为0°角.
直线和平面所成角范围:
[0, ]
]
(2)定理:斜线和平面所成角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角
1  斜线,垂线,射影
斜线,垂线,射影
 ⑴垂线 自一点向平面引垂线,垂足叫这点在这个平面上的射影. 这个点和垂足间的线段叫做这点到这个平面的垂线段.
⑴垂线 自一点向平面引垂线,垂足叫这点在这个平面上的射影. 这个点和垂足间的线段叫做这点到这个平面的垂线段.
⑵斜线 一条直线和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线 斜线和平面的交点叫斜足;斜线上一点与斜足间的线段叫这点到这个平面的斜线段
斜线和平面的交点叫斜足;斜线上一点与斜足间的线段叫这点到这个平面的斜线段
⑶射影 过斜线上斜足外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面内的射影 垂足和斜足间线段叫这点到这个平面的斜线段在这个平面内的射影
垂足和斜足间线段叫这点到这个平面的斜线段在这个平面内的射影
直线与平面平行,直线在平面由射影是一条直线 直线与平面垂直射影是点
直线与平面垂直射影是点 斜线任一点在平面内的射影一定在斜线的射影上
斜线任一点在平面内的射影一定在斜线的射影上
2.射影长相等定理:从平面外一点向这个平面所引的垂线段和斜线中
 ⑴射影相交两条斜线相交;射影较长的斜线段也较长
⑴射影相交两条斜线相交;射影较长的斜线段也较长
⑵相等的斜线段射影相等,较长的斜线段射影较长
⑶垂线段比任何一条斜线段都短
⑴OB=OCÞAB=AC OB>OCÞAB>AC
⑵AB=ACÞOB=OC AB>ACÞOB>OC
 ⑶OA<AB,OA<AC
⑶OA<AB,OA<AC
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com