
7、已知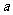 ,
,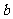 ,
, ,
,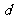 为实数,且
为实数,且 >
>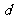 .则“
.则“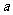 >
>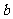 ”是“
”是“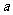 -
- >
>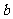 -
-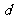 ”的
”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
[答案]B
[解析]显然,充分性不成立.又,若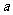 -
- >
>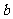 -
-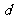 和
和 >
>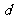 都成立,则同向不等式相加得
都成立,则同向不等式相加得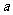 >
>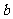
即由“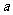 -
- >
>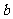 -
-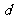 ”
” “
“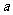 >
>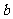 ”
”
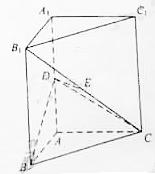
6、如图,已知六棱锥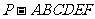 的底面是正六边形,
的底面是正六边形,

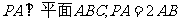 则下列结论正确的是
则下列结论正确的是
A. 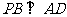
B. 
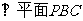
C. 直线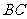 ∥
∥
D. 直线 所成的角为45°
所成的角为45°
[答案]D
[解析]∵AD与PB在平面的射影AB不垂直,所以A不成立,又,平面PAB⊥平面PAE,所以
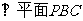 也不成立;BC∥AD∥平面PAD, ∴直线
也不成立;BC∥AD∥平面PAD, ∴直线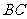 ∥
∥ 也不成立。在
也不成立。在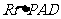 中,PA=AD=2AB,∴∠PDA=45°. ∴D正确
中,PA=AD=2AB,∴∠PDA=45°. ∴D正确
5、设矩形的长为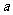 ,宽为
,宽为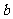 ,其比满足
,其比满足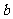 ∶
∶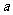 =
=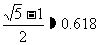 ,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是
A. 甲批次的总体平均数与标准值更接近
B. 乙批次的总体平均数与标准值更接近
C. 两个批次总体平均数与标准值接近程度相同
D. 两个批次总体平均数与标准值接近程度不能确定
[答案]A
[解析]甲批次的平均数为0.617,乙批次的平均数为0.613
[备考提示]用以上各数据与0.618(或0.6)的差进行计算,以减少
计算量,说明多思则少算。
4、已知函数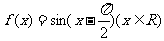 ,下面结论错误的是
,下面结论错误的是
A. 函数 的最小正周期为2
的最小正周期为2 B. 函数
B. 函数 在区间[0,
在区间[0,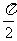 ]上是增函数
]上是增函数
C.函数 的图象关于直线
的图象关于直线 =0对称
D. 函数
=0对称
D. 函数 是奇函数
是奇函数
[答案]D
[解析]∵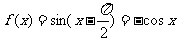 ,∴A、B、C均正确,故错误的是D
,∴A、B、C均正确,故错误的是D
[易错提醒]利用诱导公式时,出现符号错误。
3、等差数列{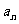 }的公差不为零,首项
}的公差不为零,首项 =1,
=1,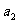 是
是 和
和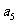 的等比中项,则数列的前10项之和是
的等比中项,则数列的前10项之和是
A. 90 B. 100 C. 145 D. 190
[答案]B
[解析]设公差为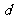 ,则
,则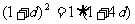 .∵
.∵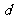 ≠0,解得
≠0,解得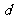 =2,∴
=2,∴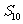 =100
=100
2、函数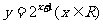 的反函数是
的反函数是
A.  B.
B.
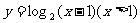
C.  D.
D.
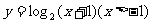
[答案]C
[解析]由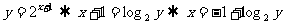 ,又因原函数的值域是
,又因原函数的值域是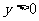 ,
,
∴其反函数是
1、设集合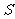 ={
={ |
| },
},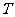 ={
={ |
|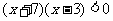 }.则
}.则 =
=
A. { |-7<
|-7< <-5 }
B. {
<-5 }
B. { | 3<
| 3< <5 }
<5 }
C. { | -5 <
| -5 < <3}
D. {
<3}
D. { | -7<
| -7< <5 }
<5 }
[答案]C
[解析]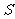 ={
={ |
|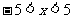 },
},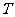 ={
={ |
|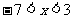 }
}
∴ ={
={ | -5 <
| -5 < <3}
<3}
17(本小题满分10分)
设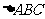 的内角
的内角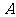 、
、 、
、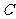 的对边长分别为
的对边长分别为 、
、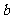 、
、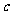 ,
, ,
,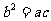 ,求
,求 。
。
分析:由 ,易想到先将
,易想到先将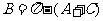 代入
代入 得
得 。然后利用两角和与差的余弦公式展开得
。然后利用两角和与差的余弦公式展开得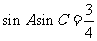 ;又由
;又由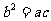 ,利用正弦定理进行边角互化,得
,利用正弦定理进行边角互化,得 ,进而得
,进而得 .故
.故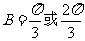 。大部分考生做到这里忽略了检验,事实上,当
。大部分考生做到这里忽略了检验,事实上,当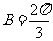 时,由
时,由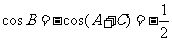 ,进而得
,进而得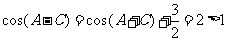 ,矛盾,应舍去。
,矛盾,应舍去。
也可利用若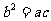 则
则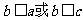 从而舍去
从而舍去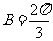 。不过这种方法学生不易想到。
。不过这种方法学生不易想到。
 评析:本小题考生得分易,但得满分难。
评析:本小题考生得分易,但得满分难。
18(本小题满分12分)
如图,直三棱柱 中,
中,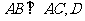 、
、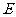 分别为
分别为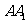 、
、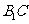 的中点,
的中点,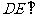 平面
平面
(I)证明:
(II)设二面角 为60°,求
为60°,求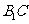 与平面
与平面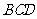 所成的角的大小。
所成的角的大小。
(I)分析一:连结BE, 为直三棱柱,
为直三棱柱, 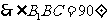
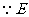 为
为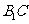 的中点,
的中点,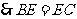 。又
。又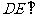 平面
平面 ,
,
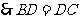 (射影相等的两条斜线段相等)而
(射影相等的两条斜线段相等)而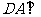 平面
平面 ,
,
 (相等的斜线段的射影相等)。
(相等的斜线段的射影相等)。
分析二:取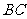 的中点
的中点 ,证四边形
,证四边形 为平行四边形,进而证
为平行四边形,进而证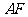 ∥
∥ ,
, ,得
,得 也可。
也可。
分析三:利用空间向量的方法。具体解法略。
(II)分析一:求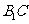 与平面
与平面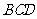 所成的线面角,只需求点
所成的线面角,只需求点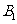 到面
到面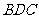 的距离即可。
的距离即可。
 作
作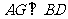 于
于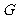 ,连
,连 ,则
,则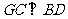 ,
,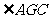 为二面角
为二面角 的平面角,
的平面角,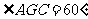 .不妨设
.不妨设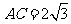 ,则
,则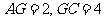 .在
.在 中,由
中,由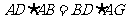 ,易得
,易得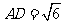 .
.
设点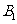 到面
到面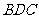 的距离为
的距离为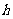 ,
,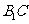 与平面
与平面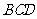 所成的角为
所成的角为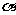 。利用
。利用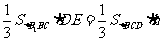 ,可求得
,可求得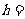
 ,又可求得
,又可求得
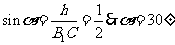
即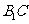 与平面
与平面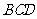 所成的角为
所成的角为
分析二:作出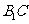 与平面
与平面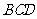 所成的角再行求解。如图可证得
所成的角再行求解。如图可证得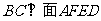 ,所以面
,所以面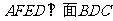 。由分析一易知:四边形
。由分析一易知:四边形 为正方形,连
为正方形,连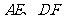 ,并设交点为
,并设交点为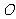 ,则
,则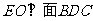 ,
,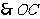 为
为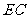 在面
在面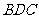 内的射影。
内的射影。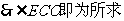 。以下略。
。以下略。
分析三:利用空间向量的方法求出面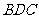 的法向量
的法向量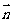 ,则
,则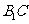 与平面
与平面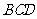 所成的角即为
所成的角即为 与法向量
与法向量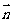 的夹角的余角。具体解法详见高考试题参考答案。
的夹角的余角。具体解法详见高考试题参考答案。
总之在目前,立体几何中的两种主要的处理方法:传统方法与向量的方法仍处于各自半壁江山的状况。命题人在这里一定会兼顾双方的利益。
19(本小题满分12分)
设数列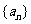 的前
的前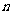 项和为
项和为 已知
已知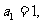
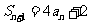
(I)设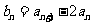 ,证明数列
,证明数列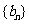 是等比数列
是等比数列
(II)求数列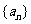 的通项公式。
的通项公式。
解:(I)由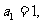 及
及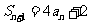 ,有
,有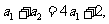

由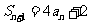 ,...① 则当
,...① 则当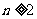 时,有
时,有 .....②
.....②
②-①得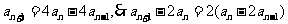
又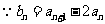 ,
,
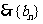 是首项
是首项 ,公比为2的等比数列.
,公比为2的等比数列.
(II)由(I)可得 ,
,
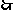 数列
数列 是首项为
是首项为 ,公差为
,公差为 的等比数列.
的等比数列.
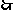
 ,
,
评析:第(I)问思路明确,只需利用已知条件寻找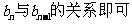 .
.
第(II)问中由(I)易得 ,这个递推式明显是一个构造新数列的模型:
,这个递推式明显是一个构造新数列的模型: ,主要的处理手段是两边除以
,主要的处理手段是两边除以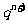 .
.
总体来说,09年高考理科数学全国I、Ⅱ这两套试题都将数列题前置,主要考查构造新数列(全国I还考查了利用错位相减法求前n项和的方法),一改往年的将数列结合不等式放缩法问题作为押轴题的命题模式。具有让考生和一线教师重视教材和基础知识、基本方法基本技能,重视两纲的导向作用。也可看出命题人在有意识降低难度和求变的良苦用心。
20(本小题满分12分)
某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(I)求从甲、乙两组各抽取的人数;
(II)求从甲组抽取的工人中恰有1名女工人的概率;
(III)记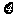 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求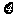 的分布列及数学期望。
的分布列及数学期望。 

分析:(I)这一问较简单,关键是把握题意,理解分层抽样的原理即可。另外要注意此分层抽样与性别无关。
(II)在第一问的基础上,这一问处理起来也并不困难。
从甲组抽取的工人中恰有1名女工人的概率
(III)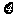 的可能取值为0,1,2,3
的可能取值为0,1,2,3
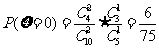 ,
,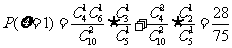 ,
,
 ,
,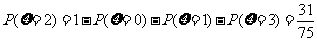
分布列及期望略。
评析:本题较常规,比08年的概率统计题要容易。在计算 时,采用分类的方法,用直接法也可,但较繁琐,考生应增强灵活变通的能力。
时,采用分类的方法,用直接法也可,但较繁琐,考生应增强灵活变通的能力。
(21)(本小题满分12分)
已知椭圆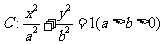 的离心率为
的离心率为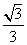 ,过右焦点F的直线
,过右焦点F的直线 与
与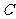 相交于
相交于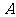 、
、 两点,当
两点,当 的斜率为1时,坐标原点
的斜率为1时,坐标原点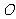 到
到 的距离为
的距离为
(I)求 ,
,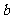 的值;
的值;
(II)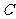 上是否存在点P,使得当
上是否存在点P,使得当 绕F转到某一位置时,有
绕F转到某一位置时,有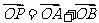 成立?
成立?
若存在,求出所有的P的坐标与 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
解:(I)设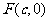 ,直线
,直线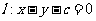 ,由坐标原点
,由坐标原点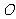 到
到 的距离为
的距离为
则 ,解得
,解得 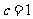 .又
.又 .
.
(II)由(I)知椭圆的方程为 .设
.设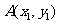 、
、
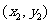
由题意知 的斜率为一定不为0,故不妨设
的斜率为一定不为0,故不妨设 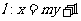
代入椭圆的方程中整理得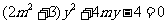 ,显然
,显然 。
。
由韦达定理有: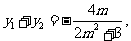
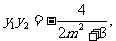 ........①
........①
.假设存在点P,使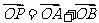 成立,则其充要条件为:
成立,则其充要条件为:
点 ,点P在椭圆上,即
,点P在椭圆上,即 。
。
整理得 。
。 

又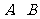 在椭圆上,即
在椭圆上,即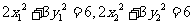 .
.
故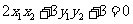 ................................②
................................②
将 及①代入②解得
及①代入②解得
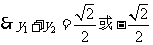 ,
, =
=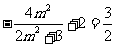 ,即
,即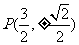 .
.
当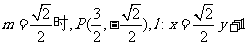 ;
;
当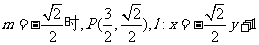 .
.
评析:处理解析几何题,学生主要是在“算”上的功夫不够。所谓“算”,主要讲的是算理和算法。算法是解决问题采用的计算的方法,而算理是采用这种算法的依据和原因,一个是表,一个是里,一个是现象,一个是本质。有时候算理和算法并不是截然区分的。例如:三角形的面积是用底乘高的一半还是用两边与夹角的正弦的一半,还是分割成几部分来算?在具体处理的时候,要根据具体问题及题意边做边调整,寻找合适的突破口和切入点。
22.(本小题满分12分)
设函数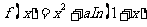 有两个极值点
有两个极值点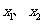 ,且
,且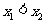
(I)求 的取值范围,并讨论
的取值范围,并讨论 的单调性;
的单调性;
(II)证明: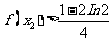
解: (I)
令 ,其对称轴为
,其对称轴为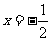 。由题意知
。由题意知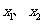 是方程
是方程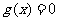 的两个均大于
的两个均大于 的不相等的实根,其充要条件为
的不相等的实根,其充要条件为 ,得
,得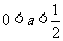
⑴当 时,
时, 在
在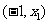 内为增函数;
内为增函数;
⑵当 时,
时,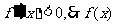 在
在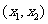 内为减函数;
内为减函数;
⑶当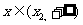 时,
时, 在
在 内为增函数;
内为增函数;
(II)由(I) ,
,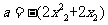

设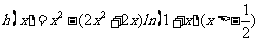 ,
,
则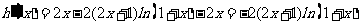
⑴当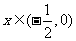 时,
时,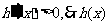 在
在 单调递增;
单调递增;
⑵当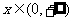 时,
时,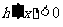 ,
,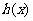 在
在 单调递减。
单调递减。
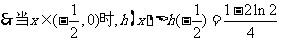
故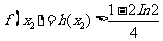 .
. 

16. 已知 为圆
为圆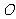 :
: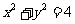 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为 ,则四边形
,则四边形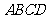 的面积的最大值为
。
的面积的最大值为
。
解:设圆心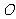 到
到 的距离分别为
的距离分别为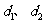 ,则
,则 .
.
四边形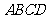 的面积
的面积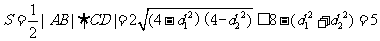
15.设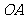 是球
是球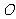 的半径,
的半径, 是
是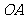 的中点,过
的中点,过 且与
且与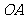 成45°角的平面截球
成45°角的平面截球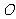 的表面得到圆
的表面得到圆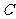 。若圆
。若圆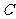 的面积等于
的面积等于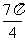 ,则球
,则球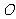 的表面积等于
的表面积等于 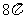 .
.
解:设球半径为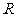 ,圆
,圆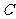 的半径为
的半径为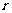 ,
,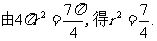
因为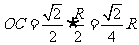 。由
。由 得
得 .故球
.故球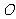 的表面积等于
的表面积等于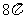 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com